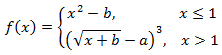Как решить систему уравнений в excel с графиком

history 8 января 2018 г.

Группы статей
• Контрольные работы и задания
• Диаграммы и графики

Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.

Пусть дана система уравнений

Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.

Видео:Решение системы нелинейных уравнений графическим способом средствами ExcelСкачать

Решение (1 ряд данных)

Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.

СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .

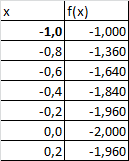
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):

Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.

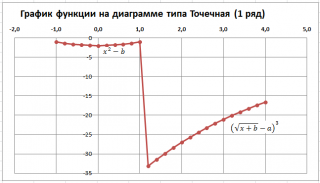
Чтобы построить диаграмму типа Точечная:

• выделите любую ячейку таблицы;
• во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .

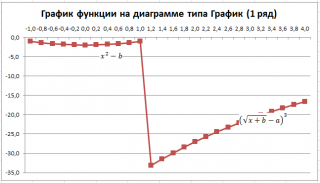
Чтобы построить диаграмму типа График:

• выделите любую столбец f(x) вместе с заголовком;
• во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .

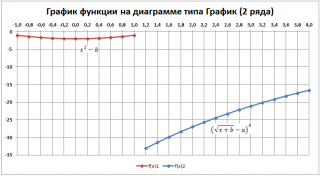
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .

Видео:Решение системы уравнений в ExcelСкачать

Решение (2 ряда данных)

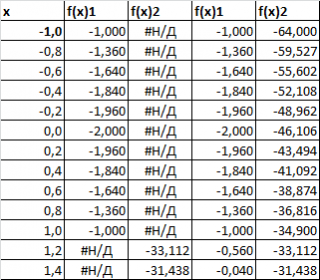
Создадим другую таблицу с исходными данными в файле примера, лист График :

Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.

У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Видео:Решение системы уравнений с двумя неизвестными помощью ExcelСкачать

Решение системы уравнений графическим методом средствами MS Excel

Цели и задачи.

1. Развитие приемов умственной деятельности, формирование и развитие функционального мышления учащихся, развитие познавательных потребностей учащихся, создание условий для приобретения опыта работы учащихся в среде ИКТ.
2. Достижение сознательного усвоения учебного материала учащимися, работа над повышением грамотности устной речи, правильного использования компьютерных терминов.
3. Научить применять возможности MS Excel в повседневной жизни, в познавательной деятельности.
4. Закрепить навыки создания таблиц и диаграмм.
5. Научить решать систему уравнений графическим методом, исследовать график функции.

Оборудование урока: компьютеры, мультимедиа проектор.

Программное обеспечение: Windows XP, пакет программ MS Office 2003.

Тема нашего урока тесно связана с математикой разделы “Графики функций” и “Решение систем уравнений”. Поэтому нам понадобятся ранее полученные навыки. Но мы постараемся упростить нашу задачу с помощью применения современных вычислительных средств.

Запишите в тетради тему урока и укажите дату.

Назовите мне кого из класса сегодня нет.

Давайте вспомним, что такое уравнение, и как его можно решить графически.

Назовите, пожалуйста, что в математике называют уравнением, решением уравнения и системой уравнений.

(Учащиеся приводят определения)

Уравнение – это математическое выражение, содержащее неизвестную величину (переменную) и 0 с правой стороны от знака =.

Система уравнений – несколько связанных уравнений, имеющих одинаковые обозначения неизвестных величин (переменных).

Решением уравнения – называют такое значение неизвестной величины, при подстановке которого левая часть выражения принимает значение 0. И мы получаем верное равенство.

Но, с другой стороны, подобное выражение можно представить как функцию с зависимой и независимой величинами. Если мы слева от знака = поставим Y, а справа заданное выражение. Y – зависимая величина, Х – независимая величина. В этом случае Решением уравнения является точка пересечения графика функции с осью ОХ.

Для решения уравнения графическим методом необходимо рассчитать значения функции в ключевых точках с координатой Х (Х меняется в диапазоне допустимых значений), нанести эти точки на систему координат, построить график функции и определить координаты точки пересечения графика с осью ОХ.

Это достаточно сложная задача. Нужно достаточно много вычислений и аккуратное построение графика функции. Также мы заранее не можем сказать, из какого диапазона чисел необходимо брать значения Х.

Но эту задачу может взять на себя ЭВМ.

Мы воспользуемся возможностями программы MS Excel.

Видео:Excel график функцииСкачать

Основная часть

Давайте разобьемся на 2 группы. Сильные ученики, которые уже хорошо владеют средствами MS Excel, попытаются самостоятельно разработать таблицу. А остальные ребята будут вместе со мной последовательно выполнять действия.

Сильные ученики пересаживаются за дальние компьютеры и самостоятельно разрабатывают таблицу для решения системы уравнений. Они должны получить примерно такую картинку на экране.

С остальными мы работаем в режиме “Делай как Я”. Я демонстрирую действия на экране проектора и комментирую, вы стараетесь выполнять эти действия у себя на ЭВМ.

И так. Мы запустили программу MS Excel.

Мы хотим разработать таблицу для решения системы уравнений:

Нам необходимо задать диапазон изменения величины Х и рассчитать соответствующее значение Y.

Сформируем начальные данные.

В ячейку A1 запишем – нач Х =. В ячейку D1 запишем – шаг Х =. В ячейках B1, E1 их соответствующие значения – (-2,5) и 0,15.

В ячейках C4, F4 запишем общий вид наших уравнений. В строке 5 сформируем заголовки будущих таблиц значений заданных функций.

Теперь в столбиках B, E мы должны сформировать значения для величины Х. А в столбиках C, E значения величин Y. У нас должна получиться вот такая картинка. Столбики со значением величины X мы должны сформировать так, чтобы было удобно менять начальное его значение и шаг X, которые мы создали в заголовке.

Формулы, которые нам нужно ввести приведены на рисунке.

Заметьте, что большинство формул повторяются, и их можно ввести методом копирования.

Заполните, пожалуйста, в каждой таблице 20-25 строчек.

Символ $ в формуле обозначает, что данный адрес ячейки является абсолютным и он не будет изменяться при копировании формулы.

Проверьте, чтобы ваши расчётные данные совпадали с рисунком 2.

Нам осталось красиво оформить таблицы. Для этого нужно указать, какие границы отображать в ячейках расположения расчётных таблиц. Выделите их указателем мышки и задайте режим “Все границы”.

Теперь нам необходимо построить графики заданных функций. Для этого воспользуемся инструментом “Диаграммы”.

Выберем тип диаграммы Точечная-Сглаженная и на следующем экране укажем необходимые нам диапазоны данных, как указано на рисунке. Незабудем указать название для каждого графика. Легенду расположим снизу. А саму диаграмму “На текущем листе”, поместив её справа от расчётных таблиц.

Если вы всё сделали правильно, то у вас на экране должна получиться вот такая картинка.

У кого не получилось, давайте вместе разберёмся в ошибках и добъёмся требуемого результата.

Теперь изменяя значения в ячейках B1, D1 можно смещать графики функций вдоль оси ОХ и изменять их масштаб.

Мы видим, что одно из решений нашей системы уравнений равно -1,5.

Изменяя начальное значение Х, найдите на графике второе решение системы уравнений.

Сколько у вас получилось?

Великолепно. У нас получилось. Мы легко решили такую сложную систему уравнений.

Но можно немного изменить нашу таблицу и усовершенствовать для решения множества подобных систем уравнений или для исследования графиков заданных функций.

Для этого нужно внести изменения в таблицу и расчётные формулы.

Можно сделать следующим образом, как показано на рисунке. Формулы в ячейках показаны на следующем рисунке.

Самостоятельно внесите все необходимые изменения.

Попробуйте изменять коофициенты A, B, C, D и посмотрите, как меняется форма и положение графиков соответствующих формул.

Видео:Решение системы уравнения с помощью настройки поиск решенияСкачать

Заключительный этап урока

Ребята, как вы думаете, что удобней самостоятельно строить график функции на бумаге или поручить эту задачу ЭВМ?

А что легче для вас?

Конечно же, на данном этапе вам удобней самостоятельно на бумаге построить график функции. Но в конце урока мы получили универсальную таблицу, которая позволяет решать множество подобных заданий.

Мы ещё раз убедились, что компьютер это мощный инструмент, который позволяет не только приятно проводить время за играми, но и решать серьёзные задачи.

Надеюсь, что вам понравилось сегодняшняя работа. И вы Довольны достигнутыми результатами.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Видео:#MicrosoftExcel Строим в Экселе график функции по системе из трёх уравненийСкачать

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

1. Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Помимо этой статьи, на сайте еще 12765 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

🔥 Видео

решаем квадратные уравнения в ExcelСкачать

Решить квадратное уравнение. MS Excel. Поиск решенияСкачать

Построение графика функции в ExcelСкачать

Графическое решение уравнений в MS Excel на одном примереСкачать

Как в excel построить графикСкачать

Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

Как построить график функции в excel | Построение графика функции в эксельСкачать

Excel для чайников Урок 9 Вложенное ЕСЛИСкачать

#MicrosoftExcel.Как в Экселе построить график функции по двум уравнениям в системеСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

MS Excel - Ввод формулСкачать