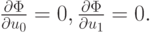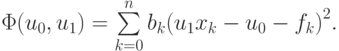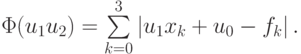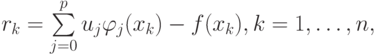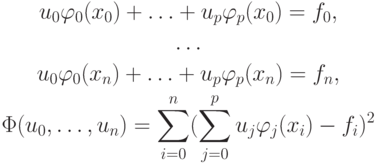Как решить переопределенную систему линейных уравнений

Видео:Матричный метод решения систем уравненийСкачать

Численное решение переопределенных СЛАУ. Метод наименьших квадратов

3.1. Пример использования метода наименьших квадратов (МНК)

Приведем простой пример получения переопределенной системы линейных уравнений. Такого рода задачи часто встречаются, например, при обработке результатов экспериментов.

Пусть f — линейная (или близкая к линейной) функция аргумента x : f(x) = u₁x + u₀ . В точках x_k известны значения функции f(x_k) . Тогда u₀, u₁ — коэффициенты , которые необходимо подобрать так, чтобы выполнялись условия u₁x_k + u₀ = f_k , k = 0,1,2,3,4, f_k = f(x_k) .

Получим систему пяти уравнений относительно двух неизвестных. Это — переопределенная система . Она не имеет классического решения, так как в общем случае не существует прямой , проходящей через все 5 точек (это возможно только тогда, когда какие — либо три уравнения полученной системы линейными преобразованиями сводятся к двум другим — система линейно зависима).

Рассмотрим общий случай. Пусть коэффициенты <u₀, u₁> необходимо определить по результатам n + 1 измерения. Введем функцию, равную сумме квадратов невязок r_k = u₁x_k + u₀ — f_k

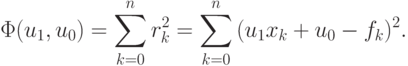( 3.1)

Примем за обобщенное решение переопределенной СЛАУ такие <u₀, u₁> для которых 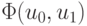принимает наименьшие значение . Для определения обобщенного решения из условия минимума суммы квадратов невязки получаем систему двух уравнений, имеющую классическое решение:

Выбор функции 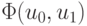имеет некоторый произвол. Например, возможно каждому измерению придать некоторый вес b_k . От набора таких весовых множителей зависело бы решение системы. В этом случае функция будет

Если в качестве невязки выбрать r_k = | u₁x_k + u₀ — f_k | , то получим задачу линейного программирования на отыскании минимума функции

Получившийся таким образом функционал, вообще говоря, не дифференцируем. Для решения задачи нельзя использовать метод наименьших квадратов .

Произвол имеется и в выборе базисных функций. Вообще говоря, можно было бы записать невязку r_k в виде

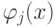
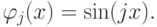
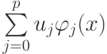
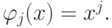
где — некоторые функции, образующие базис , например, тригонометрические: Выражение называется обобщенным полиномом. В приведенном выше примере в качестве базисных функций были выбраны степенные функции Обобщенный полином превратился в алгебраический.

В случае выбора произвольной системы базисных функций переопределенная СЛАУ и функционал 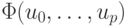будут

Отыщем обобщенное решение методом наименьших квадратов . Приравнивая все частные производные по компонентам обобщенного решения к нулю

Видео:Решение систем уравнений методом подстановкиСкачать

Как решить переопределенную систему линейных уравнений

дМС ТЕЫЕОЙС УЙУФЕНЩ МЙОЕКОЩИ БМЗЕВТБЙЮЕУЛЙИ ХТБЧОЕОЙК (мбх) ЧЙДБ AX=B , ЗДЕ A — РТСНПХЗПМШОБС НБФТЙГБ ТБЪНЕТОПУФША m УФТПЛ ОБ n УФПМВГПЧ, m>n, РТЙНЕОЕОЙЕ ОБИПДЙФ НЕФПД, ПУОПЧБООЩК ОБ SVD-ТБЪМПЦЕОЙЙ (Singular Value Decomposition) НБФТЙГЩ A :
A = U S V T
ъДЕУШ U — РТСНПХЗПМШОБС ПТФПЗПОБМШОБС РП УФПМВГБН НБФТЙГБ ТБЪНЕТОПУФША m УФТПЛ ОБ n УФПМВГПЧ, V — ЛЧБДТБФОБС ПТФПЗПОБМШОБС НБФТЙГБ ТБЪНЕТОПУФША n УФТПЛ ОБ n УФПМВГПЧ, S — ДЙБЗПОБМШОБС НБФТЙГБ ТБЪНЕТОПУФША n УФТПЛ ОБ n УФПМВГПЧ, УПДЕТЦБЭБС УЙОЗХМСТОЩЕ ЪОБЮЕОЙС НБФТЙГЩ A . рТЙЮЕН
U T U = V T V = E ,
ЗДЕ E — ЕДЙОЙЮОБС НБФТЙГБ ТБЪНЕТОПУФША n УФТПЛ ОБ n УФПМВГПЧ.

рП ОБКДЕООПНХ ТБЪМПЦЕОЙА НБФТЙГЩ A ТЕЫЕОЙЕ УЙУФЕНЩ ПРТЕДЕМСЕФУС УМЕДХАЭЙН ПВТБЪПН:
X = V diag U T B

йУИПДОЩЕ ФЕЛУФЩ ОБ СЪЩЛЕ уй РТПЗТБНН, ТЕБМЙЪХАЭЙИ SVD-ТБЪМПЦЕОЙЕ Й ТЕЫЕОЙЕ ОБ ЕЗП ВБЪЕ УЙУФЕН мбх, НПЦОП ОБКФЙ Ч МЙФЕТБФХТЕ Й Ч УПУФБЧЕ НБФЕНБФЙЮЕУЛЙИ РБЛЕФПЧ (ОБРТЙНЕТ, http://www.netlib.org/clapack ЙМЙ http://alglib.sources.ru/matrixops/general).

оЙЦЕ РТЙЧПДЙФУС РТЙНЕТ ЙУРПМШЪПЧБОЙС ДМС ТЕЫЕОЙС УЙУФЕНЩ мбх ЖХОЛГЙК ЙЪ ВЙВМЙПФЕЛЙ GSL (GNU Scientific Library).

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу ☞ ИНТЕРПОЛЯЦИЯ.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Метод наименьших квадратов

Пусть из физических соображений можно считать (предполагать), что величины $ x_ $ и $ y_ $ связаны линейной зависимостью вида $ y=kx+b $, а неизвестные коэффициенты $ k_ $ и $ b_ $ должны быть оценены экспериментально. Экспериментальные данные представляют собой $ m>1 $ точек на координатной плоскости $ (x_1,y_1), dots, (x_m,y_m) $. Если бы эти опыты производились без погрешностей, то подстановка данных в уравнение приводила бы нас к системе из $ m_ $ линейных уравнений для двух неизвестных $ k_ $ и $ b_ $: $$ y_1=k,x_1+b, dots, y_m=k,x_m+b . $$ Из любой пары уравнений этой системы можно было бы однозначно определить коэффициенты $ k_ $ и $ b_ $.

Однако, в реальной жизни опытов без погрешностей не бывает

Дорогая редакция! Формулировку закона Ома следует уточнить следующим образом:«Если использовать тщательно отобранные и безупречно подготовленные исходные материалы, то при наличии некоторого навыка из них можно сконструировать электрическую цепь, для которой измерения отношения тока к напряжению, даже если они проводятся в течение ограниченного времени, дают значения, которые после введения соответствующих поправок оказываются равными постоянной величине».

Источник: А.М.Б.Розен. Физики шутят. М.Мир.1993.

Будем предполагать, что величины $ x_,dots,x_m $ известны точно, а им соответствующие $ y_1,dots,y_m $ — приближенно. Если $ m>2 $, то при любых различных $ x_ $ и $ x_j $ пара точек $ (x_,y_i) $ и $ (x_,y_j) $ определяет прямую. Но другая пара точек определяет другую прямую, и у нас нет оснований выбрать какую-нибудь одну из всех прямых.

Часто в задаче удаленность точки от прямой измеряют не расстоянием, а разностью ординат $ k,x_i+b-y_i $, и выбирают прямую так, чтобы сумма квадратов всех таких разностей была минимальна. Коэффициенты $ k_0 $ и $ b_ $ уравнения этой прямой дают некоторое решение стоящей перед нами задачи, которое отнюдь не является решением системы линейных уравнений $$ k,x_1+b=y_1,dots, k,x_+b=y_m $$ (вообще говоря, несовместной).

Рассмотрим теперь обобщение предложенной задачи. Пусть искомая зависимость между величинами $ y_ $ и $ x_ $ полиномиальная: $$ y_1=f(x_1),dots , y_m=f(x_m), quad npu quad f(x)=a_0+a_1x+dots+a_x^ $$ Величина $ varepsilon_i=f(x_i)-y_i $ называется $ i_ $-й невязкой 1) . Уравнения $$ left<begin a_0+a_1x_1+dots+a_x_1^&=&y_1, \ a_0+a_1x_2+dots+a_x_2^&=&y_2, \ dots & & dots \ a_0+a_1x_m+dots+a_x_m^&=&y_m end right. $$ называются условными. Матрица этой системы — матрица Вандермонда (она не обязательно квадратная).

Предположим что данные интерполяционной таблицы $$ begin x & x_1 & x_2 & dots & x_m \ hline y & y_1 & y_2 &dots & y_m end $$ не являются достоверными: величины $ x_ $ нам известны практически без искажений (т.е. на входе процесса мы имеем абсолютно достоверные данные), а вот измерения величины $ y_ $ подвержены случайным (несистематическим) погрешностям.

Задача. Построить полином $ f_(x) $ такой, чтобы величина $$ sum_^m [f(x_j)-y_j]^2 $$ стала минимальной. Решение задачи в такой постановке известно как метод наименьшик квадратов 2) .

В случае $ deg f_ =m-1 $ мы возвращаемся к задаче интерполяции в ее классической постановке. Практический интерес, однако, представляет случай $ deg f_ n $: $$S=left(begin 1 &1&1&ldots&1\ x_1 &x_2&x_3&ldots&x_\ vdots&& & &vdots\ x_1^ &x_2^&x_3^&ldots&x_m^ endright) cdot left(begin 1 &x_1&x_1^2&ldots&x_1^\ 1 &x_2&x_2^2&ldots&x_2^\ ldots&& & &ldots\ 1 &x_m&x_m^2&ldots&x_m^ endright)$$ $$det S = sum_<1le j_1 0 $. По теореме Крамера система нормальных уравнений имеет единственное решение.

Осталось недоказанным утверждение, что полученное решение доставляет именно минимум сумме квадратов невязок. Этот факт следует из доказательства более общего утверждения — о псевдорешении системы линейных уравнений. Этот результат приводится ☟ НИЖЕ. ♦

Собственно минимальное значение величины cуммы квадратов невязок, а точнее усреднение по количеству узлов $$ sigma=fracsum_^m (f(x_j) -y_j)^2 $$ называется среднеквадратичным отклонением.

Показать, что линейный полином $ y=a_+a_1x $, построенный по методу наименьших квадратов, определяет на плоскости $ (x_,y) $ прямую, проходящую через центроид

Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline y & 0.35 & 0.80 & 1.70 & 1.85 & 3.51 & 1.02 end $$

Решение. Имеем $$ s_0=6, s_1=0.5 + 1 + 1.5 + 2 + 2.5 + 3=10.5, $$ $$ s_2=0.5^2 + 1^2 + 1.5^2 + 2^2 + 2.5^2 + 3^2=22.75, $$ $$t_0=0.35 + 0.80 + 1.70 + 1.85 + 3.51 + 1.02=9.23, $$ $$ t_1 =0.5cdot 0.35 + 1 cdot 0.80 + 1.5 cdot 1.70 + 2 cdot 1.85 + $$ $$ +2.5 cdot 3.51 + 3 cdot 1.02=19.06 . $$ Решаем систему нормальных уравнений $$ left( begin 6 & 10.5 \ 10.5 & 22.75 end right) left( begin a_0 \ a_1 end right)= left( begin 9.23 \ 19.06 end right), $$ 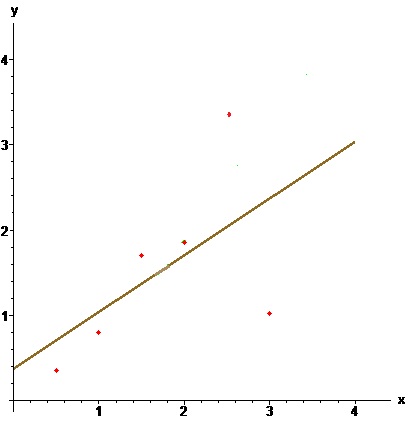получаем уравнение прямой в виде $$ y= 0.375 + 0.665, x .$$

Вычислим и полиномы более высоких степеней. $$ f_2(x)=-1.568+3.579, x-0.833,x^2 , $$ $$ f_3(x)=2.217-5.942,x+5.475,x^2-1.201, x^3 , $$ $$ f_4(x)= -4.473+17.101,x-19.320,x^2+9.205, x^3-1.487,x^4 , $$ $$ f_5(x)= 16.390-71.235,x+111.233,x^2-77.620,x^3+25.067,x^4-3.0347, x^5 . $$

Среднеквадратичные отклонения: $$ begin deg & 1 & 2 & 3 & 4 & 5 \ hline sigma & 0.717 & 0.448 & 0.204 &0.086 & 0 end $$ ♦

Возникает естественный вопрос: полином какой степени следует разыскивать в МНК? При увеличении степени точность приближения, очевидно, увеличивается. Вместе с тем, увеличивается сложность решения системы нормальных уравнений и даже при небольших степенях $ n $ (меньших $ 10 $) мы столкнемся с проблемой чувствительности решения к точности представления входных данных.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Влияние систематических ошибок

Пример. Уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы

$$ begin x & 0.5 & 1 & 1.5 & 2 & 2.5 & 3 \ hline y & 0.35 & 0.80 & 1.70 & 1.85 & 2.51 & 2.02 end $$ имеет вид (охра) $$ y=0.175+0.779, x , . $$ Теперь заменим значение $ y_5 $ на $ 0.2 $. Уравнение прямой принимает вид: $$ y=0.483+0.383, x , . $$ График (зеленый) существенно изменился. Почему это произошло? — Дело в том, что эффективность метода наименьших квадратов зависит от нескольких предположений относительно входных данных: в нашем случае — значений $ y $. Предполагается, что эти величины являлись результатами экспериментов, измерений, и, если они подвержены погрешностям, то эти погрешности носят характер несистематических флуктуаций вокруг истинных значений. Иными словами, изначально предполагается, что в действительности точки плоскости должны лежать на некоторой прямой. И только несовершенство наших методов измерений (наблюдений) демонстрирует смещение их с этой прямой. Ответ для исходной таблицы визуально подтвержает это предположение: экспериментальные точки концентрируются вокруг полученной прямой и величины невязок (отклонений по $ y $-координате) имеют «паритет» по знакам: примерно половина точек лежит выше прямой, а половина — ниже.

После замены значения $ y_5 $ на новое, значительно отличающееся от исходного, существенно меняется величина $ 5 $-й невязки $ varepsilon_5= ax_5+b-y_5 $. А поскольку в минимизируемую функцию эта невязка входи еще и в квадрате, то понятно, что изначальная прямая просто не в состоянии правильно приблизить новую точку.

Эта проблема становится актуальной в тех случаях, когда в «истинно случайный» процесс привносятся намеренные коррективы. Данные начинают подвергаться существенным искажениям, возможно, даже имеющим «злой» умысел 3) .

Как бороться с ошибками такого типа? Понятно, что решение возможно в предположении, что число таких — систематических — ошибок должно быть существенно меньшим общего количества экспериментальных данных. Понятно, что каким-то образом эти «выбросы» надо будет исключить из рассмотрения, т.е. очистить «сырые» данные от «мусора» — прежде чем подсовывать их в метод наименьших квадратов (см. ☞ цитату). Как это сделать?

Видео:Решение системы уравнений методом Крамера.Скачать

Псевдорешение системы линейных уравнений

Рассмотрим теперь обобщение задачи предыдущего пункта. В практических задачах часто бывает нужно найти решение, удовлетворяющее большому числу возможно противоречивых требований. Если такая задача сводится к системе линейных уравнений $$ left<begin a_x_1 +a_x_2+ldots+a_x_n &=&b_1\ a_x_1 +a_x_2+ldots+a_x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_m endright. iff AX= $$ при числе уравнений $ m_ $ большем числа неизвестных $ n_ $, то такая переопределенная система, как правило, несовместна. В этом случае задача может быть решена только путем выбора некоторого компромисса — все требования могут быть удовлетворены не полностью, а лишь до некоторой степени.

Псевдорешением системы $ AX= $ называется столбец $ Xin mathbb R^n $, обеспечивающий минимум величины $$ sum_^m [a_x_1 +a_x_2+ldots+a_x_n-b_i]^2 . $$

Теорема. Существует псевдорешение системы

$$ AX= $$ и оно является решением системы $$ left[A^A right]X=A^ . $$ Это решение будет единственным тогда и только тогда, когда $ operatorname A =n $.

Система $ left[A^A right]X=A^ $ называется нормальной системой по отношению к системе $ AX= $. Формально она получается домножением системы $ AX= $ слева на матрицу $ A^ $. Заметим также, что если $ m=n_ $ и $ det A ne 0 $, то псевдорешение системы совпадает с решением в традиционном смысле.

Доказательство ☞ ЗДЕСЬ.

Если нормальная система имеет бесконечное количество решений, то обычно в качестве псевдорешения берут какое-то одно из них — как правило то, у которого минимальна сумма квадратов компонент («длина»).

Пример. Найти псевдорешение системы

$$x_1+x_2 = 2, x_1-x_2 = 0, 2, x_1+x_2 = 2 .$$

Решение. Имеем: $$A=left( begin 1 & 1 \ 1 & -1 \ 2 & 1 end right), operatorname A =2, = left( begin 2 \ 0 \ 2 end right), A^A= left( begin 6 & 2 \ 2 & 3 end right), A^ = left( begin 6 \ 4 end right). $$

Ответ. $ x_1=5/7, x_2 = 6/7 $.

Показать, что матрица $ A^A $ всегда симметрична.

На дубовой колоде лежит мелкая монетка. К колоде

по очереди подходят четыре рыцаря и каждый наносит удар мечом, стараясь попасть по монетке. Все промахиваются. Расстроенные, рыцари уходят в харчевню пропивать злосчастную монетку. Укажите максимально правдоподобное ее расположение, имея перед глазами зарубки: $$ begin 3, x &- 2, y&=& 6,\ x &-3,y&=&-3,\ 11,x& + 14,y&=& 154, \ 4,x&+y&=&48. end $$

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Геометрическая интерпретация

Видео:Решение системы уравнений методом ГауссаСкачать

Псевдообратная матрица

Пусть сначала матрица $ A_ $ порядка $ mtimes n_ $ — вещественная и $ m ge n_ $ (число строк не меньше числа столбцов). Если $ operatorname (A) = n $ (столбцы матрицы линейно независимы), то псевдообратная к матрице $ A_ $ определяется как матрица $$ A^=(A^A)^ A^ . $$ Эта матрица имеет порядок $ n times m_ $. Матрица $ (A^A)^ $ существует ввиду того факта, что при условии $ operatorname (A) = n $ будет выполнено $ det (A^ A) > 0 $ (см. упражнение в пункте ☞ ТЕОРЕМА БИНЕ-КОШИ или же пункт ☞ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ ГРАМА ). Очевидно, что $ A^ cdot A = E_ $, т.е. псевдообратная матрица является левой обратной для матрицы $ A_ $. В случае $ m=n_ $ псевдообратная матрица совпадает с обратной матрицей: $ A^=A^ $.

Пример. Найти псевдообратную матрицу к матрице $$ A= left( begin 1 & 0 \ 0 & 1 \ 1 & 1 end right) . $$

Решение. $$ A^= left( begin 1 & 0 & 1 \ 0 & 1 & 1 end right) Rightarrow A^ cdot A = left( begin 2 & 1 \ 1 & 2 end right) Rightarrow $$ $$ Rightarrow (A^ cdot A)^ = left( begin 2/3 & -1/3 \ -1/3 & 2/3 end right) Rightarrow $$ $$ Rightarrow quad A^ = (A^ cdot A)^ A^ = left( begin 2/3 & -1/3 & 1/3 \ -1/3 & 2/3 & 1/3 end right) . $$ При этом $$ A^ cdot A = left( begin 1 & 0 \ 0 & 1 end right),quad A cdot A^ = left( begin 2/3 & -1/3 & 1/3 \ -1/3 & 2/3 & 1/3 \ 1/3 & 1/3 & 2/3 end right) , $$ т.е. матрица $ A^ $ не будет правой обратной для матрицы $ A_ $. ♦

Вычислить псевдообратную матрицу для $$ mathbf left( begin 1 & 0 \ 1 & 1 \ 1 & 1 end right) quad ; quad mathbf left( begin x_1 \ x_2 \ x_3 end right) . $$

Концепция псевдообратной матрицы естественным образом возникает из понятия псевдорешения системы линейных уравнений . Если $ A^ $ существует, то псевдорешение (как правило, переопределенной и несовместной!) системы уравнений $ AX=mathcal B_ $ находится по формуле $ X= A^ mathcal B $ при любом столбце $ mathcal B_ $. Верно и обратное: если $ E_, E_,dots, E_ $ – столбцы единичной матрицы $ E_m $: $$ E_=left( begin 1 \ 0 \ 0 \ vdots \ 0 end right), E_=left( begin 0 \ 1 \ 0 \ vdots \ 0 end right),dots, E_=left( begin 0 \ 0 \ 0 \ vdots \ 1 end right), $$ а псевдорешение системы уравнений $ AX=E_ $ обозначить $ X_ $ (оно существует и единственно при условии $ operatorname (A) = n $), то $$ A^=left[X_1,X_2,dots,X_m right] . $$

Теорема. Пусть $ A_ $ вещественная матрица порядка $ mtimes n_ $, $ m ge n_ $ и $ operatorname (A) = n $. Тогда псевдообратная матрица $ A^ $ является решением задачи минимизации

$$ min_<Xin mathbb R^> |AX-E_m|^2 $$ где минимум разыскивается по всем вещественным матрицам $ X_ $ порядка $ ntimes m_ $, а $ || cdot || $ означает евклидову норму матрицы (норму Фробениуса) : $$ |[h_]_|^2=sum_ h_^2 . $$ При сделанных предположениях решение задачи единственно.

С учетом этого результата понятно как распространить понятие псевдообратной матрицы на случай вещественной матрицы $ A_^ $, у которой число строк меньше числа столбцов: $ m ☞ ЗДЕСЬ

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Источники

[1]. Беклемишев Д.В. Дополнительные главы линейной алгебры. М.Наука.1983, с.187-234

🎥 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение систем уравнений методом сложенияСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы уравнений методом Крамера 2x2Скачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

Система с тремя переменнымиСкачать

Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать