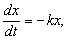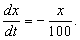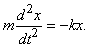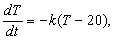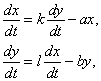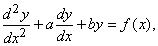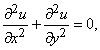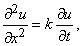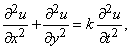Как решить нелинейное дифференциальные уравнения

Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Примеры.

Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.

1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t, то этот закон можно записать так:

где dx/dt – скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)

2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м 3 воды. Если чистая вода вливается в емкость со скоростью 1 м 3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x – количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1 м 3 раствора в емкости содержится x/100 кг соли; поэтому количество соли убывает со скоростью x/100 кг/мин, или

3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2 x/dt 2 ) пропорционально силе:

Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.

4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то

где T – температура кофе в момент времени t.

5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y – расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:

где члены —ax и —by описывают военные расходы каждой из стран, k и l – положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)

После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые «теоремы существования», в которых доказывается наличие решения у того или иного типа дифференциальных уравнений.

Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.

Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Решения дифференциальных уравнений.

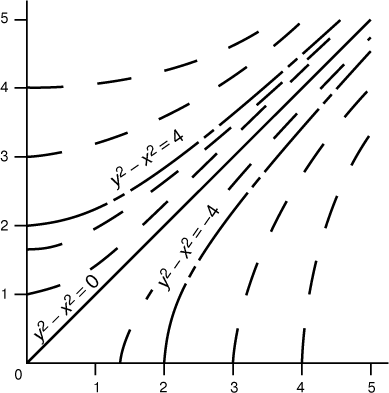
Дифференциальному уравнению, например dy/dx = x/y, удовлетворяет не число, а функция, в данном конкретном случае такая, что ее график в любой точке, например в точке с координатами (2,3), имеет касательную с угловым коэффициентом, равным отношению координат (в нашем примере 2/3). В этом нетрудно убедиться, если построить большое число точек и от каждой отложить короткий отрезок с соответствующим наклоном. Решением будет функция, график которой касается каждой своей точкой соответствующего отрезка. Если точек и отрезков достаточно много, то мы можем приближенно наметить ход кривых-решений (три такие кривые показаны на рис. 1). Существует ровно одна кривая-решение, проходящая через каждую точку с y № 0. Каждое отдельное решение называется частным решением дифференциального уравнения; если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение. Частное решение представляет собой одну функцию, в то время как общее – целое их семейство. Решить дифференциальное уравнение – это значит найти либо его частное, либо общее решение. В рассматриваемом нами примере общее решение имеет вид y 2 – x 2 = c, где c – любое число; частное решение, проходящее через точку (1,1), имеет вид y = x и получается при c = 0; частное решение, проходящее через точку (2,1), имеет вид y 2 – x 2 = 3. Условие, требующее, чтобы кривая-решение проходила, например, через точку (2,1), называется начальным условием (так как задает начальную точку на кривой-решении).

Можно показать, что в примере (1) общее решение имеет вид x = ce –kt , где c – постоянная, которую можно определить, например, указав количество вещества при t = 0. Уравнение из примера (2) – частный случай уравнения из примера (1), соответствующий k = 1/100. Начальное условие x = 10 при t = 0 дает частное решение x = 10e –t/100 . Уравнение из примера (4) имеет общее решение T = 70 + ce –kt и частное решение 70 + 130 –kt ; чтобы определить значение k, необходимы дополнительные данные.

Дифференциальное уравнение dy/dx = x/y называется уравнением первого порядка, так как содержит первую производную (порядком дифференциального уравнения принято считать порядок входящей в него самой старшей производной). У большинства (хотя и не у всех) возникающих на практике дифференциальных уравнений первого рода через каждую точку проходит только одна кривая-решение.

Существует несколько важных типов дифференциальных уравнений первого порядка, допускающих решения в виде формул, содержащих только элементарные функции – степени, экспоненты, логарифмы, синусы и косинусы и т.д. К числу таких уравнений относятся следующие.

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Уравнения с разделяющимися переменными.

Уравнения вида dy/dx = f(x)/g(y) можно решить, записав его в дифференциалах g(y)dy = f(x)dx и проинтегрировав обе части. В худшем случае решение представимо в виде интегралов от известных функций. Например, в случае уравнения dy/dx = x/y имеем f(x) = x, g(y) = y. Записав его в виде ydy = xdx и проинтегрировав, получим y 2 = x 2 + c. К уравнениям с разделяющимися переменными относятся уравнения из примеров (1), (2), (4) (их можно решить описанным выше способом).

Видео:Дифференциальные уравнения. 11 класс.Скачать

Уравнения в полных дифференциалах.

Если дифференциальное уравнение имеет вид dy/dx = M(x,y)/N(x,y), где M и N – две заданные функции, то его можно представить как M(x,y)dx – N(x,y)dy = 0. Если левая часть является дифференциалом некоторой функции F(x,y), то дифференциальное уравнение можно записать в виде dF(x,y) = 0, что эквивалентно уравнению F(x,y) = const. Таким образом, кривые-решения уравнения – это «линии постоянных уровней» функции, или геометрические места точек, удовлетворяющих уравнениям F(x,y) = c. Уравнение ydy = xdx (рис. 1) – с разделяющимися переменными, и оно же – в полных дифференциалах: чтобы убедиться в последнем, запишем его в виде ydy – xdx = 0, т.е. d(y 2 – x 2 ) = 0. Функция F(x,y) в этом случае равна (1/2)(y 2 – x 2 ); некоторые из ее линий постоянного уровня представлены на рис. 1.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейные уравнения.

Линейные уравнения – это уравнения «первой степени» – неизвестная функция и ее производные входят в такие уравнения только в первой степени. Таким образом, линейное дифференциальное уравнение первого порядка имеет вид dy/dx + p(x) = q(x), где p(x) и q(x) – функции, зависящие только от x. Его решение всегда можно записать с помощью интегралов от известных функций. Многие другие типы дифференциальных уравнений первого порядка решаются с помощью специальных приемов.

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Уравнения старших порядков.

Многие дифференциальные уравнения, с которыми сталкиваются физики, это уравнения второго порядка (т.е. уравнения, содержащие вторые производные) Таково, например, уравнение простого гармонического движения из примера (3), md 2 x/dt 2 = –kx. Вообще говоря, можно ожидать, что уравнение второго порядка имеет частные решения, удовлетворяющие двум условиям; например, можно потребовать, чтобы кривая-решение проходила через данную точку в данном направлении. В случаях, когда дифференциальное уравнение содержит некоторый параметр (число, величина которого зависит от обстоятельств), решения требуемого типа существуют только при определенных значениях этого параметра. Например, рассмотрим уравнение md 2 x/dt 2 = –kx и потребуем, чтобы y(0) = y(1) = 0. Функция y є 0 заведомо является решением, но если 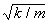– целое кратное числа p, т.е. k = m 2 n 2 p2, где n – целое число, а в действительности только в этом случае, существуют другие решения, а именно: y = sin npx. Значения параметра, при которых уравнение имеет особые решения, называются характеристическими или собственными значениями; они играют важную роль во многих задачах.

Уравнение простого гармонического движения служит примером важного класса уравнений, а именно: линейных дифференциальных уравнений с постоянными коэффициентами. Более общий пример (также второго порядка) – уравнение

где a и b – заданные постоянные, f(x) – заданная функция. Такие уравнения можно решать различными способами, например, с помощью интегрального преобразования Лапласа. То же можно сказать и о линейных уравнениях более высоких порядков с постоянными коэффициентами. Не малую роль играют также и линейные уравнения с переменными коэффициентами.

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Нелинейные дифференциальные уравнения.

Уравнения, содержащие неизвестные функции и их производные в степени выше первой или каким-либо более сложным образом, называются нелинейными. В последние годы они привлекают все большее внимание. Дело в том, что физические уравнения обычно линейны лишь в первом приближении; дальнейшее и более точное исследование, как правило, требует использования нелинейных уравнений. Кроме того, многие задачи нелинейны по своей сути. Так как решения нелинейных уравнений зачастую очень сложны и их трудно представить простыми формулами, значительная часть современной теории посвящена качественному анализу их поведения, т.е. разработке методов, позволяющих, не решая уравнения, сказать нечто существенное о характере решений в целом: например, что все они ограниченны, или имеют периодический характер, или определенным образом зависят от коэффициентов.

Приближенные решения дифференциальных уравнений могут быть найдены в численном виде, но для этого требуется много времени. С появлением быстродействующих компьютеров это время сильно сократилось, что открыло новые возможности численного решения многих, ранее не поддававшихся такому решению, задач.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Теоремы существования.

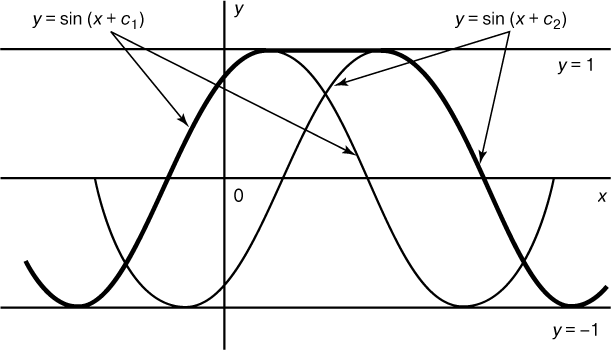
Теоремой существования называется теорема, утверждающая, что при определенных условиях данное дифференциальное уравнение имеет решение. Встречаются дифференциальные уравнения, не имеющие решений или имеющие их больше, чем ожидается. Назначение теоремы существования – убедить нас в том, что у данного уравнения действительно есть решение, а чаще всего заверить, что оно имеет ровно одно решение требуемого типа. Например, уже встречавшееся нам уравнение dy/dx = –2y имеет ровно одно решение, проходящее через каждую точку плоскости (x,y), а так как одно такое решение мы уже нашли, то тем самым полностью решили это уравнение. С другой стороны, уравнение (dy/dx) 2 = 1 – y 2 имеет много решений. Среди них прямые y = 1, y = –1 и кривые y = sin(x + c). Решение может состоять из нескольких отрезков этих прямых и кривых, переходящих друг в друга в точках касания (рис. 2).

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения в частных производных.

Обыкновенное дифференциальное уравнение – это некоторое утверждение о производной неизвестной функции одной переменной. Дифференциальное уравнение в частных производных содержит функцию двух или более переменных и производные от этой функции по крайней мере по двум различных переменным.

В физике примерами таких уравнений являются уравнение Лапласа

где, согласно одной из возможных интерпретаций, u – температура в плоской области, точки которой задаются координатами x и y; уравнение теплопроводности

где t – время, x – расстояние от одного из концов однородного стержня, по которому распространяется тепловой поток; и волновое уравнение

где t – снова время, x и y – координаты точки колеблющейся струны.

Решая дифференциальные уравнения в частных производных, обычно не стремятся найти общее решение, поскольку оно скорее всего окажется слишком общим, чтобы быть полезным. Если решение обыкновенного дифференциального уравнения определяется заданием условий в одной или нескольких точках; то решение дифференциального уравнения в частных производных обычно определяется заданием условий на одной или нескольких кривых. Например, решение уравнения Лапласа может быть найдено в точке (x, y) внутри круга, если значения u заданы в каждой точке ограничивающей окружности. Поскольку проблемы с более чем одной переменной в физике являются скорее правилом, чем исключением, легко представить, сколь обширен предмет теории дифференциальных уравнений в частных производных.

Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1982
Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1984
Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. М., 1986

Видео:"Мы зажигаем свои звёзды" О роли нелинейных дифференциальных уравненийСкачать

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

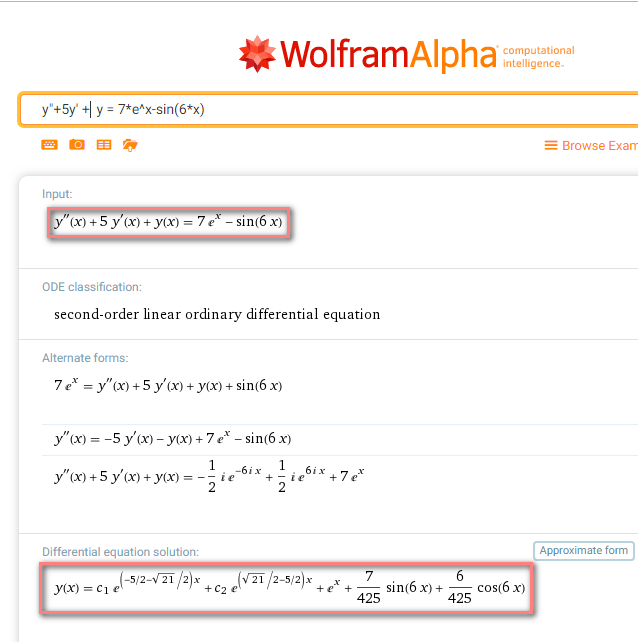
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$

Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac<9e^><3+e^>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Видео:Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

Как решить нелинейное дифференциальные уравнения

Мир математических уравнений

Точные решения > Обыкновенные дифференциальные уравнения > Нелинейные обыкновенные дифференциальные уравнения второго порядка

3. Нелинейные обыкновенные дифференциальные уравнения второго порядка

3.1. Дифференциальные уравнения вида y′′ = f(x, y)

1. y′′ = f(y). Автономное уравнение.
2. y′′ = Ax n y m . Уравнение Эмдена—Фаулера.
3. y′′ + f(x)y = ay −3 . Уравнение Ермакова.
4. y′′ = f(ay + bx + c).
5. y′′ = f(y + ax 2 + bx + c).
6. y′′ = x −1 f(yx −1 ). Однородное уравнение.
7. y′′ = x −3 f(yx −1 ).
8. y′′ = x −3/2 f(yx −1/2 ).
9. y′′ = xk−2 f(x −k y). Обобщенно-однородное уравнение.
10. y′′ = yx −2 f(x n y m ). Обобщенно-однородное уравнение.
11. y′′ = y −3 f(y(ax 2 + bx + c) −1/2 ).
12. y′′ = e −ax f(e ax y).
13. y′′ = yf(e ax y m ).
14. y′′ = x −2 f(x n e ay ).
15. y′′ = (ψ′′/ψ)y + ψ −3 f(y/ψ), ψ = ψ(x).

3.2. Дифференциальные уравнения вида f(x, y)y′′ = g(x, y, y′)

1. y′′ − y′ = f(y). Автономное уравнение.
2. y′′ + f(y)y′ + g(y) = 0. Уравнение Льенарда.
3. y′′ + [ay + f(x)]y′ + f′(x)y = 0.
4. y′′ + [2ay + f(x)]y′ + af(x)y 2 = g(x).
5. y′′ = ay′ + e 2axf(y).
6. y′′ = f(y)y′.
7. y′′ = [e αxf(y) + α]y′.
8. xy′′ = ny′ + x 2n + 1 f(y).
9. xy′′ = f(y)y′.
10. xy′′ = [x k f(y) + k − 1]y′.
11. x 2 y′′ + xy′ = f(y).
12. (ax 2 + b)y′′ + axy′ + f(y) = 0.
13. y′′ = f(y)y′ + g(x).
14. xy′′ + (n + 1)y′ = xn − 1 f(yx n ).
15. g(x)y′′ + 1/2 g′(x)y′ = f(y).
16. y′′ = −ay′ + e ax f(ye ax ).
17. xy′′ = f(x n e ay )y′.
18. x 2 y′′ + xy′ = f(x n e ay ).
19. yy′′ + (y′) 2 + f(x)yy′ + g(x) = 0.
20. yy′′ − (y′) 2 + f(x)yy′ + g(x)y 2 = 0.
21. yy′′ − n(y′) 2 + f(x)y 2 + ay 4n − 2 = 0.
22. yy′′ − n(y′) 2 + f(x)y 2 + g(x)yn + 1 = 0.
23. yy′′ + a(y′) 2 + f(x)yy′ + g(x)y 2 = 0.
24. yy′′ = f(x)(y′) 2 .
25. y′′ − a(y′) 2 + f(x)e ay + g(x) = 0.
26. y′′ − a(y′) 2 + be 4ay + f(x) = 0.
27. y′′ + a(y′) 2 − 1/2 y′ = e x f(y).
28. y′′ + α(y′) 2 = [e βxf(y) + β]y′.
29. y′′ + f(y)(y′) 2 + g(y) = 0.
30. y′′ + f(y)(y′) 2 − 1/2 y′ = e x g(y).
31. y′′ = xf(y)(y′) 3 .
32. y′′ = f(y)(y′) 2 + g(x)y′.
33. y′′ = f(x)g(xy′ − y).
34. y′′ = yx −2 f(xy′/y).
35. gy′′ + 1/2 g′y′ = f(y)h(y′g 1/2 ), g = g(x).
36. y′′ = f((y′) 2 + ay).

Веб-сайт EqWorld содержит обширную информацию о решениях различных классов обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, интегральных уравнений, функциональных уравнений и других математических уравнений.