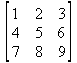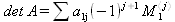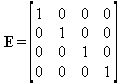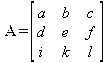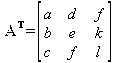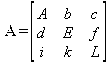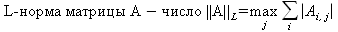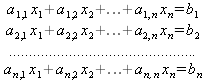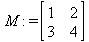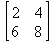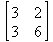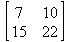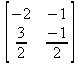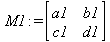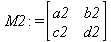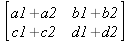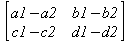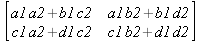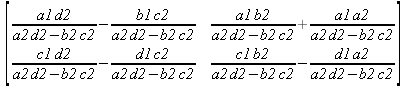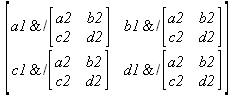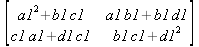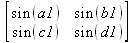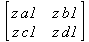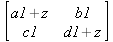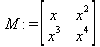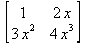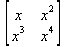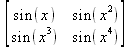Как решить матричное уравнение в maple

Видео:Решение матричных уравненийСкачать

Как решить матричное уравнение в maple

Для определения матрицы в Maple можно использовать команду matrix(n, m, [[a11,a12,…,a1n], [a21,a22,…,a2m],…, [an1,an2,…,anm]]), где n — число строк, m – число столбцов в матрице. Эти числа задавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:

В Maple матрицы специального вида можно генерировать с помощью дополнительных команд. В частности диагональную матрицу можно получить командой diag . Например:

Генерировать матрицу можно с помощью функции f ( i , j ) от переменных i , j – индексов матрицы: matrix(n, m, f), где где n — число строк, m – число столбцов. Например:

Число строк в матрице А можно определить с помощью команды rowdim(A) , а число столбцов – с помощью команды coldim(A) .

Арифметические операции с матрицами.

Сложение двух матриц одинаковой размерности осуществляется теми же командами, что и сложение векторов: evalm(A+B) или matadd(A,B). Произведение двух матриц может быть найдено с помощью двух команд:

В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например:

Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например:

Определители, миноры и алгебраические дополнения. Ранг и след матрицы.

Определитель матрицы А вычисляется командой det(A). Команда minor(A,i,j) возвращает матрицу, полученную из исходной матрицы А вычеркиванием i -ой строки и j -ого столбца. Минор M ij элемента a ij матрицы А можно вычислить командой det(minor(A,i,j)). Ранг матрицы А вычисляется командой rank(A). След матрицы А , равный сумме ее диагональных элементов, вычисляется командой trace(A). 7

Обратная и транспонированная матрицы.

Обратную матрицу А — 1 , такую что А — 1 А = АА — 1 = Е , где Е — единичная матрица, можно вычислить двумя способами:

Транспонирование матрицы А – это изменение местами строк и столбцов. Полученная в результате этого матрица называется транспонированной и обозначается А’ . Транспонированную матрицу А’ можно вычислить командой transpose(A).

Например, используя заданную в предыдущем пункте матрицу А , найдем ей обратную и транспонированную:

Выяснение типа матрицы.

Выяснить положительную или отрицательную определенность матрицы можно при помощи команды definite(A,param), где param может принимать значения: ‘positive_def’ – положительно определена ( A >0), ‘positive_semidef’ – неотрицательно определенная , ‘negative_def’ – отрицательно определенная ( A ‘negative_semidef’ — неположительно определенная . Результатом действия будет константа true – подтверждение, false – отрицание сделанного предположения. Например:

Проверить ортогональность матрицы А можно командой orthog(A).

Видео:§29 Решение матричного уравненияСкачать

Решение уравнений

Методы нахождения корней полиномов, решения уравнений, содержащих элементарные и специальные функции и систем сложных уравнений

Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Системы уравнений

Maple может решать системы линейных и нелинейных уравнений, но это хитрое дело, поскольку, чтобы разобраться в происходящем, надо рисовать уравнения, а это сложнее, так как пространство решений – многомерное.

Применяются команды solve и fsolve , но в этом случае им задаются наборы (в фигурных скобках) уравнений и переменных.

В первом примере используем solve для простой задачи линейной алгебры: John вдвое старше Kimberly. Возраст Kimberly плюс возраст John равен 27. Найти возраст каждого. Если использовать пакет LinearAlgebra, то придется рассматривать матрицу, но можно применить solve (и fsolve ), которые могут непосредственно работать с уравнениями:

Поскольку не надо беспокоиться о переводе в матричный вид, то получился иной метод решения систем линейных уравнений.

solve и fsolve можно применять для решения нелинейных систем, т. е. систем уравнений, в которых переменные – квадраты, кубы, синусы, экспоненты и т. п. Например, вот система двух нелинейных уравнений:

Вначале попробуем применить команду solve :

Maple сделал по-умному: чтобы получить уравнение для х , он исключил у из Е2 с помощью Е1 . Затем он факторизовал это квадратное уравнение, выдал ответ (x,y)=(3,4) и свел оставшуюся часть задачи к кубической. Если завершить задачу командой evalf , получим:

Но если нарисовать кубическую часть в RootOf (для оценки положения корней), то увидите, что есть еще два решения. Где же они? Примените fsolve и получите:

что еще хуже, так как дает один корень. Для поиска корней можно задавать примерно правильные числа в качестве подсказок для fsolve :

Простой способ заставить Maple дать все 4 корня: повторяйте процедуру, заменяя все целые числа на числа с плавающей точкой:

Будьте изобретательны
и пробуйте разные пути решения задачи,
возможно, один сработает.

В Maple есть другой полезный инструмент для случая двух нелинейных уравнений с двумя неизвестными. Точно так же, как в задачах с одной переменной, полезно сначала строить график, чтобы увидеть, где есть решения. В данном случае двумерные графики помогут искать корни двух неизвестных величин. Примените команду построения графиков implicitplot , которая берет уравнение с двумя переменными, вроде x 2 – y = 5, и строит определяющую их кривую в плоскости xy (для добавления команды графики надо вначале загрузить пакет графики with(plots) ):

Для графического поиска решений постройте оба уравнения на одном графике и посмотрите, где две кривые пересекают друг друга.

Из картинки ясно, что две параболы пересекаются в четырех местах, поэтому должно быть четыре решения. Окно графика должно быть достаточным, чтобы увидеть всю картинку. А если оно мало, то получится вот что:

Если у вас есть три нелинейных уравнения с тремя переменными, implicitplot3d может сделать нечто подобное (см. Maple help).

Найдите все решения (Re и Im) системы уравнений

Чтобы определить количество искомых корней, сначала постройте график с помощью implicitplot .

Вот еще нелинейная система:

Вначале попробуем solve :

(Maple на мгновение задумается, но ничего не произойдет.) Теперь попробуем fsolve с диапазонами для каждой переменной:

Похоже, что (x, y, z) = (1, 1, 3) достаточно близко к решению. Предупреждение: в трех и более измерениях Maple может ошибиться и работать, несмотря на то, что:

(a) известно, что здесь есть решение и

(b) указано, где искать приближенное значение корня.

Для лучшего понимания, где следует искать решение, можно применить implicitplot3d :

Щелкните на рисунке и покрутите его, чтобы разглядеть подробнее. После этого перерисуйте график так, чтобы он был вблизи известного решения: [x, y, z]=[1, 1, 3]:

В середине графика все три поверхности – E1 , E2 и E3 – пересекаются в точке. Это и есть то, что искали с помощью implicitplot3d , но в целом рассматривать трехмерные задачи сложно.

Пусть гладкая функция y(x) представлена тремя точками (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 ). Предположим, что эти точки определяют параболу вида y(x) = a + bx + cx 2 и что есть три аппроксимирующих уравнения для нахождения коэффициентов параболы a, b, c. Постройте эти три уравнения и используйте solve , чтобы найти формулы для a, b, c, а затем определите выражение Maple для параболы.

Задание выглядит вполне приемлемо для равноотстоящих точек. Пусть x 2 = x 1 + h и x 3 = x 1 + 2h . Упростим выражения для a, b, c. В результате получили приближенную форму функции, с которой можно работать:

(a) Оцените площадь под кривой между x 1 и x 3 путем интегрирования параболы между этими двумя пределами. Получится правило Симпсона. Чтобы посмотреть, хорош ли этот приближенный интеграл, задайте x 1 = 0, x 2 = 0.5, x 3 = 1.0 и y 1 = cos(x 1 ), y 2 = cos(x 2 ), y 3 = cos(x 3 ) , при этом приближенное значение площади будет близко к Дает ли формула приближенного интегрирования хороший результат?

(b) Оцените производную функции у(х) в средней точке х 2 путем дифференцирования параболы и вычисления значения производной в x = x 2 . Она называется формулой центральных разностей для первой производной. Проверьте ее точность при x 2 = 0.5, используя x 1 = 0.4 и x 3 = 0.6 с функцией

(c) Повторно дифференцируя формулу параболы, оцените вторую производную функции у(х) в x 2 . Это центральная вторая производная для равноотстоящих точек. Проверьте ее точность, как в части (b).

Эти формулы дифференцирования и интегрирования понадобятся в курсе физики.

Видео:Матричное уравнениеСкачать

Глава 6

Решение задач линейной алгебры, оптимизации и регрессии

Задачи линейной алгебры, оптимизации и регрессии — одни из самых массовых в науке, технике и образовании [37, 39–46]. Им и посвящена эта глава. В ней даны основные определения линейной алгебры, основы работы с массивами, векторами и матрицами, функции для работы с векторами и матрицами и для решения систем линейных уравнений. Дано описание средств оптимизации, в том числе новейших системы Maple 10.

Видео:Лекция 8. Решение матричных уравненийСкачать

6.1. Основные операции линейной алгебры

Видео:Матричный метод решения систем уравненийСкачать

6.1.1. Основные определения линейной алгебры

Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple в решении задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.

Матрица (m×n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).

Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3×3:

Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

где M₁ — определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-го столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4×4:

Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы transpose(A)∙А, где transpose(A) — транспонированная матрица А (см. ее определение ниже).

Транспонированная матрица — матрица, у которой столбцы и строки меняются местами, то есть элементы транспонированной матрицы удовлетворяют условию A T (i,j)=A(j,i). Приведем простой пример.

Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.

Диагональ матрицы — расположенные диагонально элементы А_i,i матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия поддиагоналей (элементы d и k) и наддиагоналей (элементы b и f). Матрица, все элементы которой, расположенные кроме как на диагонали, поддиагонали и наддиагонали, равны нулю, называется ленточной.

Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.

След матрицы — сумма диагональных элементов матрицы.

Матрица в целой степени — квадратная матрица в степени n (n — целое неотрицательное число), определяемая следующим образом: М 0 =Е, М 1 =М, М 2 =ММ, …, М n =М n-1 М.

Идемпотентная матрица — матрица, отвечающая условию Р²=Р.

Симметрическая матрица — матрица, отвечающая условию А т =А.

Кососимметрическая матрица — матрица, отвечающая условию А т =-А.

Ортогональная матрица — матрица, отвечающая условию А т =А -1 .

Нуль-матрица — матрица, все элементы которой равны 0.

Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы.

Комплексно-сопряженная матрица — матрица Ā, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные.

Эрмитова матрица — матрица А, удовлетворяющая условию Ā=А т .

Собственный вектор квадратной матрицы А — любой вектор х∈V n , х≠0, удовлетворяющий уравнению Ах=γх, где γ — некоторое число, называемое собственным значением матрицы А.

Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена — |А-γЕ|.

Собственные значения матрицы — корни ее характеристического многочлена.

Норма — обобщенное понятие абсолютной величины числа.

Норма трехмерного вектора ||х|| — его длина.

Норма матрицы — значение sup(||Ax||/||x||).

Матричная форма записи системы линейных уравнений — выражение А∙Х=В, где А — матрица коэффициентов системы, X — вектор неизвестных и В — вектор свободных членов. Один из способов решения такой системы очевиден — X=А -1 ∙В, где А -1 — обратная матрица.

Видео:§28 Матричные уравненияСкачать

6.1.2. Системы линейных уравнений и их матричная форма

Как известно, обычная система линейных уравнений имеет вид:

Здесь а_1,1, а_1,2, …, a_n,n — коэффициенты, образующие матрицу А и могущие иметь действительные или комплексные значения, х₁, х₂, …, х_n — неизвестные, образующие вектор X и b₁, b₂, …, b_n — свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений, X — искомый вектор неизвестных и В — вектор свободных членов. Из такого представления системы линейных уравнений вытекают различные способы ее решения: X=В/А (с применением матричного деления), X=А -1 В (с инвертированием матрицы А) и так далее.

Видео:Решение системы линейных уравнений в MapleСкачать

6.1.3. Матричные разложения

В ходе решения задач линейной алгебры часто приходится использовать различные методы, например известный еще из школы метод исключения Гаусса. Однако для эффективного решения таких задач приходится представлять матрицы специальным образом, осуществляя матричные разложения. В ходе этого приходится работать с некоторыми специальными типами матриц, что нередко резко упрощает решения систем линейных уравнений. Отметим некоторые из наиболее распространенных матричных разложений, которые реализованы в большинстве СКА и СКМ.

LU-разложение, называемое также треугольным разложением, соответствует матричному выражению вида Р∙А=L∙U, где L — нижняя и U — верхняя треугольные матрицы. Все матрицы в этом выражении квадратные.

QR-разложение имеет вид А=Q∙R, где Q — ортогональная матрица, a R — верхняя треугольная матрица. Это разложение часто используется при решении любых систем линейных уравнений, в том числе переопределенных и недоопределенных и с прямоугольной матрицей.

Разложение Холецкого А=L∙L T применяется к симметричной матрице А, при этом L — треугольная матрица.

Сингулярное разложение матрицы А размера M×N (М×N) определяется выражением А=U∙s∙VT, где U и V — ортогональные матрицы размера N×N и М×M, соответственно, a s — диагональная матрица с сингулярными числами матрицы А на диагонали.

Видео:Вычисления, константы и решение уравнений в MapleСкачать

6.1.4. Элементы векторов и матриц

Элементы векторов и матриц в Maple являются индексированными переменными, то есть место каждого элемента вектора определяется его индексом, а у матрицы — двумя индексами. Обычно их обобщенно обозначают как i (номер строки матрицы или порядковый номер элемента вектора) и j (номер столбца матрицы). Допустимы операции вызова нужного элемента и присваивания ему нового значения:

V[i] — вызов i-го элемента вектора V;

M[i,j] — вызов элемента матрицы М, расположенного на i-й строке в j-м столбце.

V[i]:=x — присваивание нового значения х i-му элементу вектора V;

M[i,j]:=x — присваивание нового значения х элементу матрицы М.

Видео:Матричные уравненияСкачать

6.1.5. Преобразование списков в векторы и матрицы

Прежде всего, надо обратить внимание на то, что векторы и матрицы, хотя и похожи на списки, но не полностью отождествляются с ними. В этом можно убедиться с помощью следующих примеров (файл vmop), в которых функция type используется для контроля типов множественных объектов (векторов и матриц):

Таким образом, используя функцию преобразования данных convert, можно преобразовывать одномерные списки в векторы, а двумерные — в матрицы. Функция type используется в следующих формах:

type(V,vector) — тестирует аргумент V и возвращает true, если V — вектор, и false в ином случае;

type(M.matrix) — тестирует аргумент М и возвращает true, если М — матрица, и false в ином случае.

Здесь параметры vector и matrix используются для указания того, какой тип объекта проверяется. Обратите внимание на то, что матрицы отображаются иначе, чем двумерные списки — без двойных квадратных скобок. Отображение вектора подобно отображению одномерного списка, поэтому здесь особенно важен контроль типов данных.

Видео:РЕШЕНИЕ ВОЛНОВОГО ДУ ОПЕРАЦИОННЫМ МЕТОДОМ В СРЕДЕ MAPLESOFT MAPLE 2017Скачать

6.1.6. Операции с векторами

Важное достоинство систем компьютерной алгебры, к которым относится и Maple, заключается в возможности выполнения аналитических (символьных) операций над векторами и матрицами. Перед проведением символьных операций с векторами и матрицами рекомендуется очистить память от предшествующих определений с помощью команды restart. Если какие-то элементы векторов или матриц были ранее определены, это может привести к очень сильным искажениям вида конечных результатов. Очистка памяти устраняет возможность ошибок такого рода.

Приведем примеры операций над векторами (файл vectop):

В этих примерах используется функция evalm(M), осуществляющая вычисление матрицы или вектора М.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

6.1.7. Операции над матрицами с численными элементами

Над матрицами с численными элементами в Maple можно выполнять разнообразные операции. Ниже приведены основные из них:

Рекомендуется внимательно изучить эти примеры и попробовать свои силы в реализации простых матричных операций.

Видео:Матричные уравненияСкачать

6.1.8. Символьные операции с матрицами

Одной из привлекательных возможностей СКА является возможность проведения символьных операций с матрицами. Ниже представлены примеры символьных операций, осуществляемых над квадратными матрицами одного размера в системе Maple:

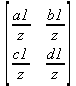
Приведем еще ряд гримеров выполнения символьных операций с одной матрицей:

Среди других функций для работы с матрицами полезно обратить внимание на функцию map, которая применяет заданную операцию (например, функции дифференцирования diff и интегрирования int) к каждому элементу матрицы. Примеры такого рода даны ниже:

В результате возвращаются матрицы, каждый элемент которых представлен производной или интегралом. Аналогично можно выполнять над матрицами и другие достаточно сложные преобразования.

В дальнейшем мы продолжим изучение матричных функций и операций, включенных в пакеты Maple.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

6.2. Пакет линейной алгебры linalg системы

Видео:Интерактивная математика в Maple 2017 | Clickable Math in Maple 2017Скачать

6.2.1. Состав пакета linalg

Несомненно, что уникальной возможностью системы Maple, как и других систем компьютерной алгебры, является возможность решения задач линейной алгебры в символьном (формульном, аналитическом) виде. Однако такое решение представляет скорее теоретический, чем практический интерес, поскольку даже при небольших размерах матриц (уже при 4–5 строках и столбцах) символьные результаты оказываются очень громоздкими и трудно обозримыми. Они полезны только при решении специфических аналитических задач, например с разреженными матрицами, у которых большинство элементов имеют нулевые значения.

Поэтому разработчики Maple были вынуждены реализовать в своей системе численные методы решения задач линейной алгебры, которые широко используются в основных сферах ее приложения — математическом моделировании систем и устройств, расчетах в электротехнике, механике, астрономии и т.д. Решение задач линейной алгебры в численном виде можно рассматривать как одну из форм визуализации результатов вычислений, относящихся к линейной алгебре.

В ядро Maple, как отмечалось, введены очень скромные и минимально необходимые средства для решения задач линейной алгебры. Основной упор в их реализации сделан на подключаемые пакеты. Основным из них, унаследованным от предшествующих реализаций системы, является пакет решения задач линейной алгебры linalg. Это один из самых обширных и мощных пакетов в области решения задач линейной алгебры. Для их просмотра достаточно использовать команду:

Для большинства пользователей системой Maple набор функций пакета оказывается чрезмерно обширным и потому опущен. Укажем, однако, наиболее употребительные функции пакета linalg:

• addcol — добавляет к одному из столбцов другой столбец, умноженный на некоторое число;

• addrow — добавляет к одной из строк другую строку, умноженную на некоторое число;

• angle — вычисляет угол между векторами;

• augment — объединяет две или больше матриц по горизонтали;

• backsub — реализует метод обратной подстановки при решении системы линейных уравнений (см. также forwardsub);

• band — создает ленточную матрицу;

• basis — находит базис векторного пространства;

• bezout — создает Bezout-матрицу двух полиномов;

• BlockDiagonal — создает блок-диагональную матрицу;

• blockmatrix — создает блок-матрицу;

• cholesky — декомпозиция Холесского для квадратной положительно определенной матрицы;

• charmat — создает характеристическую матрицу (charmat(M,v) матрица, вычисляемая как v∙E-М);

• charpoly — возвращает характеристический полином матрицы;

• colspace — вычисляет базис пространства столбцов;

• colspan — находит базис линейной оболочки столбцов матрицы;

• companion — вычисляет сопровождающую матрицу, ассоциированную с полиномом;

• cond — вычисляет число обусловленности матрицы (cond(M) есть величина norm(M)∙norm(M -l ));

• curl — вычисляет ротор вектора;

• definite — тест на положительную (отрицательную) определенность матрицы;

• diag — создает блок-диагональную матрицу;

• diverge — вычисляет дивергенцию векторной функции;

• eigenvals — вычисляет собственные значения матрицы;

• eigenvects — вычисляет собственные векторы матрицы;

• equal — определяет, являются ли две матрицы равными;

• exponential — создает экспоненциальную матрицу;

• ffgausselim — свободное от дробей Гауссово исключение в матрице;

• fibonacci — матрица Фибоначчи;

• forwardsub — реализует метод прямой подстановки при решении системы линейных уравнений (например для матрицы L и вектора b forwardsub(L,b) возвращает вектор решения х системы линейных уравнений L∙x=b);

• frobenius — вычисляет форму Фробениуса (Frobenius) матрицы;

• gausselim — Гауссово исключение в матрице;

• gaussjord — синоним для rref (метод исключения Гаусса-Жордана);

• geneqns — генерирует элементы матрицы из уравнений;

• genmatrix — генерирует матрицу из коэффициентов уравнений;

• grad — градиент векторного выражения;

• GramSchmidt — вычисляет ортогональные векторы;

• hadamard — вычисляет ограничение на коэффициенты детерминанта;

• hessian — вычисляет гессиан-матрицу выражения;

• hilbert — создает матрицу Гильберта;

• htranspose — находит эрмитову транспонированную матрицу;

• ihermite — целочисленная эрмитова нормальная форма;

• indexfunc — определяет функцию индексации массива;

• innerprod — вычисляет векторное произведение;

• intbasis — определяет базис пересечения пространств;

• ismith — целочисленная нормальная форма Шмитта;

• iszero — проверяет является ли матрица ноль-матрицей;

• jacobian — вычисляет якобиан векторной функции;

• JordanBlock — возвращает блок-матрицу Жордана;

• kernel — находит базис ядра преобразования, соответствующего данной матрице;

• laplacian — вычисляет лапласиан;

• leastsqrs — решение уравнений по методу наименьших квадратов;

• linsolve — решение линейных уравнений;

• Ludecomp — осуществляет LU-разложение;

• minpoly — вычисляет минимальный полином матрицы;

• mulcol — умножает столбец матрицы на заданное выражение;

• mulrow — умножает строку матрицы на заданное выражение;

• multiply — перемножение матриц или матрицы и вектора;

• normalize — нормализация вектора;

• orthog — тест на ортогональность матрицы;

• permanent — вычисляет перманент матрицы — определитель, вычисляемый без перестановок;

• pivot — вращение относительно элементов матрицы;

• potential — вычисляет потенциал векторного поля;

• Qrdecomp — осуществляет QR-разложение;

• randmatrix — генерирует случайные матрицы;

• randvector — генерирует случайные векторы;

• ratform — вычисляет рациональную каноническую форму;

• references — выводит список основополагающих работ по линейной алгебре;

• rowspace — вычисляет базис пространства строки;

• rowspan — вычисляет векторы охвата для места столбца;

• rref — реализует преобразование Гаусса-Жордана матрицы;

• scalarmul — умножение матрицы или вектора на заданное выражение;

• singval — вычисляет сингулярное значение квадратной матрицы;

• singularvals — возвращает список сингулярных значений квадратной матрицы;

• smith — вычисляет Шмиттову нормальную форму матрицы;

• submatrix — извлекает указанную подматрицу из матрицы;

• subvector — извлекает указанный вектор из матрицы;

• sumbasis — определяет базис объединения системы векторов;

• swapcol — меняет местами два столбца в матрице;

• swaprow — меняет местами две строки в матрице;

• sylvester — создает матрицу Сильвестра из двух полиномов;

• toeplitz — создает матрицу Теплица;

• trace — возвращает след матрицы;

• vandermonde — создает вандермондову матрицу;

• vecpotent — вычисляет векторный потенциал;

• vectdim — определяет размерность вектора;

• wronskian — вронскиан векторных функций.

Назначение многих функция вполне очевидно из названия. Далее мы рассмотрим более подробно некоторые функции из этого пакета. С деталями синтаксиса (достаточно разнообразного) для каждой из указанных функций можно ознакомиться в справочной системе Maple. Для этого достаточно использовать команду ?name;, где name — имя функции (из приведенного списка).

Видео:Графики, функции, решение системы линейных уравнений в MapleСкачать

6.2.2. Интерактивный ввод матриц

Для интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix:

После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид:

📺 Видео

Решение системы уравнений методом обратной матрицы.Скачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать