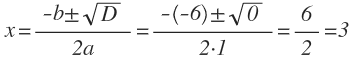Как решить квадратное уравнение если корень из дискриминанта не извлекается

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Видео:Что делать если корни не извлекаются? #shortsСкачать

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Если D>0, то уравнение имеет два различных

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Видео:Что делать если корни не извлекаются? #егэ2024 #егэматематика #огэ #огэ2024 #огэматематикаСкачать

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Данное уравнение является квадратным. Но в его условии присутствует квадратный корень, что усложняет нам задачу для нахождения его корней, в том плане, что необходимо увидеть, какие же ограничения на переменную х здесь будут.

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного корня): ограничение на х: 5 − х ≥ 0

Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

х 2 − 2 х − 24 = 0

Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:ЛОВИ ПРОДОЛЖЕНИЕ 😉 ДИСКРИМИНАТ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Как извлекать квадратный корень без калькулятора, даже если он не извлекается нацелоСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Что делать когда дискриминант не извлекается из под корня?

Алгебра | 5 — 9 классы

Что делать когда дискриминант не извлекается из под корня?

Пример такой : Х = 7 + / — (21 под корнем) / 2.

Если Дискриминант не извлекается из под корня.

То корни уравнения так и записываются.

Видео:Быстрый способ решения квадратного уравненияСкачать

Формулы дискриминанта и корней?

Формулы дискриминанта и корней.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

5x = 3x ^ 2 найти дискриминант и корни?

5x = 3x ^ 2 найти дискриминант и корни.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Найдите дискриминант и корни 6х² — 11х — 1 = 0?

Найдите дискриминант и корни 6х² — 11х — 1 = 0.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Найдите дискриминант и корни?

Найдите дискриминант и корни.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Найдите ошибку, дискриминант 573 получается, а корень не извлекается?

Найдите ошибку, дискриминант 573 получается, а корень не извлекается.

Как такие корни извлекать?

Видео:ОТРИЦАТЕЛЬНЫЙ ДИСКРИМИНАНТ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

При каких значениях дискриминанта D квадратное уравнение не имеет корней?

При каких значениях дискриминанта D квадратное уравнение не имеет корней.

Видео:Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

Пожалуйста решите уравнение 3x ^ 2 — 2 — 5 = 0 никак не могу найти дискриминант ?

Пожалуйста решите уравнение 3x ^ 2 — 2 — 5 = 0 никак не могу найти дискриминант ?

Из — под корня не извлекается.

Видео:Отрицательный дискриминантСкачать

Здравствуйте, помогите пожалуйста?

Здравствуйте, помогите пожалуйста.

Что делать если корень не извлекается из дискриминанта, пример числа 128.

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Дайте определение тождества?

Дайте определение тождества.

Что называют дискриминантом квадратного уравнения?

Сколько корней может иметь квадратное уравнение?

Если вам необходимо получить ответ на вопрос Что делать когда дискриминант не извлекается из под корня?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Алгебра вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

А) если х = 0. 75, то (5х — 1) — (2 — 8х) = 5х — 1 — 2 + 8х = 13х — 3 = 13 * 0. 75 — 3 = 9. 75 — 3 = 6. 75 в) 12 + 7х — (1 — 3х) если х = — 0. 7, то 12 + 7х — 1 + 3х = 11 + 10х = 11 + 10 * ( — 0. 7) = 11 — 7 + 4 (если, что так под буквой в, нап..

5х — 1) — (2 — 8х) = 5х — 1 — 2 + 8х = 13х — 3 при х = 0, 75 13 * 0, 75 — 3 = 9, 75 — 3 = 6, 75 Ответ : 6, 75.

На первой полке 3х книг на второй х книг когда переставили 32 книги на первой полке стало 3х — 32 на второй полке стало х + 32 х + 32 = 3х — 32 2х = 64 х = 32 на второй на первой 16 * 3 = 96 книг.

Пусть на второй полке было — х книг, тогда на первой было — 3х книг после того как книги переставили на второй полке стало книг — х + 32 а на первой стало книг — 3х — 32 зная, что книг стало поровну (по условию) получим уравнение : 3х — 32 = х + 32 3..

🎦 Видео

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать