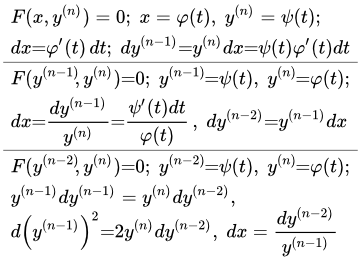Как решить дифференциальное квадратное уравнение

Здесь рассмотрены методы решения дифференциальных уравнений высших порядков, решаемые в квадратурах, то есть решения которых можно выразить через конечное число интегралов. К таким уравнениям относятся следующие типы:
⇓
⇓
⇓
Также приводятся подробно разобранные примеры решений ⇓ таких уравнений.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

F(x, y (n) ) = 0: Дифференциальные уравнения, содержащее только независимую переменную и производную n-го порядка

Рассмотрим дифференциальное уравнение высшего порядка, содержащее только независимую переменную x и производную n-го порядка :
(1) .

y (n) = f(x) Разрешенные относительно старшей производной

Если уравнение (1) удастся разрешить относительно производной, то есть представить в виде
(1.1) ,
то оно решается непосредственным интегрированием.

x = f(y (n) ) Разрешенные относительно независимой переменной

Рассмотрим случай, когда уравнение (1) можно разрешить относительно переменной x . В этом случае, независимая переменная является функцией от старшей производной:
(1.2.1) .
Это уравнение можно решить в квадратурах в параметрическом виде, последовательно понижая порядок.

Вводим параметр t :
(1.2.2) .
Тогда из (1.2.1) получаем:
(1.2.3) .
При переходе к параметрическому виду (1.2.2) – (1.2.3), независимой переменной становится параметр t , а переменные и x – зависимыми от параметра t .

Возьмем дифференциал от (1.2.3):
;
(1.2.4) .
Выразим производную n-го порядка через производную порядка n–1 , воспользовавшись уравнением:
.
Учитывая (1.2.2), и подставляя (1.2.4), находим выражение дифференциала производной n–1 — го порядка через параметр t :
.

Интегрируя, получаем выражение производной n-1 — го порядка через параметр t :
(1.2.5) .
Это уравнение, вместе с (1.2.3), дает выражение производной меньшего порядка в параметрическом виде:

Далее выражаем дифференциал производной порядка n – 2 :
.
Подставляя (1.2.4) и (1.2.5), получаем дифференциал, выраженный через параметр t . После чего интегрируем по t , и, вместе с уравнением , получаем выражение производной в параметрическом виде. И так далее, пока получим зависимость функции y от параметра t .

F(x, y (n) ) = 0 Общий случай

Теперь рассмотрим дифференциальное уравнение высшего порядка, содержащее только старшую производную и независимую переменную в общем случае:
(1.3.1) .
Это уравнение можно разрешить в квадратурах, если удастся представить уравнение (1.3.1) в параметрическом виде. То есть если удастся подобрать такие функции , для которых
(1.3.2) ,
и при этом уравнение (1.3.1) окажется эквивалентным уравнениям
(1.3.3) .

Тогда уравнение можно решить в квадратурах. Для этого сначала выразим дифференциал независимой переменной x через параметр t , используя первое уравнение (1.3.3):
.
После этого выражаем через параметр t дифференциал производной n-1-го порядка:
.
Интегрируя это уравнение по переменной t , получаем выражение для производной n-1-го порядка в параметрическом виде:
.
Где .

Далее выражаем через t дифференциал производной n-2-го порядка:
.
Интегрируя, получим параметрическое представление производной n-2-го порядка. И так далее, пока получим параметрическое представление функции y .

Видео:Дифференциальные уравнения. 11 класс.Скачать

F(y (n-1) , y (n) ) = 0 Уравнения, содержащие только производные порядков n и n-1

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
(2.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(2.1.2) .
Тогда если положить
(2.1.3) ,
то уравнение (2.1.1) будет выполняться автоматически. При этом должно соблюдаться еще одно условие – чтобы представления (2.1.1) и (2.1.3) были эквивалентными. То есть, чтобы при переходе от одного представления к другому, не появились новые и не терялись существующие решения.

Если найдено такое параметрическое представление уравнения (2.1.1), то его можно решить в квадратурах. Для этого, как и в предыдущем случае, сначала выразим дифференциал независимой переменной x через параметр t . Преобразуем первое уравнение (2.1.3):
.
Отсюда
;
(2.1.4) .
Интегрируя, получаем выражение независимой переменной x через параметр t :
(2.1.5) .

Тем же способом, что и в предыдущем случае, выражаем производные и меньших порядков через t :
.
Интегрируем:
.
Продолжая процесс, получаем выражения остальных производных и самой функции y через параметр t . Вместе с уравнением (2.1.5), это дает решение исходного уравнения в параметрическом виде.

y (n-1) = f(y (n) ) Разрешенные относительно младшей производной

Рассмотрим частный случай уравнения (2.1.1), в котором производная меньшего порядка выражена через старшую производную:
.

Это уравнение интегрируется в квадратурах, введением параметра
.
Тогда
.
Из этих уравнений
;
;
;
.

Тем же способом находим выражение через t производных и переменной y .

y (n) = f(y (n-1) ) Разрешенные относительно старшей производной

Рассмотрим второй частный случай, когда старшая производная выражена через производную меньшего порядка:
(2.3.1) .

Если уравнение (2.3.3) удастся разрешить относительно t , то получим зависимость вида . Учитывая (2.3.2), получаем уравнение, в котором производная n–1-го порядка является функцией от независимой переменной:
.
Интегрируя это уравнение n–1 раз, получим зависимость y от x . См. Дифференциальное уравнение y (n) = f(x)

Но в любом случае можно получить решение в параметрическом виде.
;
.

Тем же способом находим выражение через t производных и переменной y .

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

F(y (n-2) , y (n) ) = 0 Уравнения, содержащие только производные порядков n и n-2

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
(3.1.1) .
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
(3.1.2) .
Положим
(3.1.3) .
Тогда уравнение (3.1.1) выполняется автоматически. Считаем также, что представления (3.1.1) и (3.1.3) эквивалентны.

Для решения уравнения запишем дифференциалы производных порядков n-1 и n-2 :
.
Исключаем dx . Из второго уравнения
(3.1.4) .
Подставим в первое и преобразуем:
;
;
.
Подставляя (3.1.3) и интегрируя, получим выражение производной через параметр t :
;
;
;
.
Знак плюс или минус выбирается из начальных условий, как и постоянная интегрирования .

Из (3.1.4) находим выражение x через t :
(3.1.5) ;
(3.1.6) .

Далее, как и в предыдущих случаях находим выражения производных и зависимой переменной y через t . Например,
;
;
и так далее.

Примечание. В литературе иногда не ставят знак плюс-минус. При этом подразумевают, что корень является многозначной функцией и автоматически может быть как положительным, так и отрицательным.

y (n) = f(y (n-2) ) Разрешенные относительно старшей производной

Сведем к квадратурам уравнение, разрешенное относительно старшей производной:
(3.2.1) .

Для упрощения выкладок введем новую переменную:
(3.2.2) .
Тогда исходное уравнение (3.2.1) станет уравнением второго порядка:
(3.2.3) .
Умножим его на и выделим полную производную:
;
.
Отсюда получаем первый интеграл:
.

Находим выражение для дифференциала . Для этого извлекаем квадратный корень:
.
Отсюда
(3.2.4) .
Знак плюс или минус выбирается из начальных условий. В общем решении допустим любой знак.

Интегрируя, получаем зависимость u от x в неявном виде:
(3.2.5) .
Если после интегрирования удастся разрешить u относительно x , то, поскольку , мы получим уравнение вида (1.1), которое решается последовательным интегрированием.

Если уравнение (3.2.5) разрешить относительно u не удастся, то решаем в параметрическом виде, как это описывалось ранее. То есть вводим параметр . Тогда (3.2.5) и (3.2.4) дают выражения переменной x и ее дифференциала через t :
(3.2.6) .
(3.2.7) .
Далее, уравнение

вместе с (3.2.7) дают параметрическое представление зависимости производной порядка n — 2 от переменной x .

Используя (3.2.6), можно найти параметрическое представление остальных производных и самой функции y от переменной x . Например,
;
.
И так далее.

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Примеры решений задач

Все примеры Далее рассматриваются примеры с подробными решениями следующих дифференциальных уравнений.
⇓
⇓
⇓
⇓
⇓

Пример 1

Найти общее решение дифференциального уравнения третьего порядка, содержащего только старшую производную и независимую переменную.
(П1.1) .

По всей видимости, в уравнении (П1.1) выразить через x в элементарных функциях или не возможно, или довольно сложно. Мы не будем пытаться это делать, поскольку здесь независимая переменная x выражена через производную . Поэтому решаем задачу в параметрическом виде.

Вводим параметр t . Получаем параметрические уравнения, эквивалентные (П1.1):
(П1.2) .

Выразим дифференциал переменной x через параметр t :
;
(П1.3) .

Используя (П1.2) и (П1.3), выражаем дифференциал производной второго порядка через параметр t :
.
Интегрируем.
;
(П1.4) .

Используя (П1.3) и (П1.4), аналогично предыдущему имеем:

;

.

Пример 2

Найти частное решение дифференциального уравнения второго порядка, содержащее только вторую производную и независимую переменную:
(П2.1) ;
(П2.2) .

Это уравнение является кубическим по отношению ко второй производной , и уравнением седьмой степени (если умножить его на x ) по отношению к независимой переменной x . Можно попытаться разрешить его относительно или x , но здесь есть более простой способ.

Заметим, что уравнение (П2.1) выполняется, если выразить зависимость от x , определяемую уравнением (П2.1) в параметрическом виде:
(П2.3) .
Действительно, подставляя (П2.3) в (П2.1) получаем:
;
;
.
То есть если взять параметрическое представление (П2.3), то уравнение (П2.1) выполняется.

Однако это не означает, что представление (П2.3) автоматически эквивалентно уравнению (П2.1). Поскольку кубическое уравнение может иметь три действительных корня, то, возможно, уравнение (П2.3) можно представить в параметрическом виде тремя неэквивалентными способами. Также возможен случай, когда условия теоремы существования и единственности решения дифференциального уравнения не выполняются, и заданным начальным условиям будут удовлетворять несколько решений. Все это нужно иметь в виду при решении подобных уравнений. Но нам нужно найти любое решение, удовлетворяющее заданным начальным условиям. Поэтому попробуем применить для этой цели представление (П2.3).

Выразим дифференциал независимой переменной x через дифференциал параметра t , используя (П2.3):
.
Выразим дифференциал производной через параметр t и его дифференциал:
.
Интегрируем:
. Найдем значение постоянной , используя первое начальное условие (П2.2). Из (П2.3) находим: . При . При . Отсюда .

Итак, мы нашли параметрическое представление для производной:
.
Аналогично предыдущему, выражаем y через параметр t :
;

.
Находим значение постоянной , используя второе начальное условие (П2.2). При . При . Отсюда .

Тем самым мы нашли частное решение в параметрическом виде:
.
Выразим t через x .
;
.

Пример 3

Решить дифференциальное уравнение, содержащее только производные первого и второго порядков:
(П3.1) .

Нетрудно видеть, что если положить
(П3.2) ,
то уравнение (П3.1) выполняется автоматически. Поэтому решаем это уравнение в параметрическом виде.

Выразим дифференциал независимой переменной x через параметр t .
;
;
(П3.3) .

Интегрируя (П3.3), получаем выражение независимой переменной x через параметр t :
;
(П3.4) .

Используя формулу , и применяя выражение через t (см. (П3.2)), выразим дифференциал dy через t :
.

Интегрируя, находим выражение зависимой переменной через параметр t :
.

Итак, мы нашли зависимость в параметрической форме:
.
Отсюда можно получить зависимость y от x в явном виде. Из второго уравнения, . Подставляем в первое:
.

Пример 4

Решить дифференциальное уравнение, содержащее только производные второго и третьего порядков:
(П4.1) .

Это дифференциальное уравнение содержит только производные второго и третьего порядков. При этом оно разрешено относительно высшей производной. Решаем параметрическим методом. За параметр t возьмем производную второго порядка:
(П4.2) .

Выразим дифференциал независимой переменной x через параметр t . Из (П4.1) имеем:
;
;
(П4.3) .

Выразим независимую переменную x через параметр t . Для этого интегрируем (П4.3):
;
(П4.4) .
См. Обратные гиперболические функции, их графики и формулы

Выразим дифференциал через параметр t и, интегрируя, выразим производную через t :
;
;
(П4.5) .

Выразим дифференциал зависимой переменной y через параметр t . После чего интегрируя, выразим y через t :
;
;
(П4.6) .

Исключим параметр t из уравнений (П4.4) т (П4.6).
;
.

Примечание.
Эту задачу можно решить проще, если с самого начала выбрать следующее параметрическое представление для производных:
.

Пример 5

Решить дифференциальное уравнение с заданными начальными условиями:
(П5.1) ;
(П5.2) .

Уравнение имеет вид (3.2.3). В нем вторая производная выражена через функцию (зависимую переменную y ). Решаем изложенным выше методом ⇑.

Умножим исходное уравнение (П5.1) на и выделяем полный дифференциал.
;
;
;
.
Извлекаем квадратный корень:
(П5.3) .

Найдем значение постоянной и знак корня из начальных условий (П5.2). Для этого подставляем в (П5.3) :
.
Отсюда видно, что нужно взять знак плюс и . Тогда
.

Разделяем переменные и интегрируем.
;
;
;
(П5.4) .

Определяем значение постоянной . Для этого подставляем значения начальных условий (П5.2): :
.
Отсюда . Подставляем в (П5.4):
.

Возводим в квадрат и выполняем преобразования:
;
.
Извлекаем квадратный корень:
.
Выбираем знак плюс или минус из начальных условий (П5.2). Подставляем :
.
Этому уравнению удовлетворяет знак плюс. Тогда
.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 11-05-2021

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Видео:Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях

Линейным дифференциальным уравнением второго порядка называется уравнение вида

где y — функция, которую требуется найти, а p(x) , q(x) и f(x) — непрерывные функции на некотором интервале (a, b) .

Если правая часть уравнения равна нулю ( f(x) = 0 ), то уравнение называется линейным однородным уравнением. Таким уравнениям и будет в основном посвящена практическая часть этого урока. Если же правая часть уравнения не равна нулю ( f(x) ≠ 0 ), то уравнение называется линейным неоднородным уравнением (смотрите отдельный урок).

В задачах от нас требуется разрешить уравнение относительно y» :

Линейные дифференциальные уравнения второго порядка имеют единственное решение задачи Коши.

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Линейное однородное дифференциальное уравнение второго порядка и его решение

Рассмотрим линейное однородное дифференциальное уравнение второго порядка:

Если y 1 (x) и y 2 (x) — частные решения этого уравнения, то верны следующие высказывания:

1) y 1 (x) + y 2 (x) — также является решением этого уравнения;

2) Cy 1 (x) , где C — произвольная постоянная (константа), также является решением этого уравнения.

Из этих двух высказываний следует, что функция

также является решением этого уравнения.

Возникает справедливый вопрос: не является ли это решение общим решением линейного однородного дифференциального уравнения второго порядка, то есть таким решением, в котором при различных значениях C 1 и C 2 можно получить все возможные решения уравнения?

Ответ на этот вопрос следуюший: может, но при некотором условии. Это условие о том, какими свойствами должны обладать частные решения y 1 (x) и y 2 (x) .

И это условие называется условием линейной независимости частных решений.

Теорема. Функция C 1 y 1 (x) + C 2 y 2 (x) является общим решением линейного однородного дифференциального уравнения второго порядка, если функции y 1 (x) и y 2 (x) линейно независимы.

Определение. Функции y 1 (x) и y 2 (x) называются линейно независимыми, если их отношение является константой, отличной от нуля:

Однако установить по определению, являются ли эти функции линейно независимыми, часто очень трудоёмко. Существует способ установления линейной независимости с помощью определителя Вронского W(x) :

.

Если определитель Вронского не равен нулю, то решения — линейно независимые. Если определитель Вронского равен нулю, то решения — линейно зависимымые.

Пример 1. Найти общее решение линейного однородного дифференциального уравнения .

Решение. Интегрируем дважды и, как легко заметить, чтобы разность второй производной функции и самой функции была равна нулю, решения должны быть связаны с экспонентой, производная которой равна ей самой. То есть частными решениями являются и .

Так как определитель Вронского

не равен нулю, то эти решения линейно независимы. Следовательно, общее решение данного уравнения можно записать в виде

.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

где p и q — постоянные величины.

На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность — нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины.

Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида

которое, как видно, является обычным квадратным уравнением.

В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Для полной определённости будем считать, что все частные решения прошли проверку определителем Вронского и он во всех случаях не равен нулю. Сомневающиеся, впрочем, могут проверить это самостоятельно.

Корни характеристического уравнения — действительные и различные

Иными словами, . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Пример 2. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет вид , его корни и — вещественные и различные. Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

.

Пример 3. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет вид , его корни и — вещественные и различные. Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

.

Корни характеристического уравения — вещественные и равные

То есть, . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Пример 4. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет равные корни . Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

Пример 5. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет равные корни . Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

.

Корни характеристического уравнения — комплексные

То есть, , , . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Пример 6. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет комплексные корни и . Соответственно и . Общее решение данного дифференциального уравения имеет вид

.

Пример 7. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет комплексные корни и . Соответственно и . Общее решение данного дифференциального уравения имеет вид

.

Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение

Пример 8. Решить линейное однородное дифференциальное уравнение

.

Пример 9. Решить линейное однородное дифференциальное уравнение

.

📹 Видео

4. Однородные дифференциальные уравнения (часть 1)Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать