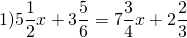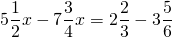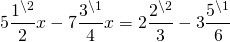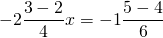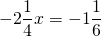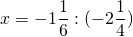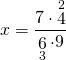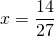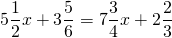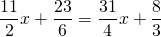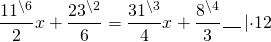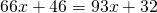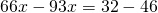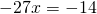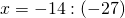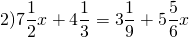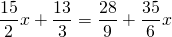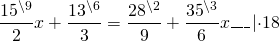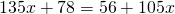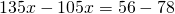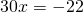Как решаются уравнения с смешанными дробями (6 видео)

Уравнения со смешанными дробями

Уравнения со смешанными дробями можно решать двумя способами. Рассмотрим каждый из них на примере.

Решить уравнение со смешанными дробями:

1 способ: Это — линейное уравнение . Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Смешанные числа переведем в неправильные дроби:

Теперь обе части уравнения умножаем на наименьший общий знаменатель всех входящих в него дробей:

Таким образом, уравнение со смешанными дробями заменили на уравнение с целыми числами:

Это — линейные уравнения. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Ответ записываем в виде обыкновенной дроби:

Решать уравнения со смешанными числами можно обоими способами. На мой взгляд, второй способ удобнее. Еще два уравнения со смешанными дробями, решенные с помощью умножения на наименьший общий знаменатель.

Переводим смешанные числа в неправильные дроби:

Обе части уравнения умножаем на наименьший общий знаменатель всех дробей:

От уравнения со смешанными числами переходим к уравнению с целыми числами:

неизвестные слагаемые переносим в одну сторону, известные — в другую, изменяя при переносе знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Содержание

Решение уравнений с дробями
Понятие дроби
Основные свойства дробей
Понятие уравнения
Понятие дробного уравнения
Как решать уравнения с дробями
1. Метод пропорции
2. Метод избавления от дробей
Что еще важно учитывать при решении
Универсальный алгоритм решения
Примеры решения дробных уравнений
Математика. 6 класс
🔍 Видео

Видео:Уравнения с дробями 6 класс (задания, примеры) - как решать?Скачать

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Видео:Уравнение с дробями видео урок ( Математика 5 класс )Скачать

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:МАТЕМАТИКА 5 КЛАСС: РЕШЕНИЕ УРАВНЕНИЙ СО СМЕШАННЫМИ ЧИСЛАМИСкачать

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = −b : а;
если а равно нулю, а b не равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Квадратное уравнение выглядит так:

ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Видео:Уравнение со смешанными дробямиСкачать

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:КАК РЕШАТЬ УРАВНЕНИЯ СО СМЕШАННЫМИ ЧИСЛАМИ, ДРОБЯМИ И СКОБКАМИ? Примеры | МАТЕМАТИКА 5 классСкачать

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка;
умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение;
делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Уравнения с дробями 5 класс (задания, примеры) - как решать?Скачать

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2.
Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

Видео:СМЕШАННЫЕ ДРОБИ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Математика. 6 класс

Конспект урока

Обобщение и систематизация знаний по теме «Смешанные дроби. Уравнения»

Перечень рассматриваемых вопросов:

– сложение, вычитание, умножение и деление смешанных дробей с разными знаками;

– уравнения, корни уравнения;

– уравнение как перевод условия задачи на математический язык;

– решение задач с помощью уравнений.

Натуральные числа – это числа, которые используются при подсчёте предметов.

Правильная дробь – это дробь, у которой числитель меньше знаменателя.

Положительная смешанная дробь есть сумма натурального числа и правильной дроби.

Уравнение – это равенство, содержащее букву, значение которой надо найти.

Решить уравнение – это значит найти все его корни.

Корнем уравнения называют такое число, при подстановке которого в уравнение вместо неизвестного получают верное числовое равенство.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

«Учение – путь к умению!» –гласит известная поговорка. Сегодня мы будем учиться решать уравнения со смешанными дробями. Для этого сегодня мы повторим действия сложения, умножения, вычитания и деления смешанных дробей.

Для начала вспомним правило сложения (вычитания) смешанных дробей.

Чтобы сложить (вычесть) смешанные дроби, надо:

1) отдельно сложить (вычесть) их целые части;

2) отдельно сложить (вычесть) дробные части.

Если дроби с разными знаменателями, то нужно их привести к общему знаменателю.

При этом необходимо помнить, что дроби складываются, если они с одинаковыми знаками, при этом знак дробей сохраняется. Если дроби с разными знаками, то они вычитаются. Из большего модуля вычтем меньший и перед разностью поставим знак слагаемого с большим модулем. При необходимости из целой части уменьшаемого занимают единицу и переводят её в дробную часть.

А теперь вспомним правило умножения смешанных дробей.

Сначала переводим смешанные дроби в неправильные. Затем выполняем вычисления с дробями: определяем знак результата и выполняем действия с модулями (с положительными дробями), находим произведение отдельно числителей и отдельно знаменателей. Произведение числителей пишем числителем новой дроби, а произведение знаменателей, знаменателем новой дроби. При необходимости упрощаем результат: сокращаем дробь и выделяем её целую часть.

При выборе знака произведения используем следующее правило. Если количество отрицательных множителей чётное, то произведение будет положительным, если количество отрицательных множителей нечётное, то знак произведения будет отрицательным.

Чётное число множителей со знаком «–» → Результат со знаком «+»

Нечётное число множителей со знаком «–» → Результат со знаком «–»

Вспомним общий алгоритм деления смешанных дробей.

Сначала переводим смешанную дробь в неправильную.

Затем переводим деление в умножение, переворачивая вторую дробь, т.е. умножаем делимое на число обратное делителю. И находим произведение числителей и знаменателей. Это будут соответственно числитель и знаменатель новой дроби. При необходимости упрощаем результат: сокращаем дробь и выделяем её целую часть.

При выборе знака частного используем такое же правило, как и при умножении. Если количество отрицательных дробей чётное, то частное будет положительным, если количество отрицательных дробей нечётное, то знак частного будет отрицательным.

Все арифметические действия можно использовать при решении уравнений и задач, которые сводятся к уравнениям. Напомним алгоритм решения задач с помощью уравнений.

Во-первых, неизвестную величину нужно обозначить буквой.

Во-вторых, используя условие задачи, составить уравнение.

Затем решить это уравнение.

И ответить на вопрос задачи.

Решая уравнение, мы можем использовать следующие приёмы:

– переносить числа из одной части уравнения в другую, меняя знак числа на противоположный;

– делить или умножать обе части уравнения на одно и то же отличное от нуля число.

Задача на движение

Путь от пункта А до пункта В у мотоциклиста занимает 30 мин, а у велосипедиста – 2 часа. Скорость мотоциклиста на 42 км/ч больше скорости велосипедиста. С какой скоростью движется велосипедист?

Обозначим через х км/ч скорость велосипедиста и сведём известные и неизвестные величины в таблицу.

Тогда скорость мотоциклиста (х + 42) км/ч.

Путь велосипедиста 2х км.

Расстояние, пройденное мотоциклистом и велосипедистом – одинаковое.

Умножим левую и правую часть уравнения на 2:

Перенесём х в правую часть с противоположным знаком:

Разделим обе части уравнения на 3:

Ответ: скорость велосипедиста составляет 14 км/ч.

Разбор заданий тренировочного модуля

Чтобы сравнить данное выражение с нулём, нужно вспомнить, что значит число в третьей степени. Это значит, что число умножается само на себя три раза, В условии задачи – отрицательное число, при умножении знак «минус» будет повторяться три раза, значит, в результате получится отрицательное число, а любое отрицательное число меньше нуля.

Тип 2. Девочке задали на лето прочитать книгу, в которой х страниц. Она читала её три дня. В первый день девочка прочитала 21 страницу книги. Во второй день она прочитала 1/5 книги. В третий день она прочитала 1/2 от прочитанного во второй день. Сколько страниц она прочитала в третий день?