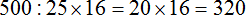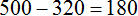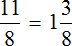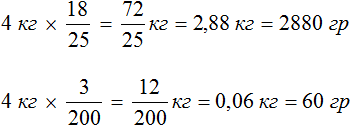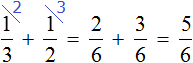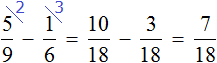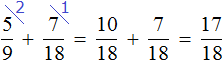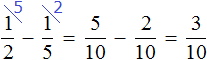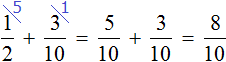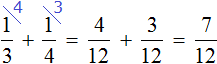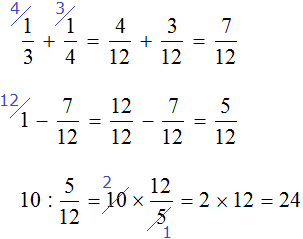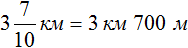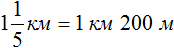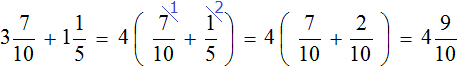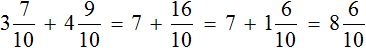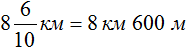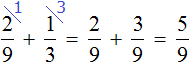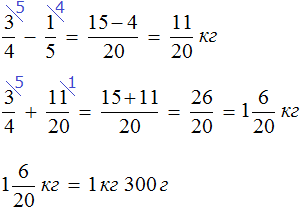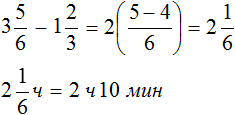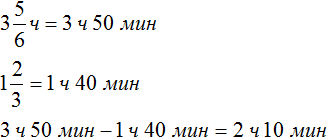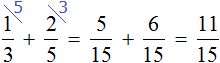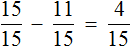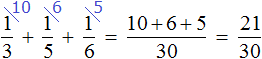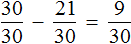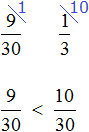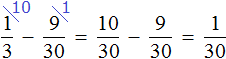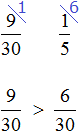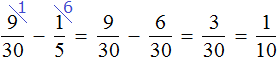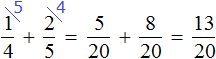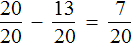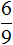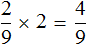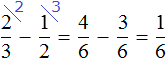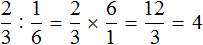Про уравнения - легко » Статьи

Как решать задачи уравнения с десятичными дробями

Обновлено
Решение уравнений с дробями

Как решать задачи уравнения с десятичными дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Содержание
  1. Понятие дроби
  2. Основные свойства дробей
  3. Понятие уравнения
  4. Понятие дробного уравнения
  5. Как решать уравнения с дробями
  6. 1. Метод пропорции
  7. 2. Метод избавления от дробей
  8. Что еще важно учитывать при решении
  9. Универсальный алгоритм решения
  10. Примеры решения дробных уравнений
  11. Задачи на дроби
  12. Задачи на дроби
  13. Задачи для самостоятельного решения
  14. 30 thoughts on “Задачи на дроби”
  15. Презентация по математике на тему «Действия с десятичными дробями. Решение задач с помощью уравнений.
  16. Описание презентации по отдельным слайдам:
  17. Краткое описание документа:
  18. Дистанционное обучение как современный формат преподавания
  19. Математика: теория и методика преподавания в образовательной организации
  20. Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
  21. Дистанционные курсы для педагогов
  22. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  23. Материал подходит для УМК
  24. Другие материалы
  25. Вам будут интересны эти курсы:
  26. Оставьте свой комментарий
  27. Автор материала
  28. Дистанционные курсы для педагогов
  29. Подарочные сертификаты
  30. 📹 Видео

Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Уравнения с десятичными дробями. Математика 5 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

  • обыкновенный вид — ½ или a/b,
  • десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

  1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
  2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 классСкачать

УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 класс

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Как решать уравнения с десятичными дробями - математика 5 класс

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

  • Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
  • Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит таках + b = 0, где a и b — действительные числа.

Что поможет в решении:

  • если а не равно нулю, то у уравнения единственный корень: х = −b : а;
  • если а равно нулю, а b не равно нулю — у уравнения нет корней;
  • если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Видео:Уравнение с десятичными дробямиСкачать

Уравнение с десятичными дробями

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Как решать задачи уравнения с десятичными дробями Как решать задачи уравнения с десятичными дробями

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

Как решать задачи уравнения с десятичными дробями Как решать задачи уравнения с десятичными дробями

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

Как решать задачи уравнения с десятичными дробями

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

Как решать задачи уравнения с десятичными дробями

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

Как решать задачи уравнения с десятичными дробями

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

Как решать задачи уравнения с десятичными дробями

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

  • подобрать число, которое можно разделить на каждый из знаменателей без остатка;
  • умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Как решать задачи уравнения с десятичными дробями

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

  • если значение переменной обращает знаменатель в 0, значит это неверное значение;
  • делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Уравнения с десятичными дробями в 5 классе (на умножение и деление).

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

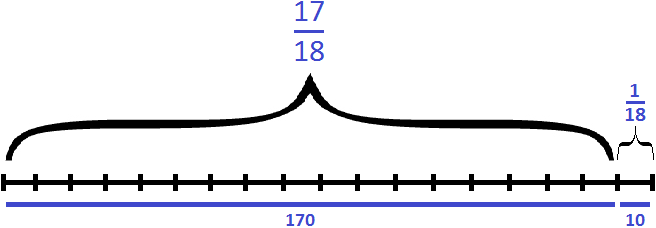
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

  1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
  2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
  3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравненияКак решать задачи уравнения с десятичными дробями

  1. Область допустимых значений: х ≠ −2.
  2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
  3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Как решать задачи уравнения с десятичными дробями

Переведем новый множитель в числитель..

Как решать задачи уравнения с десятичными дробями

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение: Как решать задачи уравнения с десятичными дробями

    Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

  • Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.

    • Видео:Уравнение на десятичные дроби со скобками и делением. Номер 391г.Скачать

    Уравнение на десятичные дроби со скобками и делением. Номер 391г.

    Задачи на дроби

    Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на дроби.

    Прежде чем решать задачи на дроби, необходимо досконально изучить все темы, касающиеся дробей. Ниже приведен список уроков, которые можно повторить.

    Каждая задача, приведенная в данном уроке, относится к категории элементарных. Если какая-то задача непонятна, это указывает на то, что предыдущий материал усвоен недостаточно хорошо.

    Видео:ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

    ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образование

    Задачи на дроби

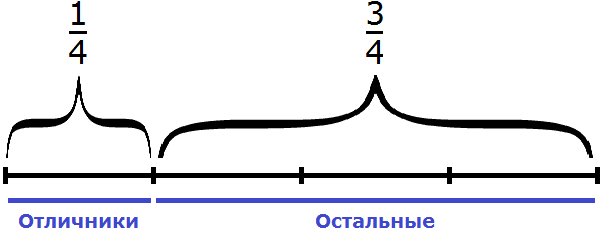
    Задача 1. В классе Как решать задачи уравнения с десятичными дробямишкольников составляют отличники. Какую часть составляют остальные? Сделать графическое описание задачи. Рисунок может быть любым.

    Решение

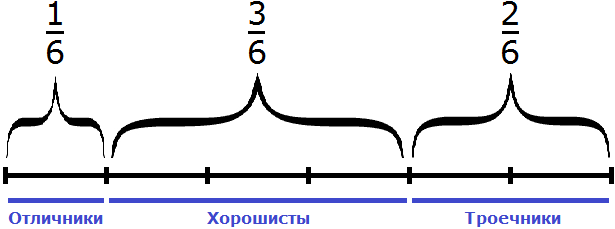
    Если Как решать задачи уравнения с десятичными дробямисоставляют отличники, то составляют остальные

    Как решать задачи уравнения с десятичными дробями

    Задача 2. В классе школьников составляют отличники, Как решать задачи уравнения с десятичными дробямисоставляют хорошисты, Как решать задачи уравнения с десятичными дробямисоставляют троечники. Сделать графическое описание задачи. Рисунок может быть любым.

    Как решать задачи уравнения с десятичными дробями

    Задача 3. В классе 24 школьника. школьников составляют отличники, Как решать задачи уравнения с десятичными дробямисоставляют хорошисты, Как решать задачи уравнения с десятичными дробямисоставляют троечники. Сколько в классе отличников, хорошистов и троечников?

    Решение

    24 : 6 × 1 = 4 × 1 = 4 (отличника)

    24 : 6 × 3 = 4 × 3 = 12 (хорошистов)

    24 : 6 × 2 = 4 × 2 = 8 (троечников)

    Проверка

    4 + 12 + 8 = 24 (школьника)

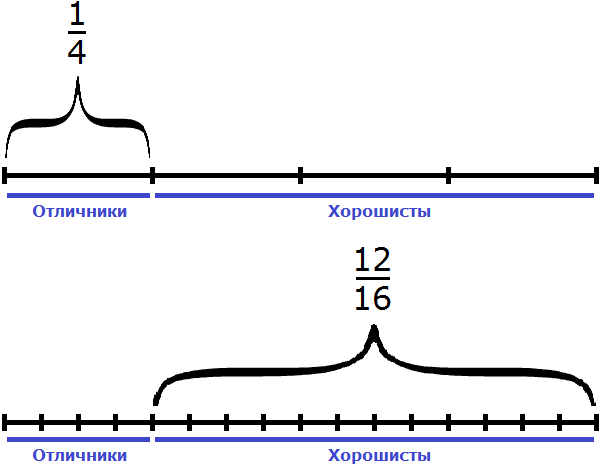
    Задача 4. В классе школьников составляют отличники, Как решать задачи уравнения с десятичными дробямисоставляют хорошисты. Какую часть составляют троечники?

    Решение

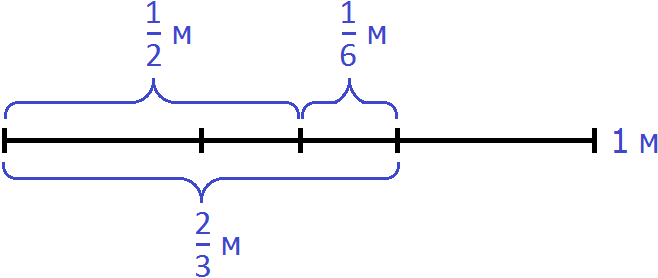
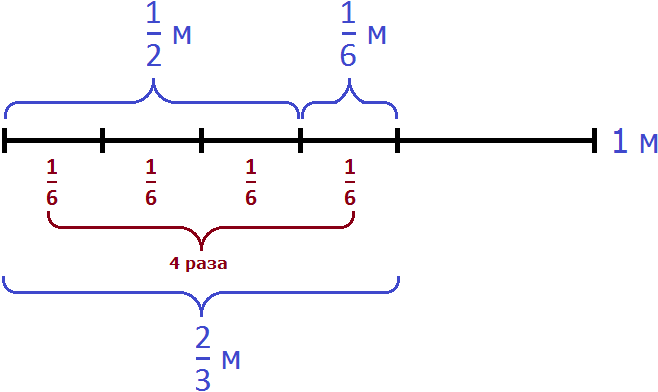
    Школьники разделены на 6 частей. На одну из частей приходятся отличники, на три части — хорошисты. Нетрудно догадаться, что на остальные две части приходятся троечники. Значит Как решать задачи уравнения с десятичными дробямишкольников составляют троечники

    Как решать задачи уравнения с десятичными дробями

    Не приводя рисунков можно сложить дроби и Как решать задачи уравнения с десятичными дробями, и полученный результат вычесть из дроби Как решать задачи уравнения с десятичными дробями, которая выражает всю часть школьников. Другими словами, сложить отличников и хорошистов, затем вычесть этих отличников и хорошистов из общего количества школьников

    Как решать задачи уравнения с десятичными дробями

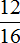
    Задача 5. В классе 16 школьников. Из них Как решать задачи уравнения с десятичными дробямисоставляют отличники, Как решать задачи уравнения с десятичными дробямисоставляют хорошисты. Сколько отличников и хорошистов в классе? Сделать графическое описание задачи. Рисунок может быть любым.

    Решение

    16 : 4 × 1 = 4 × 1 = 4 (отличника)

    16 : 16 × 12 = 1 × 12 = 12 (хорошистов)

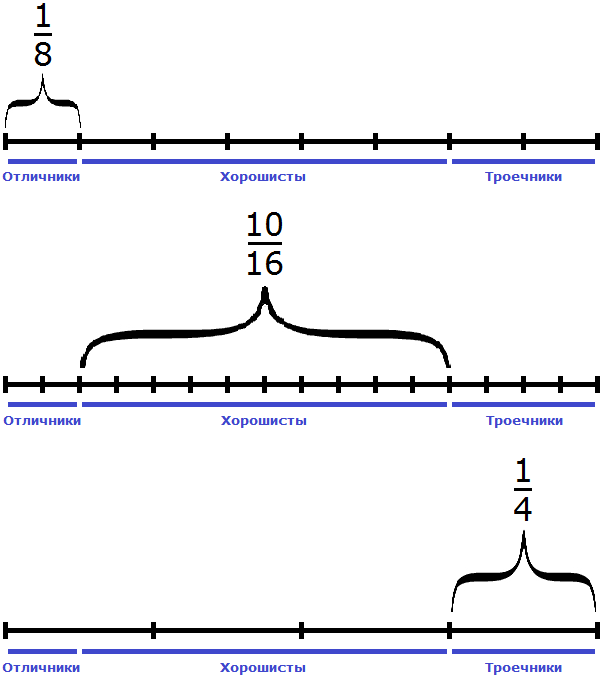
    Как решать задачи уравнения с десятичными дробями

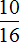
    Задача 6. В классе 16 школьников. Из них Как решать задачи уравнения с десятичными дробямисоставляют отличники, Как решать задачи уравнения с десятичными дробямисоставляют хорошисты, Как решать задачи уравнения с десятичными дробямисоставляют троечники. Сколько отличников, хорошистов и троечников в классе? Сделать графическое описание задачи. Рисунок может быть любым.

    Решение

    16 : 8 × 1 = 2 × 1 = 2 (отличника)

    16 : 16 × 10 = 1 × 10 = 10 (хорошистов)

    16 : 4 = 4 (троечника)

    Как решать задачи уравнения с десятичными дробями

    Задача 7. Из зерен пшеницы производят полтавскую крупу, масса которой составляет 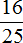Как решать задачи уравнения с десятичными дробямимассы зерна пшеницы, а остальное составляют кормовые отходы. Сколько можно получить полтавской крупы и кормовых отходов из 500 центнеров пшеницы

    Решение

    Найдем 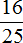Как решать задачи уравнения с десятичными дробямиот 500 центнеров:

    Как решать задачи уравнения с десятичными дробями

    Теперь найдем массу кормовых отходов. Для этого вычтем из 500 ц массу полтавской крупы:

    Как решать задачи уравнения с десятичными дробями

    Значит из 500 центнеров зерен пшеницы можно получить 320 центнеров полтавской крупы и 180 центнеров кормовых отходов.

    Задача 8. Килограмм сахара стоит 88 рублей. Сколько стоит Как решать задачи уравнения с десятичными дробямикг сахара? Как решать задачи уравнения с десятичными дробямикг? Как решать задачи уравнения с десятичными дробямикг? Как решать задачи уравнения с десятичными дробямикг?

    Решение

    1) Как решать задачи уравнения с десятичными дробямикг это половина одного килограмма. Если один килограмм стоит 88 рублей, то половина килограмма будет стоит половину от 88, то есть 44 рубля. Если найти половину от 88 рублей, мы получим 44 рубля

    44 × 1 = 44 рубля

    2) Как решать задачи уравнения с десятичными дробямикг это четверть килограмма. Если один килограмм стоит 88 рублей, то четверть килограмма будет стоит четверти от 88 рублей, то есть 22 рубля. Если найти Как решать задачи уравнения с десятичными дробямиот 88 рублей, мы получим 22 рубля

    22 × 1 = 22 рубля

    3) Дробь Как решать задачи уравнения с десятичными дробямиозначает, что килограмм разделен на восемь частей, и оттуда взято три части. Если один килограмм стоит 88 рублей, то стоимость трех восьми килограмм будут стоить Как решать задачи уравнения с десятичными дробямиот 88 рублей. Если найти Как решать задачи уравнения с десятичными дробямиот 88 рублей, мы получим 33 рубля.

    4) Дробь Как решать задачи уравнения с десятичными дробямиозначает, что килограмм разделен на восемь частей, и оттуда взято одиннадцать частей. Но невозможно взять одиннадцать частей, если их только восемь. Мы имеем дело с неправильной дробью. Сначала выделим в ней целую часть:

    Как решать задачи уравнения с десятичными дробями

    Одиннадцать восьмых это один целый килограмм и Как решать задачи уравнения с десятичными дробямикилограмма. Теперь мы можем по отдельности найти стоимость одного целого килограмма и стоимость трёх восьмых килограммов. Один килограмм, как было указано выше стоит 88 рублей. Стоимость Как решать задачи уравнения с десятичными дробямикг мы также находили и получили 33 рубля. Значит Как решать задачи уравнения с десятичными дробямикг сахара будет стоит 88+33 рубля, то есть 121 рубль.

    Стоимость Как решать задачи уравнения с десятичными дробямиможно найти не выделяя целой части. Для этого достаточно найти Как решать задачи уравнения с десятичными дробямиот 88.

    Но выделив целую часть можно хорошо понять, как сформировалась цена на Как решать задачи уравнения с десятичными дробямикг сахара.

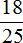
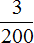
    Задача 9. Финики содержат Как решать задачи уравнения с десятичными дробямисахара и Как решать задачи уравнения с десятичными дробямиминеральных солей. Сколько граммов каждого из веществ содержится в 4 кг фиников?

    Решение

    Узнаем сколько граммов сахара содержится в одном килограмме фиников. Один килограмм это тысяча грамм. Найдем 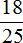Как решать задачи уравнения с десятичными дробямиот 1000 грамм:

    В одном килограмме фиников содержится 720 грамм сахара. Чтобы узнать сколько грамм сахара содержится в четырех килограммах, нужно 720 умножить на 4

    Теперь узнаем сколько минеральных солей содержится в 4 килограммах фиников. Но сначала узнаем сколько минеральных солей содержится в одном килограмме. Один килограмм это тысяча грамм. Найдем 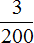Как решать задачи уравнения с десятичными дробямиот 1000 грамм:

    В одном килограмме фиников содержится 15 грамм минеральных солей. Чтобы узнать сколько грамм минеральных солей содержится в четырех килограммах, нужно 15 умножить на 4

    Значит в 4 кг фиников содержится 2880 грамм сахара и 60 грамм минеральных солей.

    Решение для данной задачи можно записать значительно короче, двумя выражениями:

    Как решать задачи уравнения с десятичными дробями

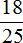
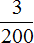
    Суть в том, что от 4 килограмм нашли Как решать задачи уравнения с десятичными дробямии полученные 2,88 перевели в граммы, умножив на 1000. Тоже самое сделали и для минеральных солей — от 4 кг нашли Как решать задачи уравнения с десятичными дробямии получившиеся килограммы перевели в граммы, умножив на 1000. Обратите также внимание на то, что дробь от числа найдена упрощенным способом — прямым умножением числа на дробь.

    Задача 10. Поезд прошел 840 км, что составляет Как решать задачи уравнения с десятичными дробямиего пути. Какое расстояние ему осталось пройти? Каково расстояние всего пути?

    Решение

    В задаче говорится, что 840 км это Как решать задачи уравнения с десятичными дробямиот его пути. Знаменатель дроби Как решать задачи уравнения с десятичными дробямиуказывает на то, что весь путь разделен на семь равных частей, а числитель указывает на то, что четыре части этого пути уже пройдено и составляют 840 км. Поэтому, разделив 840 км на 4, мы узнаем сколько километров приходится на одну часть:

    А поскольку весь путь состоит из семи частей, то расстояние всего пути можно найти, умножив 210 на 7:

    210 × 7 = 1470 км.

    Теперь ответим на второй вопрос задачи — какое расстояние осталось пройти поезду? Если длина пути 1470 км, а пройдено 840, то оставшийся путь равен 1470−840, то есть 630

    Задача 11. Одна из групп, покорившая горную вершину Эверест, состояла из спортсменов, проводников и носильщиков. Спортсменов в группе было 25, число проводников составляло Как решать задачи уравнения с десятичными дробямичисла спортсменов, а число спортсменов и проводников вместе лишь 9/140 числа носильщиков. Сколько было носильщиков в этой экспедиции?

    Решение

    Спортсменов группе 25. Проводников составляет Как решать задачи уравнения с десятичными дробямичисла спортсменов. Найдем Как решать задачи уравнения с десятичными дробямиот 25 и узнаем сколько в группе проводников:

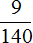
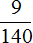
    Спортсменов и проводников вместе — 45 человек. Это число составляет Как решать задачи уравнения с десятичными дробямиот числа носильщиков. Зная что Как решать задачи уравнения с десятичными дробямиот числа носильщиков это 45 человек, мы можем найти общее число носильщиков. Для этого найдем число по дроби:

    45 : 9 × 140 = 5 × 140 = 700

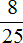
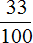
    Задача 12. В школу привезли 900 новых учебников, из них учебники по математике составляли Как решать задачи уравнения с десятичными дробямивсех книг, учебники по русскому языку Как решать задачи уравнения с десятичными дробямивсех книг, а остальные книги были по литературе. Сколько привезли книг по литературе

    Узнаем сколько составляют учебники по математике:

    900 : 25 × 8 = 288 (книг по математике)

    Узнаем сколько учебников по русскому языку:

    900 : 100 × 33 = 297 (книг по русскому языку)

    Узнаем сколько учебников по литературе. Для этого из общего числа книг вычтем учебники по математике и по русскому:

    900 – (288+297) = 900 – 585 = 315

    Проверка

    288 + 297 + 315 = 900

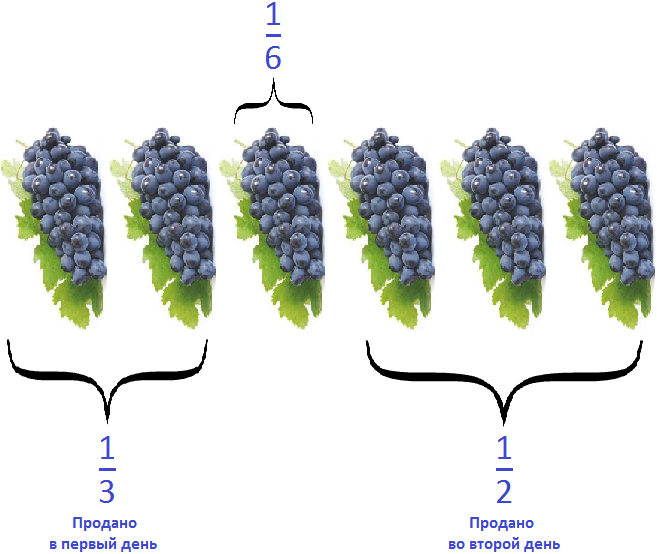
    Задача 13. В первый день продали Как решать задачи уравнения с десятичными дробями, а во второй день Как решать задачи уравнения с десятичными дробямипоступившего в магазин винограда. Какую часть винограда продали за два дня?

    Решение

    За два дня продали Как решать задачи уравнения с десятичными дробямивинограда. Эта часть получается путем сложения дробей Как решать задачи уравнения с десятичными дробямии Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Можно представить поступивший в магазин виноград в виде шести гроздей. Тогда Как решать задачи уравнения с десятичными дробямивинограда это две грозди, Как решать задачи уравнения с десятичными дробямивинограда — три грозди, а Как решать задачи уравнения с десятичными дробямивинограда это пять гроздей из шести, проданные за два дня. Ну и нетрудно увидеть, что осталась одна гроздь, выраженная дробь (одна гроздь из шести)

    Как решать задачи уравнения с десятичными дробями

    Задача 14. Вера в первый день прочитала Как решать задачи уравнения с десятичными дробямикниги, а во второй день на меньше. Какую часть книги прочитала Вера во второй день? Успела ли она прочитать книгу за два дня?

    Решение

    Определим часть книги, прочитанной во второй день. Сказано, что во второй день прочитано на меньше, чем в первый день. Поэтому из Как решать задачи уравнения с десятичными дробяминужно вычесть

    Как решать задачи уравнения с десятичными дробями

    Во второй день Вера прочитала 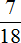Как решать задачи уравнения с десятичными дробямикниги. Теперь ответим на второй вопрос задачи — успела ли Вера прочитать книгу за два дня? Сложим то, что Вера прочитала в первый и во второй день:

    Как решать задачи уравнения с десятичными дробями

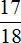
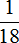
    За два дня Вера прочитала Как решать задачи уравнения с десятичными дробямикниги, но осталось ещё Как решать задачи уравнения с десятичными дробямикниги. Значит Вера не успела прочитать всю книгу за два дня.

    Сделаем проверку. Предположим что книга, которую читала Вера, имела 180 страниц. В первый день она прочла Как решать задачи уравнения с десятичными дробямикниги. Найдем Как решать задачи уравнения с десятичными дробямиот 180 страниц

    180 : 9 × 5 = 100 (страниц)

    Во второй день Вера прочитала на меньше, чем в первый. Найдем от 180 страниц, и вычтем полученный результат из 100 листов, прочитанных в первый день

    180 : 6 × 1 = 30 × 1 = 30 (страниц)

    100 − 30 = 70 (страниц во второй день)

    Проверим, являются ли 70 страниц 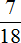Как решать задачи уравнения с десятичными дробямичастью книги:

    180 : 18 × 7 = 10 × 7 = 70 (страниц)

    Теперь ответим на второй вопрос задачи — успела ли Вера прочитать все 180 страниц за два дня. Ответ — не успела, поскольку за два дня она прочла только 170 страниц

    100 + 70 = 170 (страниц)

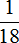
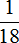
    Осталось прочесть еще 10 страниц. В задаче в роли остатка у нас была дробь Как решать задачи уравнения с десятичными дробями. Проверим являются ли 10 страниц Как решать задачи уравнения с десятичными дробямичастью книги?

    180 : 18 × 1 = 10 × 1 = 10 (страниц)

    Как решать задачи уравнения с десятичными дробями

    Задача 15. В одном пакете Как решать задачи уравнения с десятичными дробямикг, а в другом на Как решать задачи уравнения с десятичными дробямикг меньше. Сколько килограммов конфет в двух пакетах вместе?

    Решение

    Определим массу второго пакета. Она на Как решать задачи уравнения с десятичными дробямикг меньше, чем масса первого пакета. Поэтому из массы первого пакета вычтем массу второго:

    Как решать задачи уравнения с десятичными дробями

    Масса второго пакета 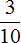Как решать задачи уравнения с десятичными дробямикг. Определим массу обоих пакетов. Сложим массу первого и массу второго:

    Как решать задачи уравнения с десятичными дробями

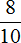
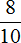
    Масса обоих пакетов Как решать задачи уравнения с десятичными дробямикг. А Как решать задачи уравнения с десятичными дробямикилограмма это 800 граммов. Можно решать такую задачу, работая с дробями, складывая и вычитая их. Также можно сначала найти число по данным в задаче дробям и приступить к решению. Так Как решать задачи уравнения с десятичными дробямикилограмма это 500 граммов, а Как решать задачи уравнения с десятичными дробямикг это 200 граммов

    1000 : 2 × 1 = 500 × 1 = 500 г

    1000 : 5 × 1 = 200 × 1 = 200 г

    Во втором пакете на 200 граммов меньше, поэтому чтобы определить массу второго пакета, нужно из 500 г вычесть 200 г

    500 − 200 = 300 г

    Ну и напоследок сложить массы обоих пакетов:

    500 + 300 = 800 г

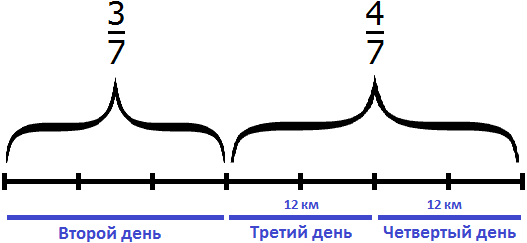
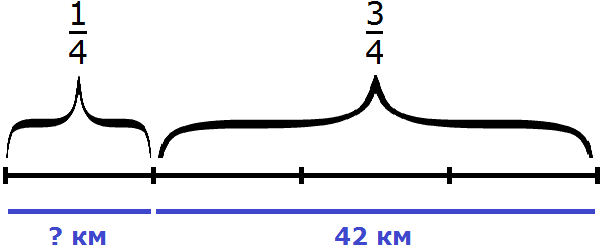
    Задача 16. Туристы прошли путь от турбазы до озера за 4 дня. В первый день они прошли Как решать задачи уравнения с десятичными дробямивсего пути, во второй Как решать задачи уравнения с десятичными дробямиоставшегося пути, а в третий и четвертый дни проходили по 12 км. Чему равна длина всего пути от турбазы до озера?

    Решение

    В задаче сказано, что во второй день туристы прошли Как решать задачи уравнения с десятичными дробямиоставшегося пути . Дробь Как решать задачи уравнения с десятичными дробямиозначает, что оставшийся путь разделен на 7 равных частей, из них туристы прошли три части, но осталось пройти остальные Как решать задачи уравнения с десятичными дробями. На эти Как решать задачи уравнения с десятичными дробямиприходится то расстояние, которое туристы прошли в третий и четвертый день, то есть 24 км (по 12 км в каждом дне). Нарисуем наглядную схему, иллюстрирующую второй, третий и четвертый дни:

    Как решать задачи уравнения с десятичными дробями

    В третий и четвертый день туристы прошли 24 км и это составляет Как решать задачи уравнения с десятичными дробямиот пути, пройденного во второй, третий и четвертый дни. Зная, что Как решать задачи уравнения с десятичными дробямисоставляют 24 км, мы можем найти весь путь, пройденный во второй, третий и четвертый день:

    24 : 4 × 7 = 6 × 7 = 42 км

    Во второй, третий и четвертый день туристы прошли 42 км. Теперь найдем Как решать задачи уравнения с десятичными дробямиот этого пути. Так мы узнаем сколько километров туристы прошли во второй день:

    42 : 7 × 3 = 6 × 3 = 18 км

    Теперь возвращаемся к началу задачи. Сказано, что в первый день туристы прошли Как решать задачи уравнения с десятичными дробямивсего пути. Весь путь разделен на четыре части, и на первую часть приходится путь, пройденный в первый день. А путь, который приходится на остальные три части, мы уже нашли — это 42 километра, пройденные во второй, третий и четвертый дни. Нарисуем наглядную схему, иллюстрирующую первый и остальные три дня:

    Как решать задачи уравнения с десятичными дробями

    Зная, что пути составляют 42 километра, мы можем найти длину всего пути:

    42 : 3 × 4 = 56 км

    Значит длина пути от турбазы до озера составляет 56 километров. Сделаем проверку. Для этого сложим все пути, пройденные туристами в каждый из четырех дней.

    Сначала найдем путь пройденный в первый день:

    56 : 4 × 1 = 14 (в первый день)

    14 + 18 + 12 + 12 = 56

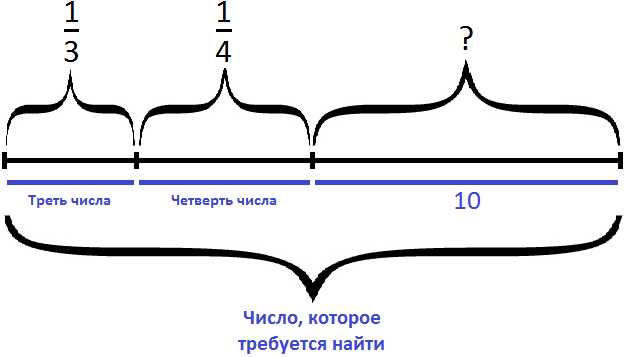
    Задача из арифметики известного среднеазиатского математика Мухаммеда ибн-Мусы ал-Хорезми (IX век н. э.)

    «Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10»

    Изобразим число, которое мы хотим найти, в виде отрезка, разделенного на три части. В первой части отрезка отметим треть, во второй — четверть, оставшаяся третья часть будет изображать число 10.

    Как решать задачи уравнения с десятичными дробями

    Сложим треть и четверть:

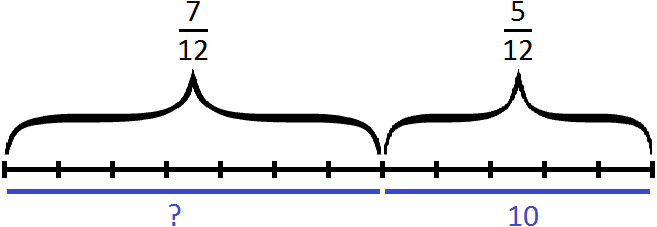
    Как решать задачи уравнения с десятичными дробями

    Теперь изобразим отрезок, разделенный на 12 частей. Отметим на нем дробь 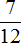Как решать задачи уравнения с десятичными дробями, остальные пять частей пойдут на число 10:

    Как решать задачи уравнения с десятичными дробями

    Зная, что пять двенадцатых числа составляют число 10, мы можем найти всё число:

    10 : 5 × 12 = 2 × 12 = 24

    Мы нашли всё число — оно равно 24.

    Эту задачу можно решить не приводя рисунков. Для этого, сначала нужно сложить треть и четверть. Затем из единицы, которая играет роль неизвестного числа, вычесть результат сложения трети и четверти. Затем по полученной дроби определить всё число:

    Как решать задачи уравнения с десятичными дробями

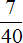
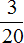
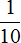
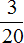
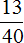
    Задача 17. Семья, состоящая из четырех человек, в месяц зарабатывает 80 тысяч рублей. Бюджет распланирован следующим образом: Как решать задачи уравнения с десятичными дробямина еду, Как решать задачи уравнения с десятичными дробямина коммунальные услуги, Как решать задачи уравнения с десятичными дробямина Интернет и ТВ, Как решать задачи уравнения с десятичными дробямина лечение и походы по врачам, Как решать задачи уравнения с десятичными дробямина пожертвование в детский дом, Как решать задачи уравнения с десятичными дробямина проживание в съемной квартире, Как решать задачи уравнения с десятичными дробямив копилку. Сколько денег выделено на еду, коммунальные услуги, на Интернет и ТВ, на лечение и походы по врачам, пожертвование на детский дом, на проживание в съемной квартире, и на копилку?

    Решение

    80 : 40 × 7 = 14 (тыс. на еду)

    80 : 20 × 1 = 4 × 1 = 4 тыс. (на коммунальные услуги)

    80 : 20 × 1 = 4 × 1 = 4 тыс. (на Интернет и ТВ)

    80 : 20 × 3 = 4 × 3 = 12 тыс. (на лечение и походы по врачам)

    80 : 10 × 1 = 8 × 1 = 8 тыс. (на пожертвование в детский дом)

    80 : 20 × 3 = 4 × 3 = 12 тыс. (на проживание в съемной квартире)

    80 : 40 × 13 = 2 × 13 = 26 тыс. (в копилку)

    Проверка

    14 + 4 + 4 + 12 + 8 + 12 + 26 = 80

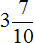
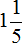
    Задача 18. Туристы во время похода за первый час прошли Как решать задачи уравнения с десятичными дробямикм, а за второй на Как решать задачи уравнения с десятичными дробямикм больше. Сколько километров прошли туристы за два часа?

    Решение

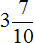
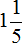
    Найдем числа по дробям. Как решать задачи уравнения с десятичными дробямиэто три целых километра и семь десятых километра, а семь десятых километра это 700 метров:

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробямиэто один целый километр и одна пятая километра, а одна пятая километра это 200 метров

    Как решать задачи уравнения с десятичными дробями

    Определим длину пути, пройденного туристами за второй час. Для этого к 3 км 700 м нужно прибавить 1 км 200 м

    3 км 700 м + 1 км 200 м = 3700м + 1200м = 4900м = 4 км 900 м

    Определим длину пути, пройденного туристами за два часа:

    3 км 700 м + 4 км 900 = 3700м + 4900м = 8600м = 8 км 600 м

    Значит за два часа туристы прошли 8 километров и еще 600 метров. Решим эту задачу с помощью дробей. Так её можно значительно укоротить

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

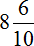
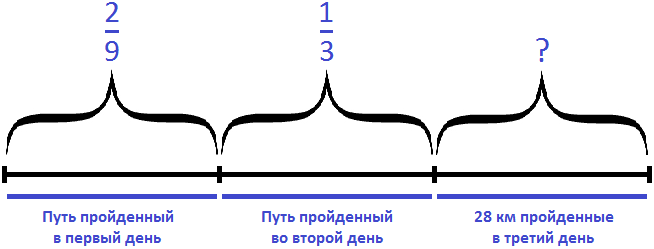
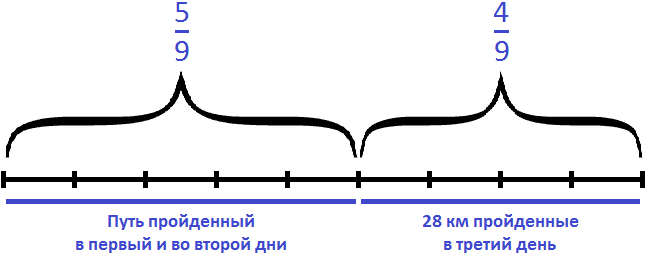
    Получили ответ Как решать задачи уравнения с десятичными дробямикилометра. Это восемь целых километров и шесть десятых километра, а шесть десятых километра это шестьсот метров

    Как решать задачи уравнения с десятичными дробями

    Задача 19. Геологи прошли долину, расположенную между горами, за три дня. В первый день они прошли Как решать задачи уравнения с десятичными дробями, во второй Как решать задачи уравнения с десятичными дробямивсего пути и в третий оставшиеся 28 км. Вычислить длину пути, проходящего по долине.

    Решение

    Изобразим путь в виде отрезка, разделенного на три части. В первой части отметим Как решать задачи уравнения с десятичными дробямипути, во второй части Как решать задачи уравнения с десятичными дробямипути, в третьей части оставшиеся 28 километров:

    Как решать задачи уравнения с десятичными дробями

    Сложим части пути, пройденные в первый и во второй день:

    Как решать задачи уравнения с десятичными дробями

    За первый и второй дни геологи прошли Как решать задачи уравнения с десятичными дробямивсего пути. На остальные Как решать задачи уравнения с десятичными дробямипути приходятся 28 километров, пройденные геологами в третий день. Зная, что 28 километров это Как решать задачи уравнения с десятичными дробямивсего пути, мы можем найти длину пути, проходящего по долине:

    28 : 4 × 9 = 7 × 9 = 63 км

    Как решать задачи уравнения с десятичными дробями

    Проверка

    63 : 9 × 5 = 7 × 5 = 35

    63 : 9 × 4 = 7 × 4 = 28

    Задача 20. Для приготовления крема использовали сливки, сметану и сахарную пудру. Сметану и сливки составляют 844,76 кг, а сахарная пудра и сливки 739,1 кг. Сколько в отдельности сливок, сметаны и сахарной пудры содержится в 1020,85 кг крема?

    Решение

    сметана и сливки — 844,76 кг
    сахарная пудра и сливки — 739,1 кг

    Вытащим из 1020,85 кг крема сметану и сливки (844,76 кг). Так мы найдем массу сахарной пудры:

    1020,85 кг — 844,76 кг = 176,09 (кг сахарной пудры)

    Вытащим из сахарной пудры и сливок сахарную пудру (176,09 кг). Так мы найдем массу сливок:

    739,1 кг — 176,09 кг = 563,01 (кг сливок)

    Вытащим сливки из сметаны и сливок. Так мы найдем массу сметаны:

    844,76 кг — 563,01 кг = 281,75 (кг сметаны)

    176,09 (кг сахарная пудра)

    563,01 (кг сливки)

    281,75 (кг сметана)

    Проверка

    176,09 кг + 563,01 кг + 281,75 кг = 1020,85 кг

    1020,85 кг = 1020,85 кг

    Задача 21. Масса бидона, заполненного молоком равна 34 кг. Масса бидона, заполненного наполовину, равна 17,75 кг. Какова масса пустого бидона?

    Решение

    Вычтем из массы бидона, заполненного молоком, массу бидона заполненного наполовину. Так мы получим массу содержимого бидона, заполненного наполовину, но уже без учета массы бидона:

    34 кг − 17,75 кг = 16,25 кг

    16,25 это масса содержимого бидона заполненного наполовину. Умножим эту массу на 2, получим массу бидона заполненного полностью:

    16,25 кг × 2 = 32,5 кг

    32,5 кг это масса содержимого бидона. Чтобы вычислить массу пустого бидона, нужно из 34 кг вычесть массу его содержимого, то есть 32,5 кг

    34 кг − 32,5 кг = 1,5 кг

    Ответ: масса пустого бидона составляет 1,5 кг.

    Задача 22. Сливки составляют 0,1 массы молока, а сливочное масло составляет 0,3 массы сливок. Сколько сливочного масла можно получить из суточного надоя коровы, равного 15 кг молока?

    Решение

    Определим сколько килограмм сливок можно получить с 15 кг молока. Для этого найдем 0,1 часть от 15 кг.

    15 × 0,1 = 1,5 (кг сливок)

    Теперь определим сколько сливочного масла можно получить с 1,5 кг сливок. Для этого найдем 0,3 часть от 1,5 кг

    1,5 кг × 0,3 = 0,45 (кг сливочного масла)

    Ответ: из 15 кг молока можно получить 0,45 кг сливочного масла.

    Задача 23. 100 кг клея для линолеума содержат 55 кг асфальта, 15 кг канифоли, 5 кг олифы и 25 кг бензина. Какую часть этого клея образует каждая из его составляющих?

    Решение

    Представим, что 100 кг клея как 100 частей. Тогда на 55 частей приходится асфальт, на 15 частей — канифоль, на 5 частей — олифа, на 25 частей — бензин. Запишем эти части в виде дробей, и по возможности сократим получающиеся дроби:

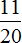
    Как решать задачи уравнения с десятичными дробями

    Ответ: Как решать задачи уравнения с десятичными дробямиклея составляет асфальт, Как решать задачи уравнения с десятичными дробямисоставляет канифоль, Как решать задачи уравнения с десятичными дробямисоставляет олифа, Как решать задачи уравнения с десятичными дробямисоставляет бензин.

    Видео:Решение уравнений, 6 классСкачать

    Решение уравнений, 6 класс

    Задачи для самостоятельного решения

    Решение

    Как решать задачи уравнения с десятичными дробями

    Ответ: масса двух пакетов вместе составляет 1 кг 300 г

    Решение

    Как решать задачи уравнения с десятичными дробями

    Второй способ

    Как решать задачи уравнения с десятичными дробями

    Ответ: театральное представление длилось 2 часа 10 минут.

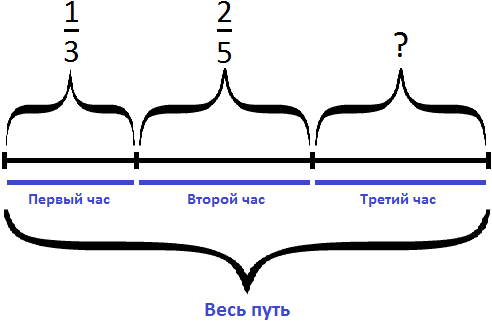
    Решение

    Как решать задачи уравнения с десятичными дробями

    Определим часть пути, пройденного лыжником за два часа движения. Для этого сложим дроби, выражающие пути пройденные за первый и второй час:

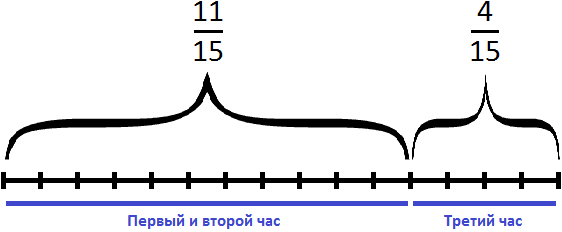
    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Определим часть пути, пройденного лыжником за третий час. Для этого из всех частей вычтем часть пути, пройденного за первый и второй час движения:

    Как решать задачи уравнения с десятичными дробями

    Ответ: в третий час лыжник прошел Как решать задачи уравнения с десятичными дробямивсего расстояния.

    Решение

    Определим часть школьников, которые участвовали в футболе, баскетболе и в прыжках:

    Как решать задачи уравнения с десятичными дробями

    Определим часть школьников, которые участвовали в беге:

    Как решать задачи уравнения с десятичными дробями

    Узнаем на какую часть бегунов больше (или меньше) чем футболистов. Для начала сравним дроби 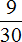Как решать задачи уравнения с десятичными дробямии Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Требовалось узнать на какую часть бегунов больше (или меньше) чем футболистов. Мы выяснили, что бегунов меньше, чем футболистов. Выясним на какую часть их меньше:

    Как решать задачи уравнения с десятичными дробями

    Бегунов меньше, чем футболистов на Как решать задачи уравнения с десятичными дробямичасть.

    Теперь узнаем на какую часть бегунов больше (или меньше) чем баскетболистов. Для начала сравним дроби 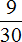Как решать задачи уравнения с десятичными дробямии Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Требовалось узнать на какую часть бегунов больше (или меньше) чем баскетболистов. Мы выяснили, что бегунов больше, чем баскетболистов. Выясним на какую часть их больше:

    Как решать задачи уравнения с десятичными дробями

    Бегунов больше, чем баскетболистов на часть.

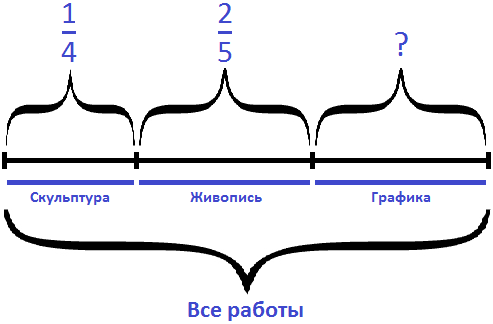
    Ответ: бегунов было на Как решать задачи уравнения с десятичными дробямичасть меньше, чем футболистов и на часть больше, чем баскетболистов.

    Задача 5. На выставке художественных работ представлена живопись, скульптура и графика. Как решать задачи уравнения с десятичными дробямивсех работ составляет скульптура, Как решать задачи уравнения с десятичными дробями– живопись, оставшуюся часть – графика. Какую часть всех работ составляет графика?

    Решение

    Как решать задачи уравнения с десятичными дробями

    Сложим дроби, выражающие скульптуру и живопись:

    Как решать задачи уравнения с десятичными дробями

    Определим какую часть всех работ составляет графика:

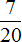
    Как решать задачи уравнения с десятичными дробями

    Ответ: Как решать задачи уравнения с десятичными дробямивсех работ составляет графика.

    Задача 6. Рабочие отремонтировали дорогу длиной 820 м за три дня. Во вторник они отремонтировали Как решать задачи уравнения с десятичными дробямиэтой дороги, а в среду оставшейся части. Сколько метров дороги отремонтировали рабочие в четверг?

    Решение

    Определим длину дороги, отремонтированной во вторник:

    820 : 5 × 2 = 328 м

    Определим длину дороги, отремонтированной в среду. Известно, что в этот день рабочие отремонтировали оставшейся дороги. Оставшаяся дорога это 820−328, то есть 492

    492 : 3 × 2 = 328 м

    Определим длину дороги, отремонтированной в четверг. Для этого вычтем из 820 длины дорог, отремонтированных во вторник и в среду:

    820 − (328 + 328) = 820 − 656 = 164 м

    Ответ: в четверг рабочие отремонтировали 164 метра дороги.

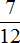
    Задача 7. В книге три рассказа. Наташа прочла первый рассказ за Как решать задачи уравнения с десятичными дробямич, на чтение второго рассказа она потратила на ч больше, а чтение третьего рассказа заняло на Как решать задачи уравнения с десятичными дробямич меньше, чем чтение первого и второго рассказов вместе. Сколько времени ушло у Наташи на чтение всей книги?

    Решение

    Определим время за которое Наташа прочитала первый рассказ. Она прочила его за треть часа. Треть часа это 20 минут

    60 : 3 × 1 = 20 минут

    Определим время за которое Наташа прочитала второй рассказ. Она прочила его на ч больше. часа это 10 минут. Прибавим к 20 минутам 10 минут, получим время чтения второго рассказа:

    20 + 10 = 30 минут

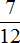
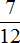
    Определим время за которое Наташа прочитала третий рассказ. Она прочитала его на Как решать задачи уравнения с десятичными дробямич меньше, чем чтение первого и второго рассказов вместе. Как решать задачи уравнения с десятичными дробямичаса это 35 минут. Вычтем 35 из времени, затраченного на чтение первого и второго рассказа вместе (50 м)

    Определим сколько времени ушло у Наташи на чтение всей книги:

    20 + 30 + 15 = 65 минут = 1 ч 5 минут

    На чтение всей книги у Наташи ушел 1 час и 5 минут. Решим эту задачу с помощью дробей. Так ее можно значительно укоротить:

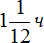
    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробямиэто один целый час и Как решать задачи уравнения с десятичными дробямичаса, а одну двенадцатую часа составляют 5 минут.

    Ответ: на чтение всей книги у Наташи ушло Как решать задачи уравнения с десятичными дробями

    Задача 8. Из одной тонны хлопка-сырца можно изготовить 3400 м ткани, 1,05 ц пищевого масла и 0,225 т жмыха. Сколько метров ткани, пищевого масла и жмыха можно получить из 32,4 ц хлопка-сырца?

    Решение

    Переведем 32,4 ц в тонны. Одна тонна составляет 10 центнеров. Чтобы узнать сколько таких десять центнеров (имеется ввиду тонн) в 32,4 центнерах, нужно 32,4 разделить на 10

    Определим сколько метров ткани можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 3400 метров ткани. А с 3,24 тонн будет получено в 3,24 раза больше ткани

    3400 × 3,24 = 11016 метров ткани.

    Определим сколько пищевого масла можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 1,05 ц пищевого масла. А с 3,24 тонн будет получено в 3,24 раза больше масла

    1,05 × 3,24 = 3,402 центнера пищевого масла

    Определим сколько жмыха можно получить с 3,24 тонн хлопка-сырца. С одной тонны, как указано в задаче, получается 0,225 т жмыха. А с 3,24 тонн будет получено в 3,24 раза больше жмыха

    0,225 × 3,24 = 0,729 тонн жмыха

    Ответ: из 32,4 ц хлопка сырца можно получить 11016 метров ткани, 3,402 ц пищевого масла и 0,729 т жмыха.

    Решение

    Зная, что 0,2 всего пути составляют 12 км, мы можем найти весь путь. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь

    Ответ: Туристы прошли 60 км.

    Решение

    Зная, что 0,7 книги составляют 56 страниц, мы можем узнать сколько всего страниц в книге. Чтобы найти неизвестное число по десятичной дроби, нужно известное число разделить на десятичную дробь

    56 : 0,7 = 80 (страниц всего)

    Узнаем сколько осталось прочитать

    80 − 56 = 24 (страницы осталось прочитать)

    Ответ: в книге 80 страниц. Прочитать осталось еще 24 страницы.

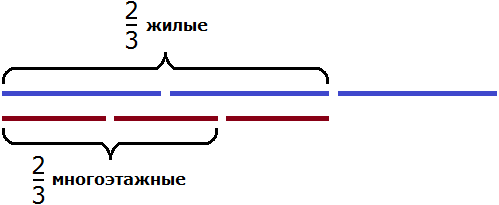
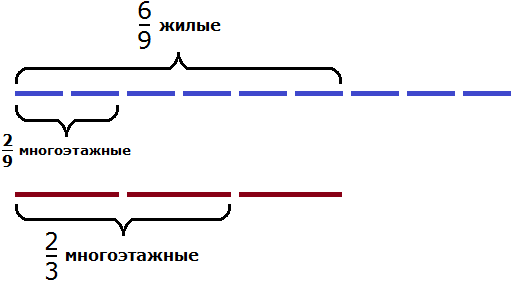
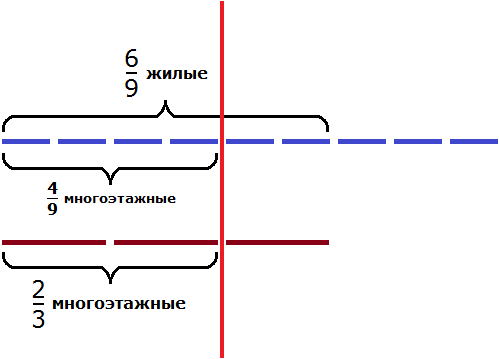
    Решение

    Как решать задачи уравнения с десятичными дробями

    Разделим жилых домов на три части:

    Как решать задачи уравнения с десятичными дробями

    Теперь на треть многоэтажных домов приходится 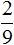Как решать задачи уравнения с десятичными дробямивсех зданий. Изначально все здания были разделены на три равные части. Теперь они разделены на девять равных частей. Жилые дома, которые ранее выражались дробью , теперь выражаются дробью Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Чтобы узнать сколько многоэтажных домов приходится на две трети, умножим 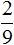Как решать задачи уравнения с десятичными дробямина 2

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

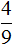
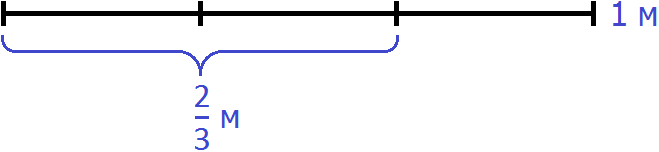
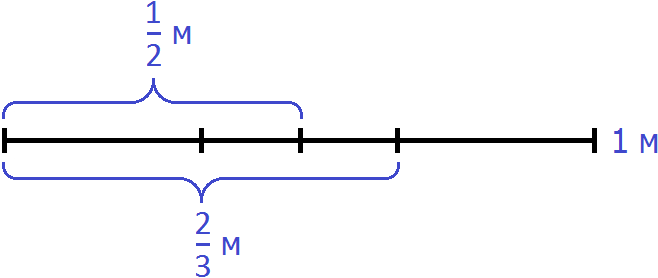
    Ответ: жилые многоэтажные дома составляют Как решать задачи уравнения с десятичными дробямивсех зданий в городе.

    Решение

    Изобразим схематически один метр веревки:

    Как решать задачи уравнения с десятичными дробями

    Выделим на этом рисунке метра:

    Как решать задачи уравнения с десятичными дробями

    Здесь же выделим Как решать задачи уравнения с десятичными дробямиметра

    Как решать задачи уравнения с десятичными дробями

    Не выделенным на м остался один кусочек. Узнаем, что это за кусочек. Для этого из вычтем Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    м это часть веревки, которую нужно отрезать. Тогда мы получим Как решать задачи уравнения с десятичными дробямим веревки.

    Теперь осталось узнать сколько раз м содержит м

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Значит, чтобы не производя измерений от м веревки отрезать Как решать задачи уравнения с десятичными дробямим, нужно эту веревку сложить вчетверо и отрезать одну часть. Оставшаяся часть и будет половиной от одного метра.

    Ответ: чтобы от веревки, длина которой м отрезать Как решать задачи уравнения с десятичными дробямим, нужно сложить эту веревку вчетверо и отрезать от неё одну часть. Оставшаяся часть станет Как решать задачи уравнения с десятичными дробямим веревки.

    Понравился урок?
    Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

    Возникло желание поддержать проект?
    Используй кнопку ниже

    Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

    Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.

    30 thoughts on “Задачи на дроби”

    Здравствуйте! Очень благодарна вам за ваши труды. Очень все доступно объясняете.
    В задаче №2 есть опечатка. В условии одна целая пять шестых часа, а в решении одна целая две трети.

    Добавлю, что задача №2 в разделе самостоятельного решения.

    Здравствуйте! Спасибо вам большое за задачи!
    Но я никак не могу понять, почему в 16 задаче такое решение. Почему 3/7 оставшегося пути не вычисляются из 24км? Ведь второй день = 3/7 оставшегося пути, этот путь равен 24км. Он не может включать и второй день? Разве нет?

    24 км это путь, пройденный в третий и четвертый дни. А во второй день было пройдено совсем другое расстояние.

    Вообще, во второй, третий и четвертый дни всего было пройдено 42 км.

    Найдите от 42 км сначала 3/7 пути, а потом 4/7 пути. Сразу станет всё понятно 😉

    А откуда в 3-й задаче взялась дробь 15 на 15?

    Видео:Уравнение. 5 класс.Скачать

    Уравнение. 5 класс.

    Презентация по математике на тему «Действия с десятичными дробями. Решение задач с помощью уравнений.

    Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

    Как решать задачи уравнения с десятичными дробями

    Описание презентации по отдельным слайдам:

    Как решать задачи уравнения с десятичными дробями

    Тема урока Закрепление по теме: «Действия с десятичными дробями. Решение задач с помощью уравнений»

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    РЕШИТЕ 1) х + 5,9= 8,7 М 7) х + 3,7 = 6,8 Х 2) 7,45 – х = 4,3 К 8) 8,26 — х = 4,2 И 3) х : 3 = 5,2 О 9) х : 2 = 7,4 Ш 4) 9,03 * к= 90,3 Т 10) 8,3 * к = 830 Л 5) 9,5 + а = 16,8 У 11) 10,9 + а = 6,3 О 6) 2,3 * 11 = В 12) 2,3 * 11 = В

    Как решать задачи уравнения с десятичными дробями

    ЗАПОЛНИТЕ ТАБЛИЦУ 3,1 15,6 10 4,06 3,2 14,8 3,15 4,6 100 7,3 25,3

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    Решение задач с помощью уравнений.

    Как решать задачи уравнения с десятичными дробями

    ЗАДАЧА №1 В швейной мастерской было 60,86 м цветной ленты. Красной ленты было меньше, чем синей на 7,26 м. Зелёной в 2 раза больше, чем синей. Сколько метров синей ленты всего было в мастерской? С. – ? К. — ?, на 7,26м меньше, чем С. 60,86м З. — ?, в 2 раза больше, чем С.

    Как решать задачи уравнения с десятичными дробями

    РЕШЕНИЕ х + х – 7,26 + 2х = 60,86 4х = 60,86 + 7,26 4Х = 68,12 Х= 68,12 : 4 Х= 17,03 17,03 + 17,03 – 7,26 + 2 · 17,03 = 60,86 Ответ: 17,03 м синей ленты .

    Как решать задачи уравнения с десятичными дробями

    Как решать задачи уравнения с десятичными дробями

    ЗАДАЧА №2 В двух корзинах 2,24 кг яблок. В одной корзине в 3 раза больше яблок, чем в другой. Сколько килограммов яблок в каждой корзине?

    Как решать задачи уравнения с десятичными дробями

    Спасибо, ребята, за активную работу.

    Краткое описание документа:

    Дети, приступившие к обучению, поднимают ладошку . Каждому ребёнку даётся по 2-3 секунды для приветствия.

    Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

    Задачи: Организовать самоопределение детей к деятельности на уроке. эмоциональный настрой.

    Ребята, вы отлично поработали с заданиями на сайте Учи.ру. Команда сайта отметила вашу активность грамотами. Надеюсь, что сегодня мы с таким же боевым настроем будем систематизировать полученные знания.

    Объявляет тему урока.

    Мы сегодня будем работать командами. Команда девочек , команда мальчиков

    Каждый ученик, правильно ответивший на вопрос будет в чате получать цветок своей команды. В конце урока мы посмотрим, у какой команды букет получился более пышным.

    Кто готов к уроку, поднимите

    в знакомой ситуации (типовые)

    Спрашивает, как можно объяснить правила вычисления десятичных дробей.

    Спрашивает, кому из учащихся нужно ещё раз повторить данные темы. Если возникают вопросы, повторяет на примере данную тему.

    Предполагаемый правильный ответ:

    Если записать десятичные дроби «в столбик» так, что запятая окажется под запятой, то будет выполняться поразрядное сложение чисел. Что для наглядности можно написать незначащие нули после запятой в одном из чисел, чтобы уровнять в числа количество знаков после запятой. Главное, чтобы при записи в столбик запятая оказалась под запятой.

    Предполагаемый правильный ответ:

    Если при умножении на 10,100,1000 запятая переносится вправо на столько цифр, сколько нулей.

    При делении влево….

    Предполагаемый правильный ответ:

    Напоминает, что при умножении в столбик запись чисел производится, не обращая внимания на запятые. После вычисления, влево отсчитывается столько цифр, сколько цифр всего после запятой.

    Предлагает учащимся выполнить задание, чтобы систематизировать знания по темам «Действия с десятичными дробями» и «Решение уравнений».

    Команда Ромашка выполняет задания первого столбика, команда Колокольчик, задания второго столбика.

    Выполняют задание учителя.

    Когда закончили работу, поднимают ладошку.

    Отвечают те, кому учитель даёт слово.

    Изучает результаты выполнения теста учащимися, при необходимости даѐт дополнительные комментарии к выполненным заданиям.

    Вопрос 1

    Поочерёдно даёт слово учащимся, поднявшим

    Если ученик даёт неправильный ответ, предлагает вспомнить и объяснить правило умножения, сложения, или вычитания дробей.

    Вопрос 2

    Спрашивает, кто из учащихся согласен с этим предложением.

    Вопрос 3

    Спрашивает, что интересного заметили в предложенных заданиях.

    Вопрос 4

    Просит объяснить, ссылаясь на определения – «уравнения», «числовые выражения»

    Вопрос 5

    Спрашивает каким способом пользовались,умножая на 11.

    Изучают результаты проверки теста и комментарии к выполненным заданиям. Разбираются с допущенными ошибками.

    Все, кроме 12 и 6 заданий, уравнения

    Предполагаемый правильный ответ:

    Уравнение — это равенство, содержащее букву, значение которой надо найти.

    Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок.

    Одному ученику предоставляется возможность написать на доске и объяснить способ умножения на 11.

    Зарядка для глаз.

    Глазами следят за движениями воздушных шариков.

    Творческое применение и добывание знаний в новой ситуации (проблемные задания)

    Предлагает применить полученные знания по теме «Действия с десятичными дробями» при решении задач с помощью уравнений.

    Просит записать задачу так, чтобы учащиеся смогли ответить на вопросы после того, как текст задачи будет убран с экрана.

    1. Предлагает ученикам кратко записать условие задачи, в виде схемы в тетради.

    2. Предлагает поиск пути решения задачи и составление плана её решения.

    3.Предлагает сделать проверку, обращает внимание на подчёркнутые числа в презентации.

    Просит поделиться своими соображениями учеников.

    Отвечают на вопросы учителя.

    Выполняют краткую запись.

    Проверяют краткую запись по презентации.

    Предполагаемый правильный ответ:

    Поскольку одна из нужных нам величин для решения задачи неизвестна. Решаем задачу с помощью уравнения.

    Поочерёдно объясняют ход составления уравнения к задаче.

    Составленное уравнение один ученик пишет на доске.

    Решают уравнение в тетради. Один ученик у доски.

    Проверяют по презентации.

    Предполагаемый правильный ответ:

    Четыре одинаковых слагаемых можем заменит умножением.

    Выполняют физкультминутку, повторяя движения мультипликационных героев.

    Предлагает самостоятельно записать краткую запись задачи, составить уравнение и решить в тетради.

    Учитель записывает решение задачи под диктовку учащихся на доске,

    Учащиеся, по одному, комментируют решение задачи, обращая внимание на правила сложения, умножения десятичных дробей.

    Рефлексия (подведение итогов занятия)

    Оценка работы учащихся. Выставление оценок.

    Подведение итогов соревнования между командами Ромашка и Колокольчик.

    Просит выслать фото классной работы на почту или в ватсап.

    Обращается к учащимся:

    Наш урок подходит к концу. Скажите, вы не изменили своего мнения, по поводу отгадки кроссворда в начале урока? Подумайте о том, как всѐ происходило, что ты узнал и что ещѐ предстоит узнать?

    Сегодня я узнал(а).

    На этом уроке мне было интересно.

    Сегодня я научился(научилась).

    Мне ещѐ предстоит научиться.

    Тяжело ли было работать дистанционно?

    Когда интереснее на уроках?

    Примечание: Детям можно рекомендовать задание в учи ру «Решение текстовых .задач»

    Ученики, поднимают ладошку.

    Высказывают своё мнение.

    Как решать задачи уравнения с десятичными дробями

    Курс повышения квалификации

    Дистанционное обучение как современный формат преподавания

    • Сейчас обучается 945 человек из 80 регионов

    Как решать задачи уравнения с десятичными дробями

    Курс профессиональной переподготовки

    Математика: теория и методика преподавания в образовательной организации

    • Сейчас обучается 687 человек из 75 регионов

    Как решать задачи уравнения с десятичными дробями

    Курс повышения квалификации

    Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

    • Сейчас обучается 315 человек из 69 регионов

    Ищем педагогов в команду «Инфоурок»

    Видео:КАК РЕШИТЬ УРАВНЕНИЕ С ДЕСЯТИЧНЫМИ ДРОБЯМИ? Примеры | МАТЕМАТИКА 5 классСкачать

    КАК РЕШИТЬ УРАВНЕНИЕ С ДЕСЯТИЧНЫМИ ДРОБЯМИ? Примеры | МАТЕМАТИКА 5 класс

    Дистанционные курсы для педагогов

    «Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

    Свидетельство и скидка на обучение каждому участнику

    Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

    5 593 013 материалов в базе

    Материал подходит для УМК

    Как решать задачи уравнения с десятичными дробями

    «Математика», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

    § 34. Умножение десятичных дробей

    Самые массовые международные дистанционные

    Школьные Инфоконкурсы 2022

    33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

    «Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

    Свидетельство и скидка на обучение каждому участнику

    Другие материалы

    • 18.05.2020
    • 139
    • 5

    Как решать задачи уравнения с десятичными дробями

    • 04.05.2020
    • 413
    • 44

    Как решать задачи уравнения с десятичными дробями

    • 15.04.2020
    • 126
    • 1

    Как решать задачи уравнения с десятичными дробями

    • 02.04.2020
    • 1684
    • 457

    Как решать задачи уравнения с десятичными дробями

    • 02.04.2020
    • 280
    • 3

    Как решать задачи уравнения с десятичными дробями

    • 02.04.2020
    • 378
    • 3

    Как решать задачи уравнения с десятичными дробями

    • 01.04.2020
    • 381
    • 25

    Как решать задачи уравнения с десятичными дробями

    • 30.03.2020
    • 230
    • 1

    Как решать задачи уравнения с десятичными дробями

    Вам будут интересны эти курсы:

    Оставьте свой комментарий

    Авторизуйтесь, чтобы задавать вопросы.

    Добавить в избранное

    • 21.05.2020 554
    • PPTX 20.1 мбайт
    • 27 скачиваний
    • Оцените материал:

    Настоящий материал опубликован пользователем Смирнова Светлана Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

    Автор материала

    Как решать задачи уравнения с десятичными дробями

    • На сайте: 6 лет и 3 месяца
    • Подписчики: 0
    • Всего просмотров: 3490
    • Всего материалов: 6

    Московский институт профессиональной
    переподготовки и повышения
    квалификации педагогов

    Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

    Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.

    Дистанционные курсы
    для педагогов

    663 курса от 690 рублей

    Выбрать курс со скидкой

    Выдаём документы
    установленного образца!

    Как решать задачи уравнения с десятичными дробями

    Учителя о ЕГЭ: секреты успешной подготовки

    Время чтения: 11 минут

    Как решать задачи уравнения с десятичными дробями

    Приемная кампания в вузах начнется 20 июня

    Время чтения: 1 минута

    Как решать задачи уравнения с десятичными дробями

    Курские власти перевели на дистант школьников в районах на границе с Украиной

    Время чтения: 1 минута

    Как решать задачи уравнения с десятичными дробями

    Минпросвещения упростит процедуру подачи документов в детский сад

    Время чтения: 1 минута

    Как решать задачи уравнения с десятичными дробями

    В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

    Время чтения: 0 минут

    Как решать задачи уравнения с десятичными дробями

    В приграничных пунктах Брянской области на день приостановили занятия в школах

    Время чтения: 0 минут

    Как решать задачи уравнения с десятичными дробями

    Каждый второй ребенок в школе подвергался психической агрессии

    Время чтения: 3 минуты

    Подарочные сертификаты

    Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

    Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

    📹 Видео

    Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).Скачать

    Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).

    426 Математика 6 класс. Решите уравнение с десятичными дробямиСкачать

    426 Математика 6 класс. Решите уравнение с десятичными дробями

    УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

    УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ #егэ #егэ #математика #профильныйегэ #shorts #образование

    Действия с десятичными дробями 😈Скачать

    Действия с десятичными дробями 😈

    Решение уравнений и пропорций с десятичными дробямиСкачать

    Решение уравнений и пропорций с десятичными дробями

    Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

    Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?

    5 класс. Задача №1 на движение. "Умножение и деление десятичных дробей"Скачать

    5 класс. Задача №1 на движение. "Умножение и деление десятичных дробей"
    Поделиться или сохранить к себе: