Как решать уравнения сравнения по модулю (6 видео)

Сравнение чисел по модулю

Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.

Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде

a=sp+r,

(1)

где s — число, и r одно из чисел 0,1, . p−1.

1 ) В данной статье под словом число будем понимать целое число.

Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа

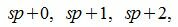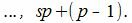Как решать уравнения сравнения по модулю

Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.

Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s₁p+r₁. Тогда

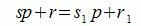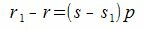(2)

Так как r₁ принимает один из чисел 0,1, . p−1, то абсолютное значение r₁−r меньше p. Но из (2) следует, что r₁−r кратно p. Следовательно r₁=r и s₁=s.

Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).

Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.

Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда

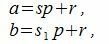где s и s₁ некоторые целые числа.

Разность этих чисел

(3)

делится на p, т.к. правая часть уравнения (3) делится на p.

Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.

Доказательство. Обозначим через r и r₁ остатки от деления a и b на p. Тогда

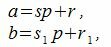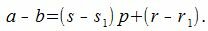По утверждению a−b делится на p. Следовательно r−r₁ тоже делится на p. Но т.к. r и r₁ числа 0,1. p−1, то абсолютное значение |r−r₁| Свойство 1. Для любого a и p всегда

a≡a mod (p).

Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если

a≡b mod (p), b≡c mod (p).

a≡c mod (p).

Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.

a≡b mod (p) и m≡n mod (p),

a+m≡b+n mod (p) и a−m≡b−n mod (p).

Действительно. Так как a−b и m−n делятся на p, то

(a−b)+ (m−n)=(a+m)−(b+n) ,

(a−b)−(m−n)=(a−m)−(b−n)

также делятся на p.

Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.

a≡b mod (p) и m≡n mod (p),

am≡bn mod (p).

Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно

am≡bm mod (p).

Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит

bm≡bn mod (p).

Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).

a≡b mod (p).

a k ≡b k mod (p).

где k некоторое неотрицательное целое число.

Действительно. Имеем a≡b mod (p). Из свойства 4 следует

a·a≡b·b mod (p).

a·a·a≡b·b·b mod (p).

a k ≡b k mod (p).

Все свойства 1-5 представить в следующем утверждении:

Утверждение 4. Пусть f(x₁, x₂, x₃, . ) целая рациональная функция с целыми коэффициентами и пусть

a₁≡b₁, a₂≡b₂, a₃≡b₃, . mod (p).

f(a₁, a₂, a₃, . )≡f(b₁, b₂, b₃, . ) mod (p).

При делении все обстоит иначе. Из сравнения

am≡bm mod (p)

не всегда следует сравнение

a≡b mod (p).

Утверждение 5. Пусть

am≡bm mod (p),

a≡b mod (p/λ),

Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда

m=m₁λ и k=k₁λ.

Так как m(a−b) делится на k, то

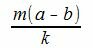имеет нулевой остаток. Тогда

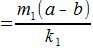имеет нулевой остаток, т.е. m₁(a−b) делится на k₁. Но числа m₁ и k₁ числа взаимно простые. Следовательно a−b делится на k₁=k/λ и, тогда, a≡b mod (p/λ).

Утверждение 6. Если

a≡b mod (p)

и m является один из делителей числа p, то

a≡b mod (m).

Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.

Утверждение 7. Если

a≡b mod (p), a≡b mod (q), a≡b mod (s)

a≡b mod (h),

где h наименьшее общее кратное чисел p,q,s.

Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.

В частном случае, если модули p,q,s взаимно простые числа, то

a≡b mod (h),

Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.

Содержание

Функции для решения квадратичных сравнений. Реализация в MATLAB
Введение
Функция для решения сравнений по сложному модулю
Функция для решения квадратичного сравнения по простому модулю
Разложение числа на множители
Вычисление значения символа Лежандра
Возведение числа в степень по методу квадрирования
Решение линейных сравнений
Конспект «теория сравнения по модулю»
📹 Видео

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Функции для решения квадратичных сравнений. Реализация в MATLAB

Введение

Для решения криптографических задач необходимо уметь решать квадратичные сравнения по заданному модулю. Алгоритм решения квадратичного сравнения достаточно прост и не вызывает сложностей в решении при небольших значениях модуля и свободного члена, однако в связи с применением достаточно больших чисел в криптографии, решение квадратичных сравнений вручную является весьма кропотливым и длительным процессом. Конечно, для решения квадратичных сравнений можно воспользоваться онлайн-сервисом. Но так как решение криптографической задачи не заканчивается на решении квадратичного сравнения, то человеку, занимающемуся криптографией, будет удобно иметь функцию, способную решать квадратичные сравнения и свободно взаимодействовать с другими функциями, которые используются ним. Именно поэтому было решено написать функцию для решения квадратичных сравнений вида x^2 ≡ a ( mod p ), где a и p — взаимно простые числа, в MATLAB.

Сразу замечу, так написание функций для решения квадратичных сравнений носило обучающий характер, некоторые пользовательские функции, используемые при вычислении, дублируют функции, уже имеющиеся в среде MATLAB.

Сначала предлагаю рассмотреть код двух главных функций, одна из которых предназначена для решения квадратичных сравнений по составному модулю, а вторая – для решения квадратичных сравнений по простому модулю. При этом мы ознакомимся, в первую очередь с алгоритмом решения квадратичных сравнений, а уже во вторую очередь с функциями, которые необходимы для выполнения самих вычислений.

Функция для решения сравнений по сложному модулю

Данная функция позволяет решать квадратичные сравнения, как по простому, так и по сложному модулю. При вызове функции в нее необходимо передать две переменные а и р, в результате своего выполнения функция вернет вектор – строку из двух противоположных по знаку решений квадратичного сравнения.

Следующим шагом в решении квадратичного сравнения будет определение типа модуля р. Для этого будет использоваться пользовательская функция factorization, предназначенная для разложения числа на простые множители. Кроме вектора-строки с простыми множителями функция возвращает количество простых множителей. По сути функция factorization дублирует стандартную функцию MATLAB factor.

После того как модуль был разложен на множители с помощью условного оператора осуществляется проверка количества множителей. Если количество множителей превышает 1, то есть модуль р – составное число, то тогда нам необходимо решить систему из sp квадратичных сравнений ( в каждом из сравнений модулем будет служить один из множителей составного модуля р ). Перед тем как браться за решение полученной системы квадратичных сравнений, необходимо убедиться в том, что каждое из квадратичных сравнений этой системы имеет решение. Для этого воспользуемся циклом for, который будет осуществлять переход между элементами вектора с множителями mp. В теле цикла будет вызываться функция, выполняющая вычисление значения символа Лежандра для каждой пары чисел.

Если значения символа Лежандра будет равно 1, то переменная count будет увеличена на 1. Это нужно для того, чтобы после выполнения всех итераций цикла мы могли проверить, все ли уравнения системы имеют решение, ведь от этого зависит, будем ли мы решать квадратичные сравнения из которых состоит система, или выведем сообщения о том, что исходное квадратичное сравнение не имеет решений.

Если количество уравнений системы равняется количеству уравнений, имеющих решения, то создаются векторы-строки для хранения промежуточных результатов вычисления.

С помощью цикла for, осуществляется переход между множителями модуля р. В вектор-строку answer1 записываются результаты решения квадратичного сравнения по простому модулю, который получен с помощью функции sqcom, в которую были переданы значение переменной а, а также значение i-ого множителя модуля p. В вектор-строку modul записывается частное от деления составного модуля р на i-ый множитель модуля p. В вектор-строку answer2 будет сохраняться результат решения линейного неравенства ( p / p( I ) ) * y ≡ 1 ( p ( i) ), которое будет необходимо для расчета окончательного ответа по формуле полученной из Китайской теоремы.

После того как цикл закончил свое выполнение, необходимо рассчитать окончательный ответ по формуле: x=( ( p / p( 1)) * b( 1 ) * y( 1 ) + ( ( p / p( 2) ) * b( 2 ) * y( 2 ) + ( ( p / p( i ) ) * b( i ) * y( i ). Для этого воспользуемся поэлементным умножением. В результате будет получена вектор-строка, сумму элементов которой найдем с помощью команды sum. Найдем остаток от деления суммы на составной модуль р – это будет одним из решений квадратичного сравнения по составному модулю. Второй ответ получим, записав первый ответ с противоположным знаком.

В том случае, если изначально модуль р оказался простым числом, то решение квадратичного сравнения будет получено, путем одноразового вызова функции для решения квадратичного сравнения — sqcom. Второе решение будет получено путем взятия первого ответа с противоположным знаком.

Ниже привожу код функции sqcomdif полностью.

Функция для решения квадратичного сравнения по простому модулю

Эта функция неоднократно вызывалась в функции sqcomdif, и как уже говорилось, функция sqcom применяется для решения квадратичного сравнения по простому модулю и может вызываться независимо от функции sqcomdif, то есть ее можно без проблем вызвать и получить верный ответ в том случае, когда вы уверенны, что модуль – простое число. Так как рассматривается лишь лишение квадратичных сравнений вида x^2 ≡ a ( mod p ), то в функцию необходимо передать числовые значения переменных а и р. В результате работы функции будет получено одно решение квадратичного сравнения.

Так как функция sqcom может использоваться отдельно от функции sqcomdif, то необходимо убедиться в том, что число, записанное в переменную а, является квадратичным вычетом модуля р. Для этого воспользуемся функцией symvol, которая позволяет вычислить значение символа Лежандра для указанной пары чисел.

Если значение переменной Symvol_Lejandra равно 1, то а является квадратичным вычетом по модулю р и будут выполнены дальнейшие действия для нахождения решения квадратичного сравнения. Нам нужно записать число ( р – 1 ) в виде 2^r * q. Начальные значения переменным r, q задаются из расчета, что ( р – 1 ) – нечетное число. Однако если это не так, то они будут изменяться в процессе выполнения цикла ( до тех пор, пока q не станет нечетным числом ).

Теперь необходимо найти значение переменной b, которая равняется b = a^q ( mod p ). Так как а и q, обычно выражены достаточно большими числами, то возвести число а в степень q обычным способом не удастся, так как в большинстве случаев возникнет переполнение. Поэтому возведение в степень необходимо выполнять по методу квадрирования. Для того чтобы выполнить это необходимо вызвать функцию kvadrirovanie и передать в нее значение основания, показателя степени, а также модуля по которому будут выполняться вычисления.

Для продолжения вычислений нужно найти наименьшее неотрицательное число f, которое будет квадратичным невычетом по модулю р. Для этого переменной f, присваивается значение 1, и с помощью функции symvol, определяется значение символа Лежандра для пары чисел f и р. Если символ Лежандра для 1 и р равен 1, то переменная f, с помощью цикла while, увеличивается, до тех пор, пока не будет достигнуто значение, являющееся квадратичным невычетом по модулю р.

Теперь значение f, являющееся квадратичным невычетом по модулю p, необходимо возвести в степень q. Для этого также придется прибегнуть к функции kvadrirovanie, переменной k не обходимо присвоить значение 0.

После вышеперечисленных действий необходимо проверить значение переменной b. Если b сравнимо с 1 по модулю p, то необходимо перейти к расчету ответа, в противном случае найти наименьшее неотрицательное число m, такое что b^( 2^m ) ≡ 1 ( mod p ). Когда такое значение m будет найдено, необходимо пересчитать значения переменных k, g, b, после чего переменной r присвоить значение m. Но это еще не все, необходимо проверить, чтобы новое значение переменной b, также было сравнимо с 1 по модулю р. Если это не так, то необходимо вернуться к подбору числа m. Переменная pok нужна для того, чтобы избежать выполнения определенных математических действий дважды.

После того как было найдено m, удовлетворяющее перечисленным выше условиям, можно переходить к непосредственному вычислению ответа. Ответ вычисляется по формуле x = a^( ( q+1) / 2 ) * g^( k / 2 ) ( mod p ). Для вычисления обеих множителей воспользуемся функцией квадрирования, полученный результат возьмем по модулю p.

Полученный результат не всегда может быть записан оптимально, по модулю р. Поэтому необходимо выполнить следующую проверку:

Ниже приведен полный код функции sqcom:

А теперь предлагаю ознакомиться с вспомогательными функциями, которые используются как при решении квадратичного сравнения, так могут использоваться и отдельно.

Разложение числа на множители

При решении квадратичного сравнения во многих случаях необходимо прибегать к разложению числа на множители, также к этой операции придется прибегать в тех случаях, когда будет необходимо проверить: является число простым или составным.
В функцию factorization передается число, которое необходимо разложить на множители. В результате функция возвращает вектор — строку с множителями и количество этих множителей.

Функция состоит из оператора switch, который выполняет различные действия в зависимости от значения входной переменной delimoe. Так если delimoe = 1, то в вектор, хранящий результат разложения на множители, mnojitel записывается 1, в переменную ind, хранящую число множителей, также записывается 1. Аналогичные действия выполняются и в том случае, если delimoe равно -1.

Если эти условия не выполнились, то выполняем проверку знака числа, раскладываемого на множители. Если delimoe меньше 0, то в первый множитель записывается -1, в ind записывается 2, и дальнейшая работа функции будет осуществляться с модулем переменной delimoe.Если же число больше 0, то переменной ind присваивается значение 1.

Цикл while работает до тех пор, пока delimoe не равняется delitel, причем изначально переменной delitel присвоено значение 2. При каждой итерации цикла, в переменную ostatok записывается остаток от деления delimoe на delitel. Если остаток равен 0, то есть delitel является множителем delimoe, то это значение записывается в вектор, в котором хранятся множители, а счетчик этого вектора увеличивается на 1. При этом переменной delimoe присваивается частное от выполненного деления. Если же остаток от деления не равен 0, то delitel увеличивается на 1. Когда же происходит выход из цикла, то значение, оставшееся в переменной delimoe, записывается в вектор с множителями, как один из множителей.

Ниже приведу полный код функции factorization.

Вычисление значения символа Лежандра

Для того чтобы проверить является ли число квадратичным вычетом по заданному модулю ( в таком случае квадратичное сравнение имеет решение ) или квадратичным невычетом ( тогда такое квадратичное сравнение не имеет решения ) применяется символ Лежандра, который в отечественной литературе обозначается как L ( a; p ), в зарубежной литературе как L (a / p ).
Символ Лежандра может принимать следующие значения:
L ( a; p ) = 1, в таком случае а принадлежит QR, квадратичное сравнение имеет решение
L ( a; p ) = -1, в таком случае а принадлежит QNR, квадратичное сравнение не имеет решения
Если L ( a; p ) = 0, то а и р не являются взаимно простыми числами, то есть НОД ( а; р ) не равен 1
Для вычисления значения символа Лежандра применяются следующие свойства:

L ( 1; p ) = 1
L ( -1; p ) = ( -1 ) ^ ( ( p — 1 ) / 2 )
L ( 2; p ) = ( -1 ) ^ ( ( p^2 — 1) / 8 )
Если а≡ b*с ( mod p ), то L ( b*с; p ) = L ( b; p ) * L (с; p )
Если а≡ b ( mod p ), то L ( а; p ) = L ( b; p )
Если а и р – простые числа, то L ( а; p ) = (-1) ^( (( p — 1 ) *(a-1)) / 4 ) * L( p; a ). Последнее свойство получило название закона взаимности Гаусса.

Вычисление символа Лежандра выполняется на основе вышеперечисленных свойств. Как только одно из условий выполнилось, начинаем проверять свойства для полученной пары а и р, до тех пор, пока не будет найдено окончательное значение символа Лежандра.
Теперь рассмотрим, как можно реализовать вычисление значения символа Лежандра программно.
Функция будет возвращать значение символа Лежандра для пары чисел а и р, которые были переданы в нее. Это видно из заголовка функции:

Следующий шаг по своей сути является применением свойства 5. Если число а больше модуля р, то его можно заменить меньшим числом, сравнимым с а по модулю р.

Полученное число а, пытаемся разложить на множители. Для разложения числа на множители была написана пользовательская функция factorization, возвращающая вектор с простыми множителями, из которых состоит число а, а также их количество. Подробно эта функция была описана выше.

Если а не являлось простым числом, то будем действовать по свойству 4. То есть значение символа Лежандра для пары чисел L ( а; p ), найдем как произведение значений символов Лежандра для чисел, являющихся простыми множителями числа а. Для хранения промежуточных результатов создадим вектор-строку, заполненную нулями с размерностью, равной количеству множителей числа а. Если а – простое, то эта строка будет состоять из одного элемента.

Для вычисления символа Лежандра для каждого множителя поочередно воспользуюсь циклом for, который будет изменять свои значения от 1 до номера последнего множителя. В теле данного цикла происходит непосредственный процесс вычисления значения символа Лежандра с помощью свойств, перечисленных выше.
Код для проверки свойства 1 имеет следующий вид:

Так как при проверке значения символа при его виде L(-1,p), по свойству 2, необходимо вычислить значение ( -1 ) ^ ( ( p — 1 ) / 2 ), то необходимо воспользоваться еще одним условным оператором, в котором будет проверяться, является показатель -1 четным или нечетным числом. В зависимости от этого будет варьироваться значение символа Лежандра. Если показатель четный – то символ Лежандра будет равен 1, в противном случае -1. Применение этого условного оператора позволяет избежать возведение -1 в степень ( р — 1)/2, что является весьма затратной операцией.

Аналогичные действия выполняются и в том случае, когда необходимо вычислить значение символа Лежандра при его виде L ( 2; p ). В таком случае оно будет равняться ( -1 ) ^ ( ( p^2 — 1) / 8 ).

После проверки этого условия число а, передается в функцию, для того, чтобы проверить, простое оно или нет. В случае если число а – составное ( число его множителей ind1 больше 1 ), то происходит рекурсия и число а передается в эту же функцию для выполнения дальнейших вычислений.

В противном случае число а – простое. Если при этом оно не равно -1, 1, 2, то приходится воспользоваться свойством 6 – законом взаимности Гаусса. Знак перед символом Лежандра определяется путем определения четности множителей его показателя. Он обращается в плюс, если хотя бы один из множителей – четный. После чего происходит рекурсивный вызов функции symvol, а аргументы в нее передаются в другом порядке.

В результате проверки вышеперечисленных условий были охвачены все возможные варианты значений числа а.
Если изначально число а было составным, то в переменную sl записывается произведение всех элементов строки — вектора sl, после чего полученное значение возвращается в программу, вызвавшую данную функцию.

Полный код функции symvol:

Возведение числа в степень по методу квадрирования

При решении квадратичного сравнения часто приходится сталкиваться с необходимостью возведения больших чисел в степень с показателем равным нескольким сотням, а то и тысячам. При обычном возведении числа в такую степень достаточно легко натолкнуться на такое неприятное явление, как переполнение. Для того чтобы избежать его, необходимо возводить такие числа в степень используя метод квадрирования.
Рассмотрим алгоритм данного метода:

Показатель степени записывается в двоичной системе счисления.
Если он состоит из двух или более бит, под первой 1 записываем число m=a.
Смотрим на следующий справа бит:
- Если это единица то возводим m в квадрат и берем его по модулю р, а полученный результат домножаем на а и берем его по модулю р, окончательный результат записывается в переменную m.
- Если это нуль, то возводим число m в квадрат, берем результат по модулю р, окончательный результат записывается в переменную m.
Переходим к следующему справа биту и повторяем действия описанные в пункте 3, пока не будут выполнены расчеты для последнего бита.

А теперь рассмотрим, как работает функция kvadrirovanie. В функцию передаются значения основания, показателя и модуля, а возвращает функция одно число – конечный результат.

Показатель степени q переведем в двоичный вид, и так как полученный результат будет состоять из отдельных символов, то воспользуемся командой size, для определения количества бит, необходимых для записи показателя степени.

Если для записи показателя степени необходимо два или более битов, то программа выполнит следующие действия: запишет в переменную m типа uint64 число а. После чего с помощью цикла for, который будет изменять значения переменной i от 2 с шагом 1 до количества бит, необходимых для записи показателя степени q, для того, чтобы иметь возможность осуществлять перебор битов.

В теле цикла имеется условный оператор, который, в зависимости от значения i-го бита, будет определять действия, которые необходимо произвести с переменной m. Как писалось выше, если бит равен 1, то необходимо возвести m^2 и взять по модулю р, после чего умножить полученное число на а, и результат взять по модулю р.

Иначе, q(1,i)==’0′, необходимо возвести m^2 и взять его по модулю р.

После выполнения всех повторов цикла, окончательное значение переменной m записывается в переменную result.

В показатель степени в двоичной форме равен 1, то в переменную result записывается само же исходное число, которое требовалось возвести в степень.

Если же и это условие не выполнилось, то следовательно показатель степени равняется 0. В таком случае в переменную result будет записана 1.

Полный код функции для возведения в степень по методу квадрирования:

Решение линейных сравнений

При решении квадратичных сравнений по сложному модулю будет применяться формула, полученная из Китайской теоремы. Для того чтобы рассчитать ответ по этой формуле появляется необходимость решить линейное сравнение k * x ≡ b ( mod p ). Данная функция предназначается для их решения с помощью обратного элемента, то есть такого числа k1 которое при умножении на k, даст результат сравнимый с 1 по заданному модулю р.
В функцию lincom передаются значения коэффициента при неизвестном k, число b, с которым сравнима левая часть, а также модуль p, а возвращает функция соответственно решение линейного сравнения с заданными параметрами.

Как указывалось выше, неравенство будем решать с помощью обратного элемента. Для того чтобы найти обратный элемент воспользуемся расширенным алгоритмом Эвклида для нахождения НОДа. Напомню, что расширенный алгоритм Эвклида позволяет найти НОД с помощью коэффициентов, которые рассчитываются при выполнении каждой операции деления. Для нахождения НОДа по данному алгоритму необходима рассчитать два ( a, b ) коэффициента, но при нахождении обратного элемента нам потребуется только один – b коэффициент, который как раз и будет обратным элементом для k.
В функции необходимо указать начальные значения коэффициентов b0 и b1, которые будут изменяться по мере выполнения расчетов. Если модуль p, который был записан в переменную pr, делится нацело на коэффициент k, то обратный элемент будет равен 1. Иначе b1 будет рассчитываться с помощью цикла while. В цикле будет пересчитываться значения переменной b0. После того как найдено новое значение b0, с помощью функции swap будет осуществляться обмен значений между переменными b0 и b1. Также при каждой итерации цикла будет происходить присвоение новых значений ряду других переменных.

После того, как цикл прекратит свое выполнение будет необходимо рассчитать значение решения линейного сравнения. Оно будет равно произведению переменных b1 и b, взятое по модулю p ( именно для этой операции в начале функции значение модуля было продублировано с помощью переменной pr ).

Видео:✓ Сравнение по модулю. Арифметика остатков | Ботай со мной #034 | Борис ТрушинСкачать

Конспект «теория сравнения по модулю»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Муниципальное бюджетное общеобразовательное учреждение

Семлевская средняя общеобразовательная школа №1

Вяземского района Смоленской области

Научно-исследовательская работа по теме
«Теория сравнения по модулю»

Подготовила
ученица 9 класса: Попова Анастасия

Преподаватель: Перцева С.М.

Понятие модуля числа известно каждому, а вот что означает понятие сравнение по модулю, знают далеко не все. Тема моей работы «Теория сравнения по модулю». Я обратилась к этой теме, так как она недостаточно полно изложена в действующих учебниках математики, а задачи по этой теме предлагаются как на олимпиадах, так и на вступительных экзаменах в вузы.

Цель работы : разобраться с понятием «сравнение по модулю», развить умение применять знания в решении практических заданий .

1) Изучить краткий исторический обзор возникновения теории;

2) Дать определение сравнения по модулю;

3) Изучить свойства сравнения по модулю;

4) Рассмотреть операции со сравнениями;

5) Применить знания для решения практических заданий.

1)Теоретический анализ и обобщение научной литературы;
2)Математический расчет;

1.Историческая справка . Предпосылкой к созданию теории сравнений стало восстановление сочинений Диофанта, которые были выпущены в подлиннике и с латинским переводом, благодаря Баше де Мезириаку, в 1621. Их изучение привело Ферма́ к открытиям, которые по значению существенно опередили свое время. Этой же темой независимо от Ферма занимался Лейбниц. Позже изучение вопросов теории сравнений, было продолжено Эйлером. Утвердившуюся в математике символику предложил Гаусс. Он же впервые использовал сравнения по модулю в своей книге «Арифметические исследования» в 1801 году. Гаусс преобразовал все накопленные до него сведения, связанные с операциями сравнения по модулю, в стройную теорию, которая и была впервые изложена в этой книге.

Теорию сравнения по модулю называют модульной арифметикой. В математике модульная арифметика — система арифметики для целых чисел, где числа «обертывают вокруг» после достижения определенной стоимости — модуль . Знакомое использование модульной арифметики находится в 12-часовых часах , в которых день разделен на два 12-часовых периода. Если время будет 7:00 теперь, то 8 часов спустя это будет 3:00. Обычное дополнение предложило бы, чтобы более позднее время было 7 + 8 = 15, но это не ответ, потому что время часов «обертывает вокруг» каждые 12 часов; в 12-часовое время нет никаких «15 часов». Аналогично, если запуски часов в 12:00 (полдень) и 21 час протекут, то время будет 9:00 на следующий день, а не 33:00. Так как число часа начинается после того, как оно достигает 12, это — арифметический модуль 12. Согласно определению ниже, 12 подходящее не только 12 самому, но также и 0, таким образом, время, названное «12:00», можно было также назвать «0:00», так как 12 подходящее 0 модулям 12.

Если два целых числа и при делении на дают одинаковые остатки, то они называются сравнимыми по модулю числа .