Как решать уравнения с умножением и сложением (3 видео)

Содержание

Методы решения систем уравнений с двумя переменными
п.1. Метод подстановки
п.2. Метод сложения
п.3. Метод замены переменных
п.4. Графический метод
п.5. Примеры
Системы уравнений
Способ подстановки
Способ сравнения
Способ сложения или вычитания
Простые уравнения на умножение и деление. 2 класс.
📽️ Видео

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Методы решения систем уравнений с двумя переменными

п.1. Метод подстановки

Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.

Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.

п.2. Метод сложения

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.4. Графический метод

Графический метод подробно рассмотрен в §15 данного справочника.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) ( left< begin mathrm & \ mathrm & endright. )
Решаем методом подстановки: ( left< begin mathrm & \ mathrm & endright. )
Для нижнего уравнения: ( mathrm )
Подставляем в верхнее уравнение: ( mathrm )

б) ( left< begin mathrm & \ mathrm & endright. )
Замена переменных: ( left< begin mathrm & \ mathrm & endright. )
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: ( left< begin mathrm & \ mathrm & endright.Rightarrow left< begin mathrm & \ mathrm & endright. )
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ mathrm< D=9^2-4cdot 2cdot 10=1, b=frac> = left[begin mathrm & \ mathrm & endright. $$ Возвращаемся к исходным переменным: ( left[begin left<begin mathrm & \ mathrm & endright.& \ left<begin mathrm & \ mathrm & endright. endright. )

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Системы уравнений

Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:

	x — 4y = 2
	3x — 2y = 16

Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.

Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Способ подстановки

Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.

Рассмотрим решение системы уравнений:

	x — 4y = 2
	3x — 2y = 16

Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:

Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:

3x	— 2y = 16;
3( 2 + 4y )	— 2y = 16.

Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.

3(2 + 4y) — 2y = 16;

6 + 12y — 2y = 16;

6 + 10y = 16;

10y = 16 — 6;

10y = 10;

y = 10 : 10;

y = 1.

Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:

x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Способ сравнения

Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.

Например, для решение системы:

	x — 4y = 2
	3x — 2y = 16

найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):

x — 4y = 2	3x — 2y = 16
-4y = 2 — x	-2y = 16 — 3x
y = (2 — x) : — 4	y = (16 — 3x) : -2

Составляем из полученных выражений уравнение:

2 — x	=	16 — 3x
-4	=	-2

Решаем уравнение, чтобы узнать значение x:

2 — x	· (-4) =	16 — 3x	· (-4)
-4		-2

2 — x = 32 — 6x

—x + 6x = 32 — 2

5x = 30

x = 30 : 5

x = 6

Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:

x — 4y = 2	3x — 2y = 16
6 — 4y = 2	3 · 6 — 2y = 16
-4y = 2 — 6	-2y = 16 — 18
-4y = -4	-2y = -2
y = 1	y = 1

Видео:Решение сложных уравнений 4-5 класс.Скачать

Способ сложения или вычитания

Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.

	x — 4y = 2
	3x — 2y = 16

Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:

	x — 4y = 2
	-6x + 4y = -32

Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:

+	x — 4y = 2
+	-6x + 4y = -32
-5x = -30

Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.

Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.

Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:

(x — 4y) · 3 = 2 · 3

	3x — 12y = 6
	3x — 2y = 16

Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:

—	3x — 12y = 6
—	3x — 2y = 16
-10y = -10

Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:

3x — 2y = 16

3x — 2 · 1 = 16

3x — 2 = 16

3x = 16 + 2

3x = 18

x = 18 : 3

x = 6

Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:

Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.

Видео:Решение уравнений на умножение и деление.Скачать

Простые уравнения на умножение и деление. 2 класс.

Большие затруднения для младшего школьника вызывает умение решать данный вид уравнений.

Мы уже знаем, что простые уравнения – это равенства, где есть одна переменная (неизвестное число).

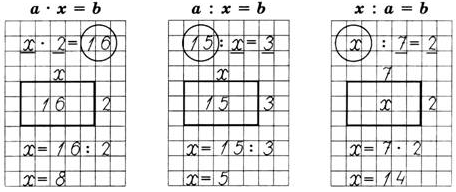
Во 2 классе дети учатся решать простые уравнения на умножение и деление (5 • х = 10, х: 3 = 12, 12 : х = 4)
Для решения этих уравнений правила о части и целом использовать нельзя, потому что второй множитель (х • 3 = 12) — это не часть, а число равных частей, на которое разбили целое.

Сегодня мы рассмотрим несколько вариантов решения:

Как никогда не путаться в выборе действий.

Если вы видите уравнение х: 4 = 8 и сомневаетесь, нужно х = 8 • 4 или х = 8 : 4, поступайте так: пишите на черновике простой пример на то действие, которое хочет вас запутать. Действие у нас – деление. Давайте напишем 6 : 2 = 3 и закроем число, которое в нашем уравнении неизвестно — это первое число, значит, закрываем число 6. И как шестерку найти, имея 2 и 3? Надо – перемножить тройку с двойкой. Значит, и в нашем уравнении нужно перемножать числа, но никак не делить:

Этот способ выручает, когда мы решаем вот такие уравнения: 4857 + у = 10208.
Большие числа часто пугают, а они живут по тем же законам, что и маленькие числа. Поэтому пишем, например 4 + 1 = 5. И закрываем число 1. Чтобы его найти, нужно из 5-и вычесть 1. Значит, 10208 – 4857:
у = 10208 — 4857
у = 5351

2. Зная правила нахождения стороны и площади прямоугольника.

3. Используя взаимосвязи между компонентами действий.

Этот способ необходим при ответе у доски.
Ученики младших классов обязаны овладеть математической речью, а для этого нужно знать, как называются компоненты при различных действиях:
Слагаемое, слагаемое, сумма.

Уменьшаемое, вычитаемое, разность.

Множитель, множитель, произведение.

Делимое, делитель, частное.

Например, в решении уравнения x • 3 = 6 объясняем так: чтобы найти первый множитель, надо значение произведения разделить на второй множитель.

В уравнении неизвестно слагаемое:

чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое:

4. Использование памятки:

х + 6 = 124 х – 3 = 71 х × 3 = 183 х : 2 = 15	Если переменная х находится вначале уравнения, то находи ее действием, противоположным тому, что в уравнении. То есть для сложения – вычитанием и наоборот. Для умножения – делением и наоборот.
12 + х = 138 146 – х = 59 30 × х = 3000 500 : х = 4	Если х находится посередине уравнения, то или вычитай, или дели.