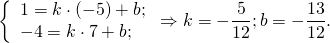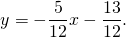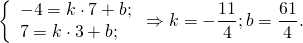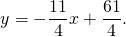Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
- Решить треугольник Онлайн по координатам
- Решение задач по геометрии 7 класс, объяснение тем, объяснение задач
- Основные темы по геометрии 7 класс
- Геометрия 7 класс объяснение основных тем, понятно для детей
- первые геометрические объекты
- О равных треугольниках. Равнобедренный треугольник
- параллельные прямые
- прямоугольный треугольник и его свойства
- Геометрия 7 класс задача по теме треугольники, пояснение решения задач
- Геометрия 7 класс тест по теме треугольник
- 7 класс геометрия сложная тема, разъяснить подробно для детей
- 📹 Видео
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать  Решение задач по геометрии 7 класс, объяснение тем, объяснение задачВ 7 классе ученики начинают изучать новый предмет — геометрию. До этого они уже знакомились с некоторыми геометрическими понятиями, но не так подробно. Чтобы в дальнейшем не возникали трудности с усвоением информации, следует с самого начала усвоить основные моменты: уметь различать типы фигур, знать основные их свойства, выучить теоремы, признаки фигур. В 7 классе изучаются простейшие объекты: точка, луч, отрезок, прямая и т.д. Кроме этого, в учебниках подробно рассматривается треугольник. Чтобы помочь ученику с усвоением основных тем по геометрии, ниже рассмотрено их содержание, представлены рисунки фигур и задачи по темам треугольников. Видео:Уравнения стороны треугольника и медианыСкачать  Основные темы по геометрии 7 классУченику 7 класса предстоит познакомиться со следующими основными разделами учебника по геометрии: Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать  Геометрия 7 класс объяснение основных тем, понятно для детейпервые геометрические объектыНачать стоит с самого понятия «геометрия». С древнегреческого слово переводится как земля и измерение. Эта древнейшая наука, которая появилась в связи с необходимостью строить здания, дороги, измерять объекты и прокладывать границы.
О равных треугольниках. Равнобедренный треугольникТреугольником принято считать фигуру, которая состоит из 3-х точек. Причем точки эти не должны лежать на одной прямой, а соединяются они отрезками.
Треугольники можно различать по двум признакам: размеру сторон и размеру углов.
Чтобы понять, равны ли треугольники, познакомимся с признаками равенства этих фигур.
Остановимся отдельно на равнобедренных треугольниках. Если 2 стороны треугольники равны, то его называют равнобедренным.
параллельные прямые
Чтобы понять, параллельны ли прямые, нужно усвоить 3 основных признака.
прямоугольный треугольник и его свойстваПрямоугольным называют треугольник, в котором один из углов равен 90º. Рассмотрим название сторон такой фигуры.
Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать  Геометрия 7 класс задача по теме треугольники, пояснение решения задачРешим несколько задач про треугольники:
Сумму периметра АВС также записали с помощью сложения сторон. Затем упростили это сложение, записав: 32 = 2 АВ + 2 ВМ (так как АВ и АС равны — равнобедренный треугольник; ВМ и СМ тоже равны). Потом эту запись сократили, разделив на 2. Вышло, что сумма двух сторон равна 16 см. Остается найти третью сторону (АМ). Она входит в треугольник АВМ, периметр которого равен 24 см. Тогда, чтобы найти третью сторону (АМ, нужно просто 24 отнять 16, вышло 8 см. В примере подставили в уравнение, чтобы не запутаться. Решим задачу на нахождение угла в треугольнике. Чтобы найти угол С в задаче потребовалось узнать, чему равен угол В. По условиям известно, что внешний В равняется 110º. Знаем, что развернутый угол равняется 180º (это внешний и внутренний угол В в сумме). Поэтому от 180 отнимаем 110. Получается угол В = 70º. Треугольник равнобедренный, значит углы при основании одинаковые ⇒ угол В = углу А = 70º. Поскольку сумма углов треугольника равна 180º (по правилу), значит угол С = 180 — углы А и В = 180 — 70 — 70 = 40°.
Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать  Геометрия 7 класс тест по теме треугольникЗакрепим материал по треугольникам, решив несколько тестовых заданий.
а) площадь; 2. Треугольник называется равнобедренным, если: а) у него есть основание; 3. Если в равнобедренном треугольнике к основанию провести высоту, то чем еще она будет являться? а) биссектрисой; 4. Сколько всего признаков равенства треугольников? 5. В треугольнике можно провести ___ медиан (-ы) а) одну; 6. Как называются стороны прямоугольного треугольника, которые образуют угол 90º? а) гипотенузы; 7. Про что гласит 3-й признак равенства треугольников? а) про стороны; 8. Под каким углом в любом треугольнике проходит высота? а) это зависит от вида треугольника 9. По каким признакам различаются виды треугольников? а) по размеру сторон; 10. Чему равна сумма двух острых углов прямоугольного треугольника? а) 90 градусов; Ответы: 1 — б; 2 — в; 3 — в; 4 — б; 5 — в; 6 — б; 7 — а; 8 — в; 9 — в; 10 — а. Видео:Задача, которую исключили из экзамена в АмерикеСкачать  7 класс геометрия сложная тема, разъяснить подробно для детейРешим более сложную задачу, где есть и доказательство равенства треугольников, и поиск углов. Алгоритм решения задачи: Шаг 1. Начертим, согласно условиям. Дается треугольник АВС, в котором провели медиану (вспоминаем, что медиана делит сторону пополам). В нашей задаче медиана AD уходит за пределы треугольника, создавая дополнительный отрезок DE (он равен AD). Получился треугольник, из которого проведена медиана. Шаг 2. Первая задача — доказать равенство треугольников ABD и ECD: соединим точку Е и С, чтобы получился треугольник. Шаг 3. По условиям AD и DE равны (одна сторона треугольника равна другой стороне ⇒ AD = DE Шаг 4. Получается BD = DC, так как медиана разделила BC пополам (выходит, еще одни стороны треугольников равны). Шаг 5. Рассмотрим углы между сторонами (на рис. обозначены цифрами 1 и 2). Они вертикальные, так как образовались двумя прямыми. Следовательно, они равны. Из первого признака равенства треугольников знаем, что если 2 стороны и угол между этими сторонами одного треугольника равен этим показателям во втором, то они равные. Пункт а доказан. Переходим к б. Шаг 1. Нам нужно найти угол АСЕ. Из рисунка видно, что он состоит из 2-х маленьких углов, получается: угол АСЕ равен сумме углов DCA и DCE. Шаг 2. По условиям мы знаем, чему равен DCA, осталось найти второй. Так как равенство треугольников доказали, значит воспользуемся правилом: напротив равных сторон треугольников лежат и равные углы. AD напротив ABD; DE напротив DCE. Выходит: угол ABD = углу DCE = 40 градусам (по условию). Шаг 3. Маленькие углы известны, найдем тот, который требуется: угол ACE = 56º + 40º = 96º. Равенство доказали, угол нашли. Задание выполнено.
Еще пара видеороликов про решение задачи с прямоугольным треугольником, а также вся геометрия за 7 класс в одной задаче. 📹 ВидеоРавнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать  ТРЕУГОЛЬНИК ПАСКАЛЯ, В УРАВНЕНИЯХСкачать  Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать  Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать  Как подготовиться к профилю за 5 месяцев? | Дмитрий НадежныйСкачать  9 класс, 15 урок, Решение треугольниковСкачать  Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать  Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать  ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать  Решение задач на тему "Подобные треугольники". 8 классСкачать  Советская олимпиада, которую сегодня решить только 2 школьниковСкачать  Признаки равенства треугольников. Практическая часть. 7 класс.Скачать  7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  | ||
