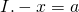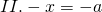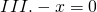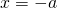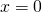Как решать уравнения с противоположными числами (4 видео)

Уравнения вида -х равен a

Уравнения вида «-x равен а» появляются в 6 классе с началом изучения отрицательных чисел.

Поскольку такие уравнения в дальнейшем будут встречаться довольно часто, желательно сразу же научиться их решать правильно и быстро.

В общем виде уравнения вида «минус икс равен а» можно разбить на три случая:

Рассмотрим каждый из вариантов в общем виде и на примерах.

Решить это уравнение — значит, найти x. x и -x — противоположные числа. Поэтому икс равен числу, противоположному числу, стоящему в правой части уравнения, то есть числу которое отличается только знаком:

Рассуждая аналогично, приходим к выводу, что

Здесь минус икс равен нулю. Нуль не является ни положительным, ни отрицательным числом и противоположен самому себе, поэтому корень этого уравнения

Итак, в общем виде решение уравнений вида минус икс равен а можно записать так:

Содержание

Математика. 6 класс
Конспект урока по математике на тему «Противоположные числа» (6 класс).
Выберите документ из архива для просмотра:
💡 Видео

Видео:Противоположные числа. Математика 6 классСкачать

Математика. 6 класс

Конспект урока

Перечень рассматриваемых вопросов:

Уравнение – равенство содержащее букву, значение которой надо найти.

Решить уравнение – значит найти все его корни.

Корнем уравнения называют такое число, при подстановке которого в уравнение вместо неизвестного, получается верное числовое равенство.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Как решаются уравнения? Чем уравнение отличается от буквенного выражения? На эти и другие вопросы, связанные с уравнениями, мы сегодня и будем отвечать.

Дадим определение уравнению. Уравнением называют равенство, содержащее букву, значение которой надо найти.

Например, 2х – 5=17.

Решить уравнение – значит найти все его корни.

В нашем случае x=11.

Подставим в уравнение корень

Получается, что левая и правая части равны семнадцати.

При решении уравнений можно использовать следующие приёмы:

– переносить числа из одной части уравнения в другую, меняя их знак на противоположный.

– делить или умножать обе части уравнения на одно и тоже число отличное от нуля.

Равенство не изменится, если к обеим частям уравнения прибавить по числу три икс:

Перенесём число 7 из левой части в правую часть уравнения с противоположным знаком:

Применим распределительный закон для правой части:

Упростим левую и правую части уравнения:

Равенство не изменится, если обе части уравнения разделить на 5:

2 ∙ (– 3) + 7 = – 3 ∙ (– 3) – 8,

Значит, корень уравнения найден верно.

Перенесём число 3 в правую часть уравнения с противоположным знаком:

Где используются уравнения?

Ответ на этот вопрос достаточно прост. Уравнения используются практически везде. В школе мы решаем с помощью уравнений текстовые задачи. В окружающем нас мире все природные и жизненные процессы протекают по определённым закономерностям, большинство из которых можно описать с помощью уравнений. Например, если нужно определить во сколько должен выехать автомобиль, чтобы прибыть вовремя из пункта А в пункт В, необходимо использовать уравнения движения. Для точного расчёта затрат и прибыли на предприятиях используют экономические уравнения. В медицине для обработки данных ультразвуковых исследований организма тоже используются уравнения.

Итак, уравнения – это универсальный инструмент для решения самых разных прикладных задач.

Разбор заданий тренировочного модуля

Тип 1.Найдите корни уравнения.

Перенесём – 5 в правую часть уравнения с противоположным знаком:

Вычислим отдельно левую и правую части уравнения.

Это и есть корень уравнения.

Тип 2. Будет ли являться корнем данного уравнения число 7?

Чтобы выполнить данное задание нужно подставить число 7 вместо неизвестного х и проверить, будут лиравны правая и левая части уравнения. Если будут равны, то число является корнем уравнения, если правая и левая части уравнения не равны, то число не является корнем уравнения.

Видно, что при подстановке в уравнение числа 7 верное равенство не получилось. Следовательно, число 7не является корнем уравнения.

Видео:Модуль числа. Практическая часть. 6 класс.Скачать

Конспект урока по математике на тему «Противоположные числа» (6 класс).

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ урок.docx

Учитель: Полякова Евгения Анатольевна.

Тема урока: Противоположные числа.

Тип урока: урок открытия нового знания.

Цель урока: через сравнение и наблюдение вывести новое понятие, учиться практически использовать противоположные числа.

Подвести учащихся к определению противоположных чисел.

Научить находить числа, противоположные данным числам; решать уравнения.

1. Способствовать развитию внимания, логики, мышления

2. Учить обобщать, сравнивать, выделять главное, переносить знания в новую ситуацию

Содействовать формированию сотрудничества, взаимоуважения

Стимулировать интерес к исследовательской деятельности

Форма урока: Форма организации урока — нестандартная форма, деловое сотрудничество

Методы обучения: словесные — беседа, практические- индуктивный, дедуктивный, проблемно- поисковый создание ситуации успеха.

Формы работы на уроке: фронтальная, индивидуальная .

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, раздаточный материал (карточки с заданием, тема урока, магнитики, плакат с формулой, с иллюстрацией НИИ), презентация.

– Виленкин, Н. Я. Математика. 6 класс : учеб. для общеобразоват. учрежд. / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – М. : Мнемозина, 2011.

Место урока в образовательной области: глава II «Рациональные числа», §5 «Положительные и отрицательные числа», пункт 27 «Противоположные числа»

Личностные УУД: формировать способность к самооценке на основе критерия успешности учебной деятельности

Регулятивные УУД: развивать умение определять и формулировать проблему урока, цель деятельности, план реализации цели, адекватно оценивать свою работу и работу своих товарищей, вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок, высказывать своё предположение.
Коммуникативные УУД: умение оформлять свои мысли в устной форме, используя математические термины, вести диалог, аргументированно высказывать свое мнение по проблеме
Познавательные УУД: формирование навыка исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания.

Планируемые результаты: учащиеся научатся различать пары противоположных чисел, использовать в практической деятельности свои знания, анализировать свои действия и управлять ими, выполнять мыслительные операции анализа и синтеза, делать умозаключения, устанавливать аналогии и причинно-следственные связи, слушать собеседника и вести диалог.