Как решать уравнения с помощью разложения на множители 7 класс

Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:

а затем каждую скобку приравнять к нулю и решить как отдельное уравнение.

Вынесем за скобку икс.

Разобьем уравнение на два простейших.

В первом корень уравнения уже понятен, во втором надо перенести (5) в правую сторону.

Решение методом разложения на множители основывается на простой идее:

В результате умножения ноль можно получить, только если один из множителей равен нулю.

Попробуйте придумать два числа, которые при умножении дают ноль. Вы убедитесь, что хотя бы одно из них обязательно должно быть нулем.

Этот метод решения уравнений один из самых популярных, поэтому освоить его очень важно для тех, кто планирует иметь четверки и пятерки. А для освоения этого метода, конечно, надо уметь раскладывать на множители как Бог: знать все формулы сокращенного умножения, легко выносить множители за скобки, уметь применять метод группировки и т.д. Подробнее о всех способах разложения на множители смотри здесь .

Пример(задание из ОГЭ). Решите уравнение (x^3+4x^2-4x-16=0).
Решение:

Перед нами кубическое уравнение.
Применим метод группировки: из первой пары слагаемых вынесем (x^2), а из второй – минус четверку.

Видео:РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

Урок по алгебре в 7-м классе по теме: «Решение уравнений с применением приемов разложения многочлена на множители»

Разделы: Математика

Ребята, достаточно долго овладевая приёмами разложения многочлена на множители, подошли к моменту, когда необходимо систематизировать и обобщить изученные способы, попытаться сделать новые открытия и самое главное: найти интересное применение разнообразных приёмов разложения на множители к решению порой одинаковых по смыслу уравнений.

1. Что, значит, разложить многочлен на множители?

2. В каком случае произведение множителей равно 0?

3. Степень, какого числа равна нулю? 1??

4. Какие приёмы разложения на множители вам известны? (Вынесение общего множителя за скобки, группировка слагаемых с последующем вынесением общего множителя, с помощью формул сокращенного умножения).

5. Чему равны квадрат суммы, разности двух слагаемых?

6. Чему равна разность квадратов двух слагаемых?

На доске записаны уравнения:

По какому признаку можно разбить эти уравнения в группы? (Уравнения, содержащие многочлен второй степени. Уравнения, содержащие многочлен выше второй степени. Уравнение, содержащее многочлен второй степени, коэффициенты которого периодические дроби).

Нам предстоит решить эти уравнения, подбирая непохожие способы решения, несмотря порой на похожесть уравнений.

Предлагаю учащимся решить уравнение двумя способами. Вызываю к доске двух учеников.

Один ученик решает уравнение разбиением одночлена 6х на сумму двух одночленов, а другой – применением формулы сокращённого умножения – квадрата суммы:

Вопрос: Какой способ оказался более рациональным? (Конечно второй). Как его можно назвать?

(Выделение полного квадрата суммы)

Обсуждаем решение уравнения .

Можно ли решить уравнение, разбивая одно из слагаемых на два?

(да,)

А выделением полного квадрата суммы?

(затруднительно, так как, число 3 не является квадратом никакого рационального числа)

И всё-таки попробуем выделить полный квадрат суммы: дополните сумму первых двух слагаемых до квадрата суммы.

Как можно разложить многочлен в левой части уравнения на множители? (По формуле разности квадратов).

Сообразите, можно ли рассуждая аналогично решить уравнение ?

(Неудобное в данном случае число 5).

И все-таки, попробуем строго следовать формуле квадрата суммы при выделении полного квадрата:

Обратите внимание на коэффициенты уравнения . Какую закономерность можно заметить?

(Одинаково читаются слева направо)

Что происходит с показателями переменной x?

(Уменьшаются на один)

Выскажите предположение для многочлена в левой части уравнения.

(Многочлен х 4 +4х 3 +6х 2 +4х+1 есть (х+1) 4 ). Обоснуйте это.

(Построим треугольник Паскаля

14641 4-ая строка содержит коэффициенты возведения в 4-ую степень двучлена (х+1)

Итак, какой вид примет уравнение? Решите его устно.

Решите устно уравнение

Какими числами являются коэффициенты уравнения

(Периодическими десятичными дробями)

Обратите периодические дроби в обыкновенные и решите, получившееся уравнение.

(Правило обращения периодической десятичной дроби в обыкновенную: чтобы периодическую десятичную дробь обратить в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде и после девятки дописать столько нулей, сколько цифр между запятой и первым периодом)

(Подберите рациональный способ решения и найдите корни уравнения, х=1 или )

Вновь обратимся к уравнению . Решим это уравнение методом неопределённых коэффициентов:

Сравните значения найденных корней со значениями переменных b и d. (Они противоположны)

Найденные корни подтверждают мысль о том, что независимо от способа решения корни не меняются.

Чем уравнение похоже на предыдущее?

(Коэффициент при х 2 равен 1)

Попробуем решить это уравнение устно, не применяя ни один из рассмотренных приёмов, но

принимая во внимание некоторые рассуждения в предыдущем случае:

Запишите разложение многочлена в виде произведения двучленов:

Тогда, скажите чему, будут равны значения выражений и по аналогии с предыдущими рассуждениями?

( Легко догадаться, что или наоборот).

Сообразите, чему будут равны корни уравнения?

Устно решите уравнения:

1. С каким новым способом решения квадратных уравнений вы познакомились?

(Выделение полного квадрата суммы или разности)

2. Как вы думаете, почему этот способ не всегда удобен?

(Например, в уравнении 3х 2 -2х-1=0 3х 2 не является квадратом рационального выражения)

3. Какое открытие вы сделали, применяя метод неопределённых коэффициентов для

решения квадратных уравнений, если коэффициент при равен 1?

(Чтобы найти корни, надо сначала найти два таких числа в и с, чтобы их сумма была равна второму коэффициенту, а произведение – третьему слагаемому. А корни будут равны числам, противоположным числам .

В 8 классе вы познакомитесь с ещё одним способом решения квадратных уравнений – по формулам. Узнаете, кто такой Франсуа Виет и какое отношение он имеет к нашему открытию.

Видео:Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать

Урок алгебры в 7 классе Тема урока: Решение уравнений способами разложения многочлена на множители

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Рычкова Ирина Владимировна

МБОУ СОШ №23 г. Симферополь,

Республика Крым, Россия

Учитель высшей категории

Урок алгебры в 7 классе

Тема урока: Решение уравнений способами разложения многочлена на множители

систематизировать и обобщить изученные способы, попытаться сделать новые открытия;

найти интересное применение разнообразных способов разложения на множители к решению порой одинаковых по смыслу уравнений.

формирование алгоритмического мышления;

формирование у учащихся навыков умственного труда — планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов;

способствовать формированию умения обобщать изучаемые факты; продолжать учить чётко и ясно излагать свои мысли.

эстетическое воспитание учащихся;

формирование представлений о математике как части общечеловеческой культуры.

Методы обучения : проблемный, частично-поисковый.

I . Организационный момент.

II . Устная работа:

1. Какие способы разложения многочлена на множители вы знаете?

2.Решить уравнения: х 2 = 0; х 2 = 1; х 2 = -1; х 2 = 9; (х — 2) 2 = 0; (х + 4) 2 = 0;

х 2 – 49 = 0; х 2 + 49 = 0;

(х — 5)(х + 8) = 0; х(х + 4)(2х — 1) = 0.

II . Закрепление умений и навыков.

На доске записаны уравнения, содержащие многочлен второй степени:

Нам предстоит решить эти уравнения, подбирая непохожие способы решения, несмотря на схожесть этих уравнений.

1) Решить эти уравнения, применяя формулы сокращённого умножения – квадрата суммы и разности:

Этот способ решения – выделение полного квадрата суммы или разности.

2) Можно ли решить эти уравнения выделением полного квадрата суммы?

(затруднительно, так как, число 3 и 21 не являются квадратом никакого рационального числа)

И всё-таки попробуем выделить полный квадрат суммы: дополним сумму первых двух слагаемых до квадрата суммы:

3) Можно ли решить уравнение х 2 + 5х – 6 = 0 таким же способом? (затруднительно, так как, число 5 не раскладывается на множители с числом 2 и третье слагаемое имеет знак минус -6) И все-таки, попробуем строго следовать формуле квадрата суммы при выделении полного квадрата:

4) Вновь обратимся к уравнению х 2 + 6х + 9 = 0. Можно ли решить это уравнение без выделения полного квадрата суммы?

Решим это уравнение разбиением одночлена 6х на сумму двух одночленов 3х+3х:

Аналогично: (вызвать ученика)

5) Решим уравнение х 2 — 3х + 2 = 0 разбиением одночлена -3х на сумму двух одночленов (-2х –х) и число 2 на 1+1

:

6) Вновь обратимся к уравнению х 2 + 4х + 3 = 0. Решим это уравнение методом неопределённых коэффициентов:

Сравните значения найденных корней со значениями переменных b и d. (Они противоположны)

Найденные корни подтверждают мысль о том, что независимо от способа решения корни не меняются.

Чем уравнение х 2 — 5х + 6 = 0 похоже на предыдущее? (Коэффициент при х 2 равен 1)

Попробуем решить это уравнение принимая во внимание некоторые рассуждения в предыдущем случае:

Запишите разложение многочлена х 2 + 5х + 6 в виде произведения двучленов:

х 2 + 5х + 6 = (х + b )(х + c )

Тогда, b + c = 5 и b∙c = 6. Легко догадаться, что b = 2, c = 3 или наоборот. Значит корни уравнения будут равны х = -2 или х = -3.

b + c = 5; b = 2; x₁ = -2;

b ∙ c = 6; c = 3; x₂ = -3.

Вывод: метод неопределённых коэффициентов для решения уравнений, содержащие многочлен второй степени, если коэффициент при х 2 равен 1? (Чтобы найти корни, надо сначала найти два таких числа b и с, чтобы их сумма была равна второму коэффициенту, а произведение – третьему слагаемому. А корни будут равны числам, противоположным числам b и c.

Аналогично: х 2 — 7х + 10 = 0

b + c = -7; b = -2; x₁ = 2;

b ∙ c = 10; c = -5; x₂ = 5.

III. Подведение итогов

Вы познакомились с новыми способами решения уравнений, содержащие многочлен второй степени: выделение полного квадрата суммы или разности, разбиение одночлена на сумму двух одночленов, метод неопределённых коэффициентов.

В 8 классе вы познакомитесь с ещё одним способом решения квадратных уравнений – по формулам. Узнаете, кто такой Франсуа Виет и какое отношение он имеет к нашему открытию.

🎬 Видео

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Разложение на множители. 7 класс. Вебинар | МатематикаСкачать

Решение уравнений в 7 классе с помощью разложения многочленов на множители. Алгебра 7-11 класс.Скачать

7 класс, 30 урок, Разложение многочленов на множители с помощью формул сокращённого умноженияСкачать

Решение уравнений с помощью разложения на множители.(7 класс)Скачать

РЕШЕНИЕ УРАВНЕНИЯ С ПОМОЩЬЮ РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ. Примеры | АЛГЕБРА 7 классСкачать

Вынесение общего множителя за скобки | Алгебра 7 классСкачать

Разложение многочлена на множители способом группировки. Алгебра, 7 классСкачать

Применение различных способов для разложения на множители. Алгебра, 7 классСкачать

Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

7 класс, 29 урок, Способ группировкиСкачать

Решение уравнений с помощью разложения на множители.Скачать

7 класс// АЛГЕБРА // Применение различных способов для разложения на множителиСкачать

Разложение многочленов на множители.Метод #3.Метод группировки слагаемых.Скачать

Разложение на множители с помощью формул квадрата суммы и квадрата разности. Алгебра, 7 классСкачать

Алгебра 7. Урок 6 - Разложение на множители 1 - вынесение общего и группировкаСкачать

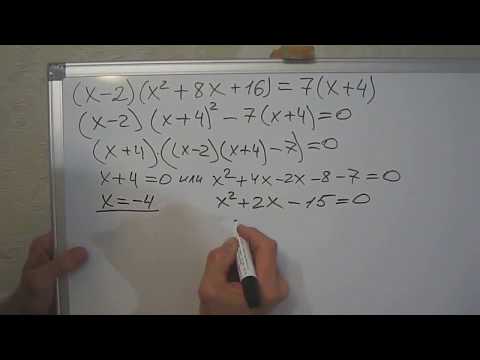
Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать

Алгебра 7. Урок 7 - Разложение на множители 2 - ФСУ и комбинированныйСкачать