§ 3. Решение систем с параметром и с модулями
В данном параграфе мы познакомимся со способами решения систем двух линейных уравнений с модулями.
Решите систему уравнений $$ left<beginleft|x-yright|=5,\ 3x+2y=10.endright.$$
Модуль в уравнении `|x-y|=5` можно «раскрыть», пользуясь определением модуля числа:
$$left|x-yright|=left<beginx-y,;mathrm;x-ygeq0,\y-x,;mathrm;x-y =0` записывается в виде `x-y=5`, а при `x-y =0`, система имеет вид:
Итак, `x=5`, `y=0`, условие `x-y>=0` выполняется. Значит, найденные пары чисел является решением исходной системы.
2 случай. Если `x-y =0`, `y>=0`;
4) `x =0`, `y>=0`, система имеет вид:
Оба полученные значения удовлетворяют заданным условиям: `1,5>=0`, `0>=0`.
2 случай. `x>=0`, `y =0`.
3 случай. `x =0` система имеет вид:
Первое уравнение не имеет решения, так как сводится к равенству `0=6`, значит система не имеет решений.
4 случай. `x -5/2`, то `|y+5/2|=y+5/2`; если `y то `|y+5/2|=-y-5/2`.
Выражение `y-1=0`, если `y=1`.
Если `y>1`, то `|y-1|=y-1`, а если `y =1`, то `|y-1|=y-1` и `|y+5/2|=y+5/2`, получаем уравнение:
Тогда `x=1/3(2*2+5)=3`. Число `2>1`, так что пара `(3;2)` является решением системы.
Пусть теперь `-5/2 хождения `y` получаем уравнение
Число `8/13` больше `(-5/2)`, но меньше, чем `1`, поэтому пара чисел `(27/13;8/13)` является решением системы.
Видео:✓ Параметр с модулями | ЕГЭ-2021. Задание 17. Математика. Профильный уровень | Борис ТрушинСкачать

Решение уравнений с модулями и параметрами
Презентация к уроку
Загрузить презентацию (434 кБ)
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные: научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие: развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные: воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a, если a > 0, число – a, если a <
Неравенство | x | 0) равносильно двойному неравенству – a 0.
Неравенство | x | > a, (если a > 0) равносильно двум неравенствам
Неравенство | x | > a, (если a : | x + 3 | + | y – 2 | = 4;
Расcмотрим четыре случая
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 < | x + 3 < | x 0 | y > – 2 |
| – x – 3 – y – 2 = 4 | y = x + 9 |
| < | x + 3 < | x 2 – 1) х = а + 1. Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи: 1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения 2) а = – 1; получаем ОX = О , и очевидно х – любое. Ответ: 3. Решения примеров (из вариантов С) 1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня. Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 | Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой
Числовая прямая при этом разбивает на 5 промежутков
Для случая 3) х0 = – b | 2a = 2, y0 = 25 : 2 + 25 – 10 = 2,5 Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10. Построим график функции, заданной равенством Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 2 – | x | = 6 1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10 1. Решить уравнение | x – 5 | – | 2x + 3| = 10 5. Итог урока 1. Определение модуля. 6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012 Видео:Как решать уравнение с параметром и модулем ★ Решите уравнение: x-|x|=aСкачать  Уравнения с параметром, содержащие модуль По свойству модуля при всех Учтем, что x ≥ 5, т.е. уравнение будет иметь уравнение будет иметь единственное решение на промежутке x ≥ 5. на промежутке x 1 уравнение имеет два корня При a 1, уравнение имеет два корня при a + 9 ≥ 0, т.е. a ≥ – 9 Учтем, что x ≥ – 3 Учтем, что x 9, неравенство имеет решение Т.е. при a > 0 a ≥ 0; т.е. 0 ≤ a ≤ 9; Т.е. при 0 ≤ a ≤ 9 уравнение имеет два различных корня. уравнение имеет два равных корня Ответим на поставленный вопрос. 2) y = – a – линейная функция, график прямая, параллельная оси OY.
Эскиз графиков. y
Найдем нули модуля: 2x + 6 = 0; x = –3; Раскроем модуль на двух промежутках: x ≥ –3 и x 3 /4 |
|
|
При 

Ответ: 


При каких значениях a уравнение 

 |
При каких значениях параметра a уравнение 
Так как 


Для того чтобы исходное уравнение имело два различных корня, новое уравнение должно иметь только один положительный корень. Это будет в двух следующих случаях:
а) один из корней положителен, другой отрицателен. Для этого достаточно, чтобы дискриминант был положительным, а произведение корней было отрицательным;
б) оба равных корня положительны. Для этого достаточно, чтобы дискриминант был равен нулю, а сумма корней была положительной.
Таким образом, получим совокупность двух систем.


Так как
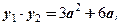






Откуда 
Ответ: 
При каких значениях с уравнение x 2 – ( 3c – 2 ) ∙ | x | + 2c 2 – c = 0 имеет 4 различных корня?
Для того чтобы исходное уравнение могло иметь четыре различных корня новое уравнение должно иметь два положительных корня. Это будет в том случае, когда дискриминант, произведение и сумма корней будут положительны.
Таким образом, получим систему неравенств:



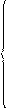
3c – 2 > 0; 
2c 2 – c > 0;
Ответ:
1. М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич. Сборник задач по алгебре 8-9.Москва, 2000
2. Г.А. Ястребинецкий. Задачи с параметрами. Москва, 1986
3. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992
4. В.В.Ткачук. Математика-абитуриенту,т1.Москва, 1994
5. С.Л.Попцов. Как решать задачи с параметром. Тверь, 1999
6. Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави, Москва, 2003
🔍 Видео
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

✓ Четыре способа решить параметр с модулем | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

Уравнения с модулемСкачать

✓ Параметр с тройным модулем | ЕГЭ. Задание 17. Математика. Профильный уровень | Борис ТрушинСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Уравнение с двойным модулем | Параметр 3 | mathus.ru |Скачать

Неравенства с модулем | Математика | TutorOnlineСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

Уравнение с двумя модулями: особенности решенияСкачать

Уравнения с параметром. Алгебра, 8 классСкачать

Уравнения с параметром. Алгебра 7 класс.Скачать

Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

#12. Крутое уравнение с параметром и модулем из ЕГЭ!Скачать

Сможешь решить уравнение с параметром? Что делать с модулем и при чем тут гипербола?Скачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Уравнение с двумя модулями - bezbotvyСкачать

Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

Уравнение с двумя модулями #1Скачать






 Решить в зависимости от значений параметра а.
Решить в зависимости от значений параметра а. левая часть уравнения неотрицательна, следовательно, при a 0 x – 3 = ± a, откуда x = 3 ± a.
левая часть уравнения неотрицательна, следовательно, при a 0 x – 3 = ± a, откуда x = 3 ± a. Учтем, что x 1. Т.е. при a > 1 Получим a > – 1. Т.е. при a > –1
Учтем, что x 1. Т.е. при a > 1 Получим a > – 1. Т.е. при a > –1 единственное решение
единственное решение 
 ;
;  ;
; . уравнение имеет два корня
. уравнение имеет два корня
 x ≥ – 3;
x ≥ – 3;  a ≥ – 9
a ≥ – 9
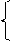 a ≤ 9; уравнение имеет один корень
a ≤ 9; уравнение имеет один корень
 .
.



 y = – a
y = – a