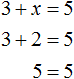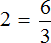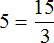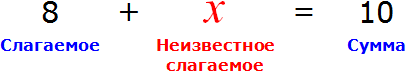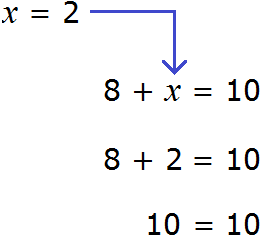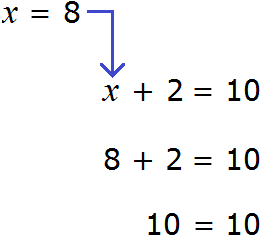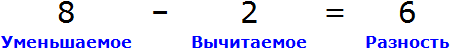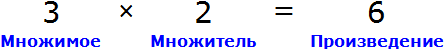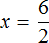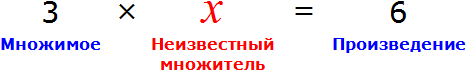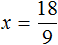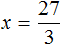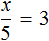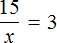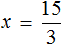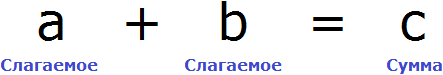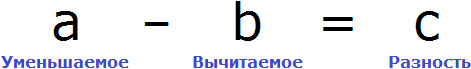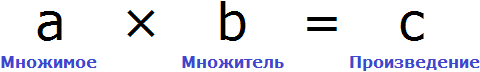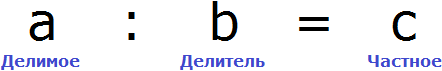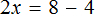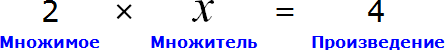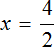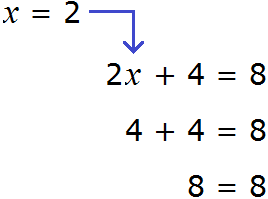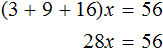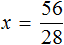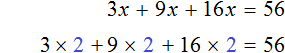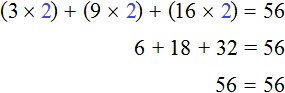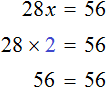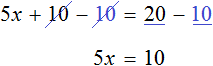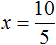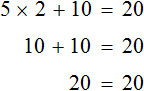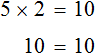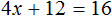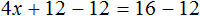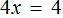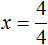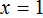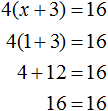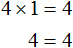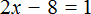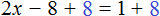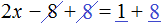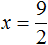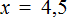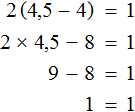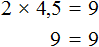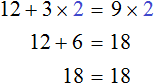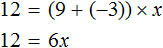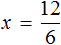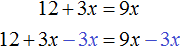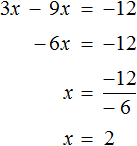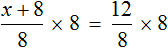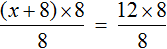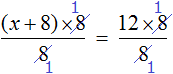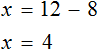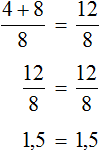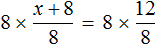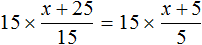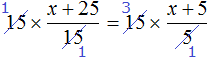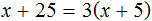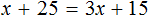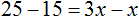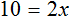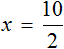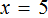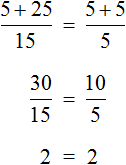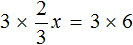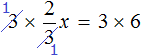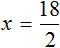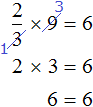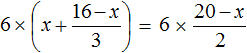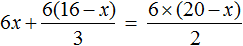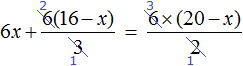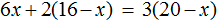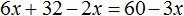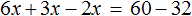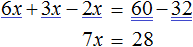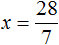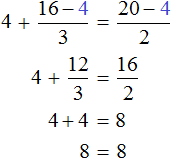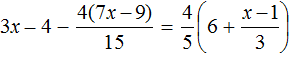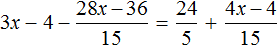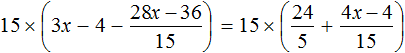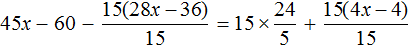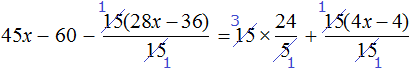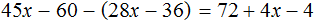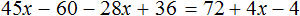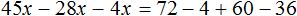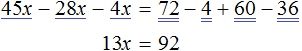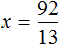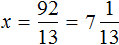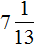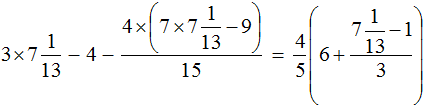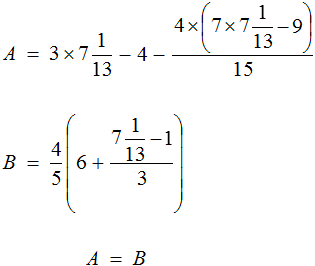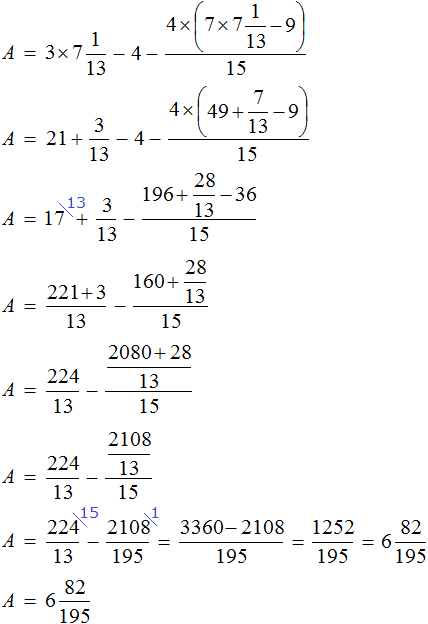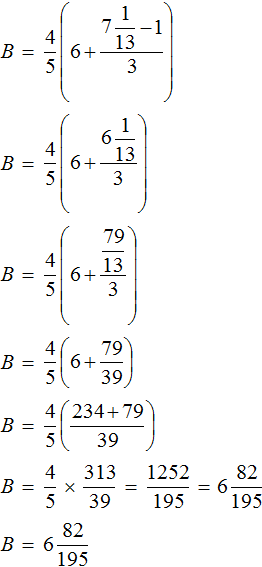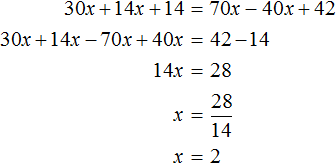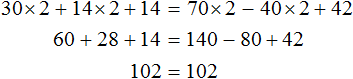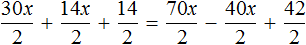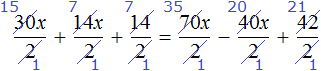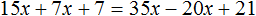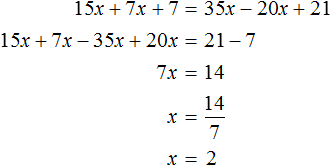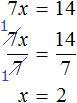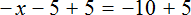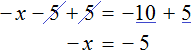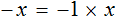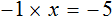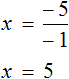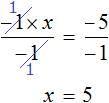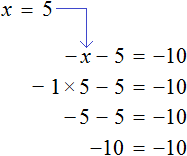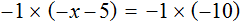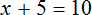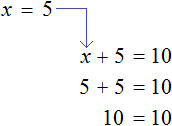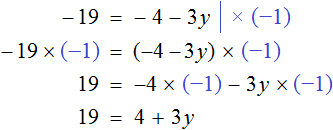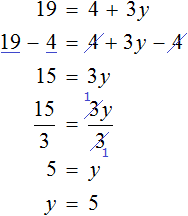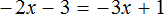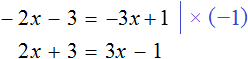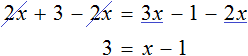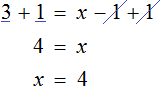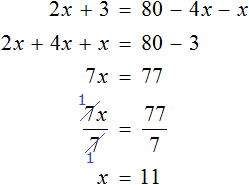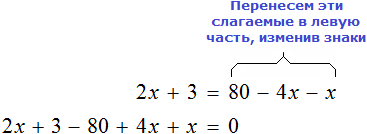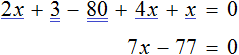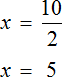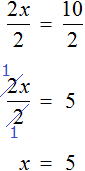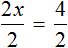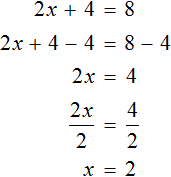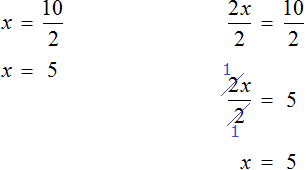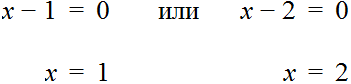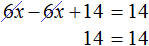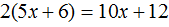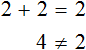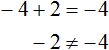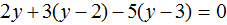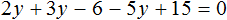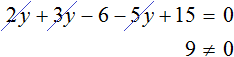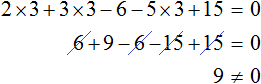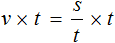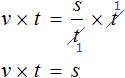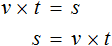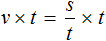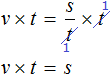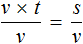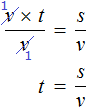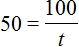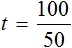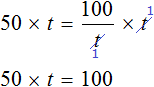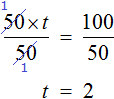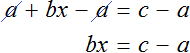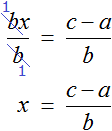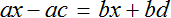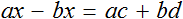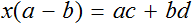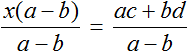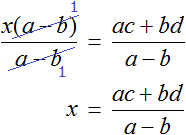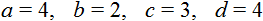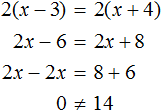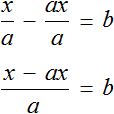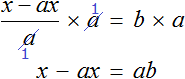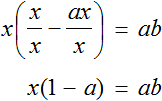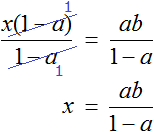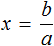Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
- Что такое уравнение?
- Выразить одно через другое
- Правила нахождения неизвестных
- Компоненты
- Равносильные уравнения
- Умножение на минус единицу
- Приравнивание к нулю
- Альтернатива правилам нахождения неизвестных
- Когда корней несколько
- Когда корней бесконечно много
- Когда корней нет
- Буквенные уравнения
- Линейные уравнения с одним неизвестным
- Презентация по математике на тему «Решение уравнений. Действия с положительными и отрицательными числами»
- Описание презентации по отдельным слайдам:
- Математика: теория и методика преподавания в образовательной организации
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Как решать уравнения с отрицательными числами и положительными числами
- Основные правила математики с примерами. 6 класс. Часть 2.
- Содержание
- 📸 Видео
Видео:Решение уравнений с отрицательными числами.Скачать

Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5 .
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x , значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение:
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
Мы выразили число 2 из равенства 8 + 2 = 10 . Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8 . Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2 есть разность числа 10 и числа 8
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно:
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство 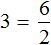
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
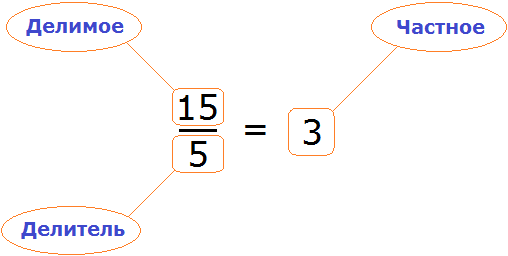
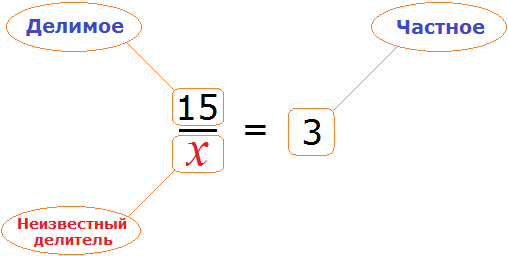
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Видео:Уравнения с отрицательными числами (Математика 6 класс)Скачать

Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10 , а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10 . Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10 . Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
А сейчас, чтобы найти неизвестное слагаемое x , мы должны из суммы 10 вычесть известное слагаемое 8:
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
Мы решили уравнение. Значение переменной x равно 2 . Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x , нужно из суммы 10 вычесть известное слагаемое 2
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6 . Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x , мы должны к разности 6 прибавить вычитаемое 2
Если вычислить правую часть, то можно узнать чему равна переменная x
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
Вычисляем правую часть и находим значение x
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6 . Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x , нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x .
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6 . Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства 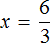
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда 
Решим уравнение x × 3 = 27 . Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда 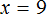
Вернемся к четвертому примеру из предыдущей темы, где в равенстве 
Чтобы выразить число 15 мы поступили следующим образом:
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства 
А сейчас, чтобы найти неизвестное делимое x , нужно частное 3 умножить на делитель 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
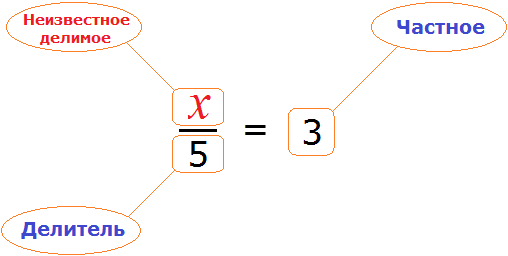
Теперь представим, что в равенстве 
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства 
А сейчас, чтобы найти неизвестный делитель x , нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x .
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Видео:как ЛЕГКО сложить отрицательные числа , ПРИМЕРЫСкачать
Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
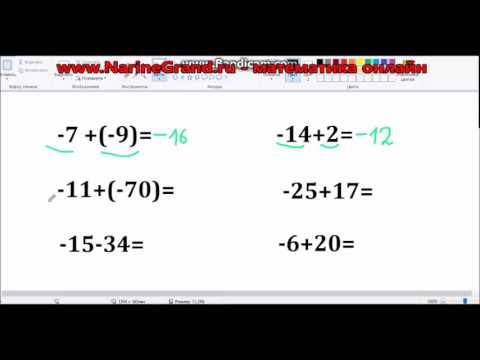
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вычислим правую часть, получим значение x равное 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x . После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение 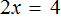
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение 
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Видео:Как вычитать отрицательные числа? / Простые примеры из жизни по математикеСкачать

Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56 , мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56 . Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2 . Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56 , а затем в уравнение 28x = 56 , которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56 , которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 10 разделить на известный сомножитель 5.
Отсюда 
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
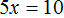

Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
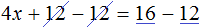
Получили уравнение 4x = 4 . Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x , нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12 . В результате получили равносильное уравнение 4x = 4 . Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x , а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению 
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 
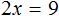

Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения 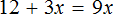
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
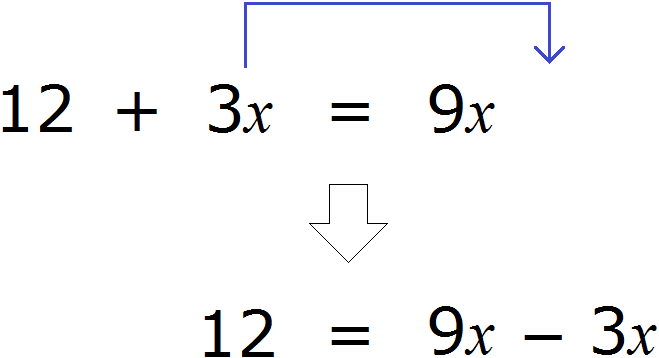
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x . Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда x = 2 . Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12 . В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению 
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение 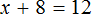

Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение 
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения 
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению 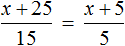
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15 . Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x . Корень этого уравнения, как и уравнения 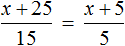
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение 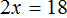
Отсюда
Вернемся к исходному уравнению 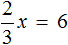
Получается верное числовое равенство. Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x , сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x . Для этого разделим произведение 28 на известный сомножитель 7
Вернемся к исходному уравнению 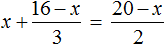
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A , а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно 

Видим, что значение переменной B , как и значение переменной A равно 
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42 . Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2 . Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14 , нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Видео:№ 6. Действия с положительными и отрицательными числами (6 класс)Скачать

Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1 .
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение 
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения 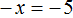
То есть минус, стоящий перед переменной x, относится не к самой переменной x , а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение 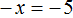
Имеем дело с компонентами умножения. Чтобы найти х , нужно произведение −5 разделить на известный сомножитель −1 .
или разделить обе части уравнения на −1 , что еще проще
Итак, корень уравнения 
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения 
После раскрытия скобок в левой части образуется выражение 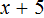
Корень этого уравнения, как и уравнения 
Значит уравнения 
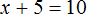
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение 
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения 
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения 
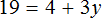
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1 . Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Видео:Сложение и вычитание рациональных и отрицательных рациональных чисел. Практическая часть. 6 класс.Скачать
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение 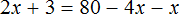
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77 , и разделим обе части на 7
Видео:Все действия с отрицательными числами за 2 минутыСкачать

Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении 
Но если в уравнении 
Уравнения вида 
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении 
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда 
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида 
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Видео:Положительные и отрицательные числа. 6 класс.Скачать

Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9 .
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9) , которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0 . Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0 . Несложно догадаться, что корень этого уравнения равен −9 . Проверка показывает, что корень верный:
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2) . А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2) ).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение 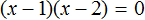
Видео:6 класс, 33 урок, Сложение чисел с разными знакамиСкачать

Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14 . Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Видео:Решение уравнений, 6 классСкачать

Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение 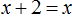
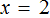
Пусть
Пример 2. Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y . Например, пусть y = 3 .
Видео:Умножение рациональных чисел. 6 класс.Скачать

Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения 
Умнóжим обе части уравнения 
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения 
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
А расстояние равно 100 км
Тогда буквенное уравнение 
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t . Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение 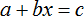
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10 . Оно похоже на буквенное уравнение a + bx = c . Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0) , поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение 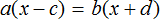
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x , сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b . Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d) , то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4) . Оно похоже на уравнение a(x − c) = b(x + d) . Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d . Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0) . Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d) . В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение 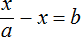
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Видео:Математика 6 класс (Урок№35 - Отрицательные дроби.)Скачать

Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2 (x + 3) = 16 . Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2 x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2 x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x , разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2 (x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10 , для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x . Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0 , то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0 . При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0 , то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5 . Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0 , и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3 , и b равно какому-нибудь числу, скажем числу 6 , то уравнение 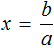
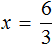
Отсюда 
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0 . Это то же самое уравнение, что и ax = b , но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0 . Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
Видео:Сложение и вычитание отрицательных чисел.Скачать

Презентация по математике на тему «Решение уравнений. Действия с положительными и отрицательными числами»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Описание презентации по отдельным слайдам:
Сказка
«Магическая сила
корня уравнения»
Смирнова Лариса Валентиновна
МБОУ «СШ № 1» г. Иваново
В мире много сказок
Грустных и смешных.
И прожить на свете
Нам нельзя без них!
Пусть герои сказок
Дарят нам тепло,
пусть добро навеки
побеждает зло!
В некотором царстве,
в некотором государстве
жил-был Иван –царевич.
Повстречал как-то
Иван-царевич Елену Прекрасную.
Полюбили они друг друга.
Но злой Кощей Бессмертный похитил Елену Прекрасную
И поехал Иван-царевич искать свою Елену-Прекрасную. Едет он по дороге, а на пути лежит камень.
На камне написано три уравнения
Если правильно решить уравнения, то Иван найдет нужное направление
(х -2,7) + 3,6 = 7,2
(Х + 3,5) – 2,4 = — 10
(2,9 + х) – 3,9 = — 1
Если х 0, то пропадешь
в дремучем лесу;
Если х = 0, то ехать нужно прямо.
Долго ехал Иван -царевич
по дороге и дорога привела его к избушке Бабы Яги.
Она давно враждовала с Кощеем Бессмертным.
Баба Яга: «Помогу тебе
Иван — царевич, только
при условии,
если ты решишь уравнения, написанные на стене избушки и найдешь нужный корень уравнения.»
2) 2х + 5х – 3,4 = — 0,6
3) ( 5х – 18,9) : 3 = — 6,3
Х-натуральное число
(Иван останется у Бабы Яги)
Х – дробное число
(Иван ищет дорогу самостоятельно)
Х = 0 (Баба Яга помогает Ивану)
Прощаясь с Иваном,
Баба Яга рассказала ему секрет:
«Если нужно тебе открыть какой-либо замок, произнеси вслух корни уравнения,
только назови их в порядке возрастания. И мигом все замки откроются.»
Поблагодарил
Иван Бабу Ягу и
поехал дальше.
Долго ехал – коротко ли, стемнело и попал Иван Царевич в западню. Слуги Кощея Бессмертного схватили его и заперли в подземелье
Вспомнил Иван слова
Бабы Яги и произнес
«волшебные слова»
Двери подземелья
открылись
Подъехал Иван к воротам царства, а на воротах уравнение
(х + 5,12) – 5,12 = 1
Иван — царевич быстро решил уравнение,
ворота открылись. Освободил он свою
Елену Прекрасную.
Сыграли они свадьбу и жили долго и счастливо.
Математика всегда приходит на помощь
!
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 696 человек из 76 регионов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 858 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 46 человек из 20 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:Действия с положительными и отрицательными числамиСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 843 605 материалов в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 05.04.2017
- 171
- 0
- 05.04.2017
- 199
- 2
- 05.04.2017
- 229
- 0
- 05.04.2017
- 230
- 0
- 05.04.2017
- 172
- 0
- 05.04.2017
- 221
- 0
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 05.04.2017 316
- PPTX 4.6 мбайт
- 10 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Смирнова Лариса Валентиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 110902
- Всего материалов: 62
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Модуль числа. Практическая часть. 6 класс.Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Инфофорум о буллинге в школе: итоги и ключевые идеи
Время чтения: 6 минут
В Госдуме предложили унифицировать школьные программы
Время чтения: 1 минута
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Деление рациональных чисел. 6 класс.Скачать
Как решать уравнения с отрицательными числами и положительными числами
Математику уж затем учить надо, что она ум в порядок приводит
Основные правила математики с примерами. 6 класс. Часть 2.
Содержание
Умножение. Свойства умножения
Произведением числа на натуральное число
не равное 1, называют сумму, состоящую из
слагаемых, каждое из которых равно а:
a · b = a + a + a + . . . + a ⏟ b
Если один из двух множителей равен 1, то произведение равно второму множителю:
Если один из множителей равен нулю, то произведение равно нулю:
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
!Важное правило. Помогает решать уравнения
( x — a ) ( x — b ) = 0 ; И л и x — a = 0 , и л и x — b = 0 ; 2 к о р н я x = a и x = b . ( x — 5 ) ( x + 2 ) = 0 ; И л и x — 5 = 0 , и л и x + 2 = 0 ; 2 к о р н я x = 5 и x = — 2 .
Умножение обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Умножение рациональных чисел
Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
Чтобы умножить два отрицательных числа, надо умножить их модули.
Для любого рационального числа :
Если произведение •
— отрицательное, то числа
и
имеют разные знаки.
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
a b : c d = a b · d c
Деление рациональных чисел
Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
Нахождение дроби от числа
Чтобы найти дробь от числа, можно число умножить на эту дробь.
Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
Нахождение числа по его дроби
Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.
Найти число, если известно, что
е г о д р о б ь 5 7 с о с т а в л я е т ч и с л о 15 : 15 : 5 7 = 15 · 7 5 = 15 3 · 7 5 1 = 21
Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
Найти число, если известно, что
24 % э т о г о ч и с л а р а в н ы 48 . 24 % = 24 100 ; 48 : 24 100 = 48 · 100 24 = 48 2 · 100 24 1 = 200
Степень числа
Степенью числа с натуральным показателем
, большим
, называют произведение
множителей, каждый из которых равен
:
a n = a · a · a · … · a ⏟ n
Число при этом называют основанием степени.
Степенью числа с показателем
называют само число
Вторую степень числа называют также квадратом числа. Например, запись читают: «
в квадрате».
Третью степень называют кубом числа, а запись читают: «
в кубе».
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.
Найти значение выражения
5 · 2 3 + 15 5 · 2 2 3 1 + 3 15 = 5 · 8 + 15 = 40 + 15 = 55
Числовые и буквенные выражения
Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.
Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
Приведение подобных слагаемых
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
Раскрытие скобок
Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
Отношения
- Частное двух чисел
и
, не равных нулю, еще называют отношением чисел
и
, или отношением числа
к числу
.
- Отношение положительных чисел
и
показывает, во сколько раз число
больше числа
, или какую часть число
составляет число
.
показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Пропорции
Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
a : b = c : d и л и a b = c d
Числа и
называют крайними членами пропорции, а числа
и
— средними членами пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
a b = c d ⇒ a d = b c
Если ,
,
и
числа, не равные нулю, и
•
=
•
, то отношения
могут образовывать пропорцию
Процентное отношение двух чисел
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Прямая и обратная пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если величины и
обратно пропорциональны, то их соответствующие значения удовлетворяют равенству
, где -число, постоянное для данных величин.
📸 Видео
Математика 6 Умножение и деление положительных и отрицательных чиселСкачать

Действия с положительными и отрицательными числамиСкачать

Умножение и деление чисел с разными знаками (положительных и отрицательных чисел)Скачать