- Определение
- График натурального логарифма ln x
- Свойства натурального логарифма
- Область определения, множество значений, экстремумы, возрастание, убывание
- Значения ln x
- Основные формулы натуральных логарифмов
- Основное свойство логарифмов и его следствия
- Формула замены основания
- Обратная функция
- Производная ln x
- Интеграл
- Выражения через комплексные числа
- Разложение в степенной ряд
- Как решать логарифмические уравнения подробный разбор примеров
- Сложение и вычитание логарифмов.
- Что такое логарифм и как его посчитать
- Два очевидных следствия определения логарифма
- Свойства логарифмов
- Степень можно выносить за знак логарифма
- Логарифм произведения и логарифм частного
- Формула перехода к новому основанию
- Сумма логарифмов. Разница логарифмов
- Логарифмический ноль и логарифмическая единица
- Как решать уравнения с логарифмами: 2 способа с примерами
- Сравнение логарифмов
- Пример Найдите корень уравнения.
- Логарифмы со специальным обозначением
- Десятичный логарифм
- Натуральный логарифм
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Использование свойств логарифмов при решении логарифмических уравнений и неравенств
- Логарифмическое уравнение: решение на примерах
- Как решать уравнения с логарифмами: 2 способа с примерами
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Как сделать проверку
Видео:Производная логарифмической функции. 11 класс.Скачать

Определение
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x )′ = 1/ x .
Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045. ;
.
Видео:Решение логарифмических уравнений #shortsСкачать

График натурального логарифма ln x
График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .
Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.
При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).
При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
| Область определения | 0 |
| Область значений | – ∞ |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет |
| + ∞ | |
| – ∞ |
Значения ln x
Видео:Десятичные и натуральные логарифмы. Видеоурок 16. Алгебра 10 классСкачать

Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм».
Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Обратная функция
Обратной для натурального логарифма является экспонента.
Если 0)» style=»width:132px;height:20px;vertical-align:-11px;background-position:-296px -320px»> , то
Видео:Десятичный логарифмСкачать
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >
Видео:Производная 5 Экспонента и натуральный логарифм.Скачать

Интеграл
Видео:Как решать логарифмы? Что такое ln и lg #егэпрофиль #профиль #егэ #умскул #аделияадамова #умскулегэСкачать
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z :
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n .
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Видео:Что такое Логарифмы? для ЧайниковСкачать

Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 05-04-2014 Изменено: 20-03-2017
Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Как решать логарифмические уравнения подробный разбор примеров
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Сложение и вычитание логарифмов.
Возьмем два логарифма с одинаковыми основаниями: loga x и loga y. Тогда сними возможно выполнять операции сложения и вычитания:
Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов – логарифму частного. Причем это верно если числа а, х и у положительны и а ≠ 1.
Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!
Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.
Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а, x и у положительны и а ≠ 1, то:
Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а, х и у положительны и а ≠ 1, то:
Применим вышеизложенные теоремы для решения примеров:
Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:
так как выражения log2(-8) и log2(-4) вообще не определены (логарифмическая функция у = log2х определена лишь для положительных значений аргументах).
Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x1, x2, . . . ,xn существует тождество :
Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что loga1= 0, следовательно,
А значит имеет место равенство:
Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:
Видео:Натуральные логарифмы. Функция у=ln х | Алгебра 11 класс #17 | ИнфоурокСкачать

Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:

b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X. 

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Два очевидных следствия определения логарифма
log a 1 = 0 ( a > 0, a ≠ 1 )
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.
Видео:Производная от lnx - Профильная Математика ЕГЭСкачать

Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
 |  | ||||||||||||||
 |  | ||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | ( формула перехода к новому основанию логарифмов ), | ||||||||||||||
 | |||||||||||||||
 |
Видео:Логарифмы с нуля за 30 минут. Логарифмы 10 класс ЕГЭ профиль математика | УмскулСкачать  Степень можно выносить за знак логарифмаИ вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример: log a ( f ( x ) 2 = 2 log a f ( x ) Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени. Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать  Логарифм произведения и логарифм частногоlog a b c = log a b − log a c ( a > 0, a ≠ 1, b > 0, c > 0 ) Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании “слева направо” происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного – расширение ОДЗ. log a ( f ( x ) g ( x ) ) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля. Преобразуя данное выражение в сумму log a f ( x ) + log a g ( x ) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6). Видео:Логарифмы в ЕГЭ⚡️что получилось?!Скачать  Формула перехода к новому основаниюТот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной. Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8): log a b = 1 log b a ( a > 0, a ≠ 1, b > 0, b ≠ 1 ) Видео:Как решать уравнения с дробью? #shortsСкачать  Сумма логарифмов. Разница логарифмовЛогарифмы с одинаковыми основаниями можно складывать: Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя! Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать  Логарифмический ноль и логарифмическая единицаЭто следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор. Запомните, что логарифм от a по основанию а всегда равен единице: loga a = 1 – это логарифмическая единица. Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1: loga 1 = 0 – логарифмический ноль. Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать  Как решать уравнения с логарифмами: 2 способа с примерамиРешить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида: При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку! Давайте посмотрим, как это работает на примере: Воспользуемся определением логарифма и получим: Теперь перед нами простейшее уравнение, решить которое не составит труда: Сделаем проверку. Подставим найденный Х в исходное уравнение: Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ. Поэтому мы покажем еще один способ решения логарифмических уравнений. Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так: Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере. Решим еще раз то же самое уравнение, но теперь этим способом: Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его: Воспользуемся этим свойством в нашем случае, получим: Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений. Разберем другой пример: Теперь делаем проверку: Еще один пример решения логарифмического уравнения:
Теперь подставим х2 = -5 в исходное уравнение: Сравнение логарифмов
| ||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
|
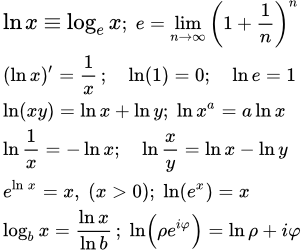

























 Логарифмы с одинаковыми основаниями можно вычитать:
Логарифмы с одинаковыми основаниями можно вычитать: 
 Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
 Вспоминаем определение логарифма и получаем следующее:
Вспоминаем определение логарифма и получаем следующее:  Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
 Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
 В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2. То есть в нашем случае:
То есть в нашем случае:  То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать:
То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать: Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
 Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:
Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили: Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение: Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:  Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:  Теперь можно зачеркнуть логарифмы и тогда получим:
Теперь можно зачеркнуть логарифмы и тогда получим:  Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней:
Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней: то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
то последнее выражение верно. Следовательно, х = 3 является корнем уравнения. Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:  Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:  Выполнив преобразования правой и левой частей уравнения, мы получили:
Выполнив преобразования правой и левой частей уравнения, мы получили:  Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы:
Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы: Решим данное квадратное уравнение, найдем дискриминант:
Решим данное квадратное уравнение, найдем дискриминант: Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:  Верно, следовательно, х1 = 1 является корнем уравнения.
Верно, следовательно, х1 = 1 является корнем уравнения. Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.








 Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.



 Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
 Применяем эти знания и получаем:
Применяем эти знания и получаем:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:  Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма: Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:
Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:  Делаем проверку:
Делаем проверку:  Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:
Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим: Верно, следовательно, х = 4 является корнем уравнения.
Верно, следовательно, х = 4 является корнем уравнения. Преобразуем правую часть уравнения:
Преобразуем правую часть уравнения:  Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:
Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:  Теперь мы можем зачеркнуть логарифмы:
Теперь мы можем зачеркнуть логарифмы:  Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:


 Перепишем нашу систему:
Перепишем нашу систему:  Перепишем нашу систему: Следовательно, наша система примет следующий вид:
Перепишем нашу систему: Следовательно, наша система примет следующий вид:  Теперь решаем наше уравнение:
Теперь решаем наше уравнение:  Теперь решаем наше уравнение: Справа у нас квадрат суммы:
Теперь решаем наше уравнение: Справа у нас квадрат суммы: Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.

 Вспоминаем определение логарифма и получаем следующее:
Вспоминаем определение логарифма и получаем следующее: Таким образом мы получаем простое уравнение, которое сможем легко решить.
Таким образом мы получаем простое уравнение, которое сможем легко решить.
 Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
 В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2. То есть в нашем случае:
То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать:
Возьмем правую часть нашего уравнения и начнем ее преобразовывать: Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
 Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:
Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили: Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение: Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:
Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:
После преобразования правой части наше уравнение принимает следующий вид: Теперь можно зачеркнуть логарифмы и тогда получим:
Теперь можно зачеркнуть логарифмы и тогда получим: Вспоминаем свойства степеней:
Вспоминаем свойства степеней: то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
то последнее выражение верно. Следовательно, х = 3 является корнем уравнения. Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:
Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:
Теперь преобразуем правую часть уравнения: Выполнив преобразования правой и левой частей уравнения, мы получили:
Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем зачеркнуть логарифмы:
Теперь мы можем зачеркнуть логарифмы: Решим данное квадратное уравнение, найдем дискриминант:
Решим данное квадратное уравнение, найдем дискриминант: Сделаем проверку, подставим х1 = 1 в исходное уравнение:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:
 Верно, следовательно, х1 = 1 является корнем уравнения.
Верно, следовательно, х1 = 1 является корнем уравнения. Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень. Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
 Применяем эти знания и получаем:
Применяем эти знания и получаем: Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
 Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:
Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть: Делаем проверку:
Делаем проверку: Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:
Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим: Верно, следовательно, х = 4 является корнем уравнения.
Верно, следовательно, х = 4 является корнем уравнения. Преобразуем правую часть уравнения:
Преобразуем правую часть уравнения: Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:
Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части: Теперь мы можем зачеркнуть логарифмы:
Теперь мы можем зачеркнуть логарифмы: Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:


 Перепишем нашу систему:
Перепишем нашу систему: Следовательно, наша система примет следующий вид:
Следовательно, наша система примет следующий вид: Теперь решаем наше уравнение:
Теперь решаем наше уравнение: Справа у нас квадрат суммы:
Справа у нас квадрат суммы: Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
