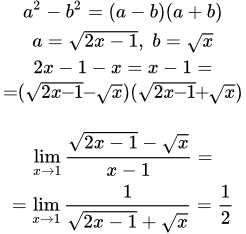Как решать уравнения с лимитами с корнями (4 видео)

Решение пределов с корнями

Содержание

Методы решений
Примеры решений
Решение подстановкой
Пример 1
Пример 2
Неопределенность ∞ / ∞
Пример 3
Линеаризация бесконечно малых (больших) функций
Пример 4
Пример 5
Пример 6
Как решать уравнения с лимитами с корнями
Пределы с иррациональностями. Первая часть.
Раскрытие неопределенности $frac$.
🔍 Видео

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Методы решений

Для вычисления пределов с корнями, применяются приемы и методы, аналогичные методам вычисления пределов с многочленами (см. «Раскрытие неопределенностей с дробями», «Решение пределов с дробями из многочленов»). При этом возможны следующие дополнительные приемы, специфичные для функций с корнями.
1) Убрать корни с помощью подстановки, применяя теорему о пределе сложной функции. Примеры ⇓
2) Разделить числитель и знаменатель на x s (в случае неопределенности вида ∞/∞ при x → ∞ ), где s – некоторое подобранное число. Пример ⇓
3) Выразить бесконечно малые функции, содержащие корни, через бесконечно малые линейные функции, используя приведенные ниже формулы (то же самое в случае разности бесконечно больших функций). Примеры ⇓
4) Иногда удобно бесконечно малую функцию преобразовать в сумму или разность бесконечно малых функций, пределы от которых легко находятся. Пример ⇓

В последних двух случаях применяются следующие формулы:
;
;
;
. . . . . . . .
.
Например:
;
;
.

Эти же формулы применяют и для раскрытия разности бесконечно больших функций: .

Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Примеры решений

Все примеры Далее мы приводим подробные решения следующих примеров.
Найти предел последовательности:
решение ⇓
Найти следующие пределы функций с корнями:
⇓ , ⇓ , ⇓ , ⇓ , ⇓ .

Решение подстановкой

Пример 1

Подставим . Тогда .
При .
Мы имеем неопределенность вида .

Замечаем, что от корня можно освободится, если сделать подстановку .
Тогда функцию за знаком предела можно представить как сложную:
,
где , .
Тогда нам нужно найти предел сложной функции
, где .

Применим теорему о пределе сложной функции. Но поскольку функция строго монотонна, то мы применим ее разновидность – теорему о пределе функции от монотонной функции.

Для этого сначала вычисляем предел . Поскольку функция непрерывна на всей области определения, то этот предел равен значению функции в точке :
.

Теперь вычисляем второй предел:
.
Он не содержит корней. То есть мы свели задачу к пределу от разности дробей многочленов. Применяем методы, изложенные на странице «Решение пределов с дробями из многочленов».

Разложим знаменатель на множители и приводим дроби к общему знаменателю:
;

.
Делим числитель и знаменатель на . При имеем:
.
Находим предел:
.

По теореме о пределе функции от монотонной функции,
.

Пример 2

Все примеры ⇑ Найти предел последовательности:
.

Преобразуем элемент заданной последовательности, воспользовавшись свойствами корней:
.

Если мы найдем предел функции
,
то согласно определению предела функции по Гейне, искомый предел заданной последовательности будет равняться этому пределу: , поскольку при .

Находим предел отношения многочленов, выделяя и сокращая в числителе и знаменателе множитель :

Неопределенность ∞ / ∞

Пример 3

Все примеры ⇑ Найти предел отношения корней:
.

Здесь, при числитель и знаменатель стремятся к . У нас неопределенность вида . Для ее раскрытия, последовательно выносим бесконечно большую часть в числителе и знаменателе за скобки. При имеем:
;

;
;

;
.

Линеаризация бесконечно малых (больших) функций

Пример 4

Все примеры ⇑ Найти предел дроби с корнями:
.

Подставим в числитель и знаменатель:
;
.
Числитель и знаменатель обращаются в нуль. Мы имеем неопределенность вида 0/0 .
Для ее раскрытия, линеаризуем бесконечно малые функции, используя формулу:
(П4.1) .

Делим числитель и знаменатель на и находим предел:

.
Здесь , .

Пример 5

Подставим в числитель и знаменатель:
;
.
Мы имеем неопределенность вида 0/0 .

Чтобы упростить вычисления, здесь удобно представить бесконечно малые функции в числителе и знаменателе в виде сумм и разностей других бесконечно малых функций:
(П5.1) .

Применим формулу:
.
Подставим :
.
Отсюда
, где .
Заметим, что .

Применим формулу:
.
Подставим :

.
Отсюда
, где .
.

Наконец, применим формулу:
.
Подставим :

.
Отсюда
, где .
.

Подставляем полученные выражения в (П5.1):
.
Делим числитель и знаменатель на x . В результате мы освобождаемся от неопределенности и находим предел непрерывной функции:

Можно было записать и так:

.
После чего вычислить пределы:
.

Пример 6

Все примеры ⇑ Найти предел функции с корнями при x стремящемся к бесконечности:
.

Поскольку, при , и , то мы имеем неопределенность вида +∞ – (+∞) .

Применим формулу:
(П6.1) .
Подставим :

.
Отсюда, при имеем:
(П6.2) .

В числителе опять неопределенность +∞ – (+∞) . Применяем формулу (П6.1) еще раз. Подставим :

.
Отсюда
.

Подставим в (П6.2):
,
где .
Теперь у нас неопределенность вида ∞/∞ . Для раскрытия этой неопределенности, преобразуем знаменатель. Выделим бесконечно большую часть и вынесем ее за скобки. При имеем:
;

;
;

;
;
.

Делим числитель и знаменатель в функции на . При имеем:
.
Находим предел.
При , ,

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин. Сборник задач по высшей математики. Том 1. Москва, 1957.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Б.П. Демидович. Сборник задач и упражнений по математическому анализу. Москва, 1997.

Автор: Олег Одинцов . Опубликовано: 02-02-2019 Изменено: 30-11-2021

Видео:29. Вычисление пределов функции №4. Неопределенность 0/0 с корнями.Скачать

Как решать уравнения с лимитами с корнями

К примеру, если вы хотите ввести разность двух корней, то укажите следующее выражение:

sqrt(x^2 + 2*x) — sqrt(-3 + x^2)

Для этого примера вы получите подробное решение:

Для случая, когда корень находится в числителе или знаменателе дроби, то, к примеру, введите так:

(sqrt(x + 1) — sqrt(2*x — 2))/(x — 3)

Не забудьте указать к чему стремится переменная x.

Для указанного примера Вы также получите подробное решение, но с применением правила Лопиталя.

Ещё раз приводим ссылку на калькулятор:

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Пределы с иррациональностями. Первая часть.

Пределы, содержащие иррациональности (или, попросту говоря, корни) крайне популярны у составителей типовых расчётов и контрольных работ по высшей математике. Обычно рассматриваются три группы неопределённостей:

Неопределённость вида $frac$. Пример: $lim_frac<sqrt-2><4-sqrt>$.
Неопределенность вида $frac$. Пример: $lim_frac<9cdot sqrt[3]+7cdotsqrt[4]><11cdot sqrt[6]+4x-10>$.
Неопределенность вида $infty-infty$. Пример: $lim_left( sqrt-sqrt right)$.

В данной теме мы рассмотрим все три перечисленные выше группы пределов с иррациональностями. Начнём с пределов, содержащих неопределенность вида $frac$.

Видео:Предел функции на бесконечности. 10 класс.Скачать

Раскрытие неопределенности $frac$.

Схема решения стандартных примеров такого типа обычно состоит из двух шагов:

Избавляемся от иррациональности, вызвавшей неопределенность, домножая на так называемое «сопряжённое» выражение;
При необходимости раскладываем выражение в числителе или знаменателе (или и там и там) на множители;
Сокращаем множители, приводящие к неопределённости, и вычисляем искомое значение предела.

Термин «сопряжённое выражение», использованный выше, будет детально пояснён в примерах. Пока что останавливаться на нём подробно нет резона. Вообще, можно пойти иным путём, без использования сопряжённого выражения. Иногда от иррациональности может избавить удачно подобранная замена. Такие примеры редки в стандартных контрольных работах, поэтому на использование замены рассмотрим лишь один пример №6 (см. вторую часть данной темы).

Нам понадобится несколько формул, которые я запишу ниже:

Кроме того, предполагаем, что читатель знает формулы для решения квадратных уравнений. Если $x_1$ и $x_2$ – корни квадратного трёхчлена $ax^2+bx+c$, то разложить его на множители можно по следующей формуле:

Формул (1)-(5) вполне хватит для решения стандартных задач, к которым мы сейчас и перейдём.

Найдём отдельно пределы числителя и знаменателя:

В заданном пределе мы имеем неопределённость вида $frac$. Раскрыть эту неопределённость нам мешает разность $sqrt-2$. Для того, чтобы избавляться от подобных иррациональностей, применяют умножение на так называемое «сопряжённое выражение». Как действует такое умножение мы сейчас и рассмотрим. Умножим $sqrt-2$ на $sqrt+2$:

Чтобы раскрыть скобки применим формулу №1, подставив в правую часть упомянутой формулы $a=sqrt$, $b=2$:

Как видите, если умножить числитель на $sqrt+2$, то корень (т.е. иррациональность) в числителе исчезнет. Вот это выражение $sqrt+2$ и будет сопряжённым к выражению $sqrt-2$. Однако мы не вправе просто взять и умножить числитель на $sqrt+2$, ибо это изменит дробь $frac<sqrt-2>$, стоящую под пределом. Умножать нужно одовременно и числитель и знаменатель:

Теперь вспомним, что $(sqrt-2)(sqrt+2)=3-x$ и раскроем скобки. А после раскрытия скобок и небольшого преобразования $3-x=-(x-3)$ сократим дробь на $x-3$:

Неопределенность $frac$ исчезла. Сейчас можно легко получить ответ данного примера:

Замечу, что сопряжённое выражение может менять свою структуру – в зависимости от того, какую именно иррациональность оно должно убрать. В примерах №4 и №5 (см. вторую часть данной темы) будет использован иной вид сопряжённого выражения.

Запишем пределы числителя и знаменателя:

Мы имеем дело с неопределённостью вида $frac$. Избавимся от иррациональности в знаменателе данной дроби. Для этого доможим и числитель и знаменатель дроби $frac<sqrt-sqrt>$ на выражение $sqrt+sqrt$, сопряжённое к знаменателю:

Вновь, как и в примере №1, нужно использовать формулу №1 для раскрытия скобок. Подставив в правую часть упомянутой формулы $a=sqrt$, $b=sqrt$, получим такое выражение для знаменателя:

Вернёмся к нашему пределу:

В примере №1 практически сразу после домножения на сопряжённое выражение произошло сокращение дроби. Здесь перед сокращением придётся разложить на множители выражения $3x^2-5x-2$ и $x^2-4$, а уж потом перейти к сокращению. Чтобы разложить на множители выражение $3x^2-5x-2$ нужно использовать формулу №5. Для начала решим квадратное уравнение $3x^2-5x-2=0$:

Подставляя $x_1=-frac$, $x_2=2$ в формулу №5, будем иметь:

$$ 3x^2-5x-2=3cdotleft(x-left( -fracright)right)(x-2)=3cdotleft(x+fracright)(x-2)=left(3cdot x+3cdotfracright)(x-2) =(3x+1)(x-2). $$

Теперь настал черёд разложить на множители выражение $x^2-4$. Воспользуемся формулой №1, подставив в неё $a=x$, $b=2$:

Используем полученные результаты. Так как $x^2-4=(x-2)(x+2)$ и $3x^2-5x-2=(3x+1)(x-2)$, то:

Сокращая на скобку $x-2$ получим:

Всё! Неопределённость исчезла. Ещё один шаг и мы приходим к ответу:

В следующем примере рассмотрим случай, когда иррациональности будут присутствовать как в числителе, так и в знаменателе дроби.

Найдём пределы числителя и знаменателя:

Имеем неопределённость вида $frac$. Так как в данном случае корни наличествуют и в знаменателе, и в числителе, то дабы избавиться от неопределённости придется домножать сразу на две скобки. Во-первых, на выражение $sqrt+sqrt$, сопряжённое числителю. А во-вторых на выражение $sqrt-sqrt$, сопряжённое знаменателю.

Раскрывая скобки с помощью формулы №1, получим:

Возвращаясь к рассматриваемому пределу, имеем:

Осталось разложить на множители выражения $-x^2+x+20$ и $x^2-8x+15$. Начнем с выражения $-x^2+x+20$. Чтобы разложить его на множители требуется решить уравнение $-x^2+x+20=0$, а затем воспользоваться формулой №5:

Для выражения $x^2-8x+15$ получим:

Подставляя полученные разожения $-x^2+x+20=-(x-5)(x+4)$ и $x^2+8x+15=(x-3)(x-5)$ в рассматриваемый предел, будем иметь:

В следующей (второй) части рассмотрим ещё пару примеров, в которых сопряжённое выражение будет иметь иной вид, нежели в предыдущих задачах. Главное, помните, что цель использования сопряжённого выражения – избавиться от иррациональности, вызывающей неопределённость.