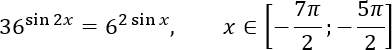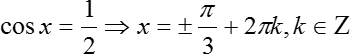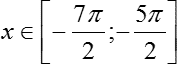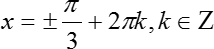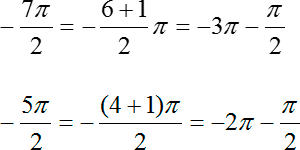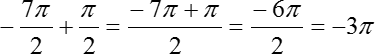Как решать уравнения с косинусами и синусами в степени

17 февраля 2014

Сегодня мы разберем еще одну комбинированную задачу из части С ЕГЭ по математике, где требуется решить уравнение, содержащее в себе и показательную, и тригонометрическую функцию.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку:

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Шаг 1: решение тригонометрического уравнения

Итак, нужно решить уравнение:

36 sin 2 x = 6 2sin x

Очевидно, перед нами комбинированная конструкция, содержащая в себе и показательное, и тригонометрическое уравнение.

Синус двойного угла

Как решать такое уравнение? Давайте для начала выпишем все тригонометрические функции, которые присутствуют в этом уравнении, а именно:

Что мы можем сказать о полученных выражениях? В первом (sin 2 x ) аргумент синуса — это 2х; а во втором (2sin x ) аргумент — просто x . Итак, аргументы наших тригонометрических функций не совпадают. Это первое, на что нужно обратить внимание при решении любого тригонометрического уравнения. Следовательно, каким-то образом нужно сделать так, чтобы аргументы стали одинаковыми. В данном случае все очень просто, ведь мы знаем формулу двойного угла:

sin 2 x = 2sin x · cos x;
36 2sin x cos x = 6 2sin x .

Решение показательного уравнения

Теперь у нас другая проблема: перед нами [показательное уравнение], в котором присутствуют функции с разными основаниями. Слева основание показательной степени 36, а справа — 6. И это еще один принципиальный момент: нам нужно сделать так, чтобы и слева, и справа основание показательной функции было одним и тем же. Для этого заметим, что 36 можно записать так:

Следовательно, мы можем переписать наше уравнение в следующем виде:

(6 2 ) 2sin x cos x = 6 2sin x

Теперь воспользуемся правилом возведения степени в степень: при возведении степень в степень, показатели этих степеней перемножаются. В нашем случае получаем:

( a 2 ) f ( x ) = a 2 f ( x ) ;
6 4sin x cos x = 6 2sin x .

Итак, мы получили классическое показательное уравнение, в котором основания степеней являются константами и равны друг другу. Следовательно, мы можем просто убрать их и записать:

4sin x cos x = 2sin x

Решение тригонометрического уравнения

Тригонометрическое уравнение, которое мы получили, содержит несколько элементов с тригонометрической функцией. Для решения такого уравнения предлагаю перенести все слагаемые в левую часть, в результате чего получим:

4sin x cos x − 2sin x = 0

В полученном уравнении присутствуют два алгебраических слагаемых, причем и в первом, и во втором имеется множитель 2sin x . Выносим 2sin x за скобку:

2sin x (2cos x − 1) = 0

Вынесение за скобку общего множителя

Обратите внимание: на этом шаге многие ученики допускают ошибку! Давайте я еще раз напомню, как выносить общий множитель за скобку. Для этого выпишем наше выражение еще раз:

4sin x cos x − 2sin x

Перепишем эту конструкцию следующим образом:

2 · 2sin x cos x − 2sin x

Отсюда нам нужно вынеси [общий множитель]. Как вообще определяется, что можно вынести множитель за скобку? Простым перебором: мы берем самое первое слагаемое в нашем выражении и рассматриваем самый первый множитель, входящий в это слагаемое. Таким множителем является число 2.

А теперь — вопрос: встречается ли множитель 2 во втором нашем слагаемом? Конечно, встречается! Значит, ее мы выносим и идем далее. Следующий множитель тоже 2, но второй двойки во втором слагаемом не имеется, поэтому еще одну двойку вынести за скобку мы не можем.

Идем дальше: множитель sin x . Присутствует ли sin x во втором слагаемом? Да, безусловно. И последний множитель из первого слагаемого — cos x . Есть ли он во втором слагаемом? Нет, такого множителя во втором слагаемом нет. Поэтому вынести за скобку множитель cos x мы не можем. Вот и все. Получается, что из нашей конструкции можно вынести за скобку лишь множители 2 и sin x .

2 · 2sin x cos x − 2sin x = 2sin x (2cos x − 1)

Но на этом проблемы не заканчиваются. Когда ученики записывают элементы в скобках, здесь часто допускаются совершенно нелепые ошибки. Поэтому всем своим ученикам я рассказываю одно и то же правило, которое [гарантировано] избавит вас от всех подобных проблем. Правило звучит следующим образом:

При вынесении за скобку общего множителя обязательно ставьте единицу на месте каждого вынесенного элемента!

Такая запись является гарантом того, что вы не допустите ошибку при вынесении множителя за скобку. Давайте посмотрим, как это правило сработает для нашего выражения. Записываем готовое разложение — и мы получили именно то выражение, которое у нас получилось в самом начале:

2 · 2sin x cos x − 2sin x = 2sin x (1 · 2 · 1cos x − 1 · 1) = 2sin x (2cos x − 1)

Решение простейших тригонометрических уравнений

С вынесением общего множителя за скобку разобрались, возвращаемся к нашему уравнению. Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю. Получаем несколько вариантов:

2 = 0; sin x = 0 (х = π n , n ∈ Z ); 2cos x − 1 = 0.

Очевидно, что уравнение 2 = 0 корней не имеет (Что за бред вообще?). Второе уравнение мы разобрали сразу, т.к. это был частный случай. Рассмотрим теперь последнее уравнение:

Уравнение решено. Мы разобрали каждый вариант, поэтому других корней не будет.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Отбор корней на отрезке

Переходим ко второй части задачи C1 — отбору корней в отрезке:

И снова предлагаю вашему вниманию небольшое усовершенствование.

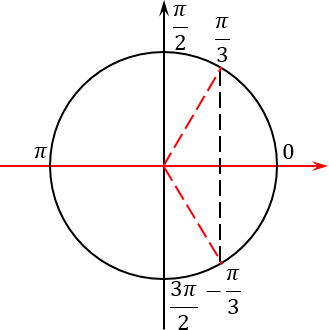
Хитрость: отмечаем корни на тригонометрическом круге

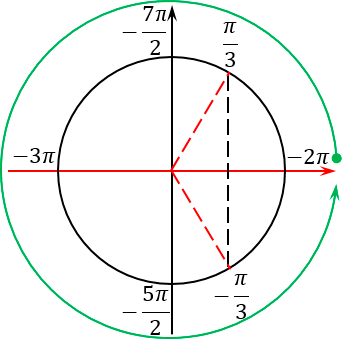
Этот прием я разработал совсем недавно вместе со своими учениками. Суть приема проста: чертим тригонометрический круг (в простонародье — радар) и отмечаем на нем наши корни. Сначала — первую группу:

Это одна точка в самом начале круга и еще одна точка, которая диаметрально противоположна исходной.

Теперь отмечаем вторую группу корней:

Поскольку период 2π k — это полный оборот окружности, никаких других точек на тригонометрическом круге точно не появится. Итого получим следующую картинку:

Все, корни мы отметили. Теперь разбираемся с концами отрезка. Давайте перепишем их в таком виде:

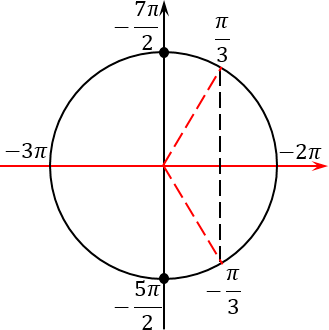
По существу, мы просто выделили целую часть — по аналогии с неправильными дробями в арифметике. Отметим эти точки на том же тригонометрическом круге:

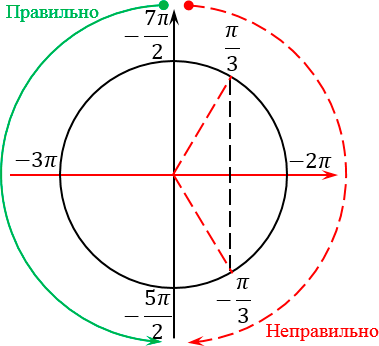
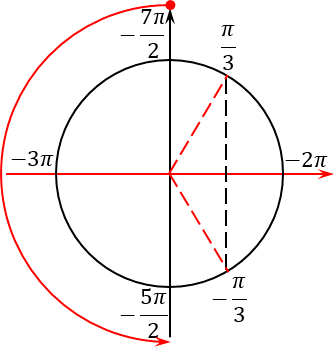
Отлично, концы искомого отрезка отмечены. Осталось грамотно отметить сам отрезок. Для этого нужно понять, как он расположен на нашем тригонометрическом круге. И вот тут многие ученики опять допускают ошибку: они путаются, в какую сторону «наматывать» этот отрезок. Ведь существует два варианта — против часовой стрелки (это правильный вариант) и по часовой (соответственно, неправильный):

На самом деле, чтобы никогда больше не путаться, нужно вспомнить основное правило: мы всегда накручиваем углы в сторону, противоположную движению часовой стрелки. Например, если бы мы хотели попасть из точки 0 в точку 2π, мы бы двигались именно против часовой стрелки:

Это правило все прекрасно помнят, когда считают значение тригонометрических функций. Но почему-то забывают, что это правило работает для любых отрезков, а не только в пределах от 0 до 2π. Поэтому еще раз смотрим на наш исходный отрезок, берем его левый конец, т. е. самое маленькое число −7π/2, и идем от него в наш второй конец против часовой стрелки:

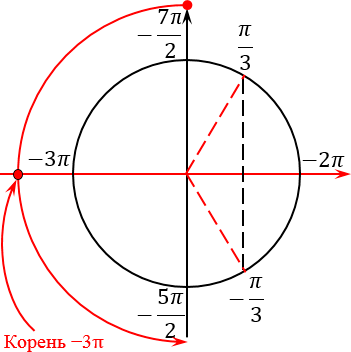
Прекрасно, отрезок отмечен. Для того, чтобы выявить интересующие нас корни, давайте продолжим лучи, проходящие через все корни, отмеченные красным, за пределы тригонометрического круга (по сути — до бесконечности). Таких лучей будет 4 штуки.

А теперь берем ручку, ставим ее в самый левый конец отрезка (точку −7π/2) и начинаем двигаться ко второму концу отрезка. Разумеется, мы тут же наткнемся на пересечение нашего отрезка и одного из лучей, отвечающих за корни. Так вот: любое такое пересечение означает, что мы нашли конкретный корень, который лежит на нашем рассматриваемом отрезке.

Возникает вопрос: как найти числовое значение этого корня? Но и тут все очень просто. Давайте подумаем: на какое расстояние нужно шагнуть из точки −7π/2, т. е. из начала нашего отрезка, чтобы попасть на горизонтальный диаметр? Очевидно, что это расстояние равно π/2. Прибавляем к концу нашего отрезка этот самый шаг:

В данном случае получилось, что этот корень уже изначально был отмечен, когда мы отмечали концы нашего отрезка: −7π/2 и −5π/2.

Если мы пойдем дальше, двигаясь из точки -3π к правому концу нашего отрезка, никаких других корней уже не встретим. Получается, что во время обхода мы столкнулись лишь с одним корнем — −3π. В принципе, это и неудивительно: в данной задаче нам попался довольно короткий отрезок, который на тригонометрическом круге занимает лишь половину полного оборота. И так уж получилось, что большинство корней, которые мы получили при решении уравнения, сосредоточены на второй половине нашего круга — в той самой, которую мы вообще не рассматривали.

В общем, не стоить удивляться, когда в процессе отбора корней у нас получился всего лишь один ответ. Это правильный ответ, и приведенный выше рисунок является полноценным тому обоснованием. Следовательно, задача решена полностью:

1. Мы решили само уравнение, последовательно разобравшись с показательным и тригонометрическим уравнением;
2. Затем отобрали те корни, которые лежат на требуемом отрезке, и обосновали этот выбор графически.

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Замечание по поводу разложения на множители

Еще один тонкий момент в решении данной задачи состоит в том, что многие ученики неправильно выносят за скобку общие множители. Но это — тема отдельного урока, который вообще не относится к ЕГЭ по математике, поэтому сегодня я коснулся данного вопроса лишь вкратце. Ровно настолько, насколько это необходимо для решения конкретной задачи.

Однако если в сегодняшнем уроке вам все равно что-то непонятно, если вы хотите решать тригонометрию еще лучше, не нужно расстраиваться, просто заходите на мой сайт berdov . com . Там вас ждет еще больше уроков, а также тесты для самостоятельного решения.

Но и это еще не все: на любой странице моего сайта справа вверху есть форма для записи на занятие. Смело заполняйте ее, указывайте свое имя, телефон и хоть немного расскажите о своей математической проблеме. И как только вы нажмете на кнопку «Записаться», буквально через несколько секунд я получу ваше сообщение, и в течение нескольких минут (максимум — нескольких часов) я вам позвоню, и мы обсудим все интересующие проблемы и составим индивидуальную программу обучения, рассчитанную именно на вас.

И вот тогда вы точно убедитесь, что математика — это, на самом деле, легко, что никаких сложных формул и теорем в ней нет. Тем более, в школьном курсе. Пишите, звоните, приходите — и будем заниматься. А у меня на сегодня все. С Вами был Павел Бердов. До новых встреч!

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Как решать уравнения с косинусами и синусами в степени

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Методы решения тригонометрических уравнений.

Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

1. Алгебраический метод.

( метод замены переменной и подстановки ).

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

Видео:12 часов Тригонометрии с 0.Скачать

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Видео:СЕКРЕТНЫЙ ЛАЙФХАК С ТРИГОНОМЕТРИЕЙ НА ЕГЭ #shorts #математика #егэ #огэ #тригонометрияСкачать

Методы решения тригонометрических уравнений

Разделы: Математика

Составной частью ЕГЭ являются тригонометрические уравнения.

К сожалению, не существует общего единого метода, следуя которому можно было бы решить любое уравнение, в котором участвуют тригонометрические функции. Успех здесь могут обеспечить лишь хорошие знания формул и умение видеть те или иные полезные комбинации, что вырабатывается лишь практикой.

Общая цель обычно состоит в преобразовании входящего в уравнение тригонометрического выражения к такому виду, чтобы корни находились из так называемых простейших уравнений:

Для этого необходимо уметь применять тригонометрические формулы. Полезно знать и называть их “именами”:

1. Формулы двойного аргумента, тройного аргумента:

сos 2x = cos 2 x – sin 2 x = 1 – 2 sin 2 x = 2 cos 2 x – 1;

sin 2x = 2 sin x cos x;

tg 2x = 2 tg x/1 – tg x;

ctg 2x = (ctg 2 x – 1)/2 ctg x;

sin 3x = 3 sin x – 4 sin 3 x;

cos 3x = 4 cos 3 x – 3 cos x;

tg 3x = (2 tg x – tg 3 x)/(1 – 3 tg 2 x);

ctg 3x = (ctg 3 x – 3ctg x)/(3ctg 2 x – 1);

2. Формулы половинного аргумента или понижения степени:

sin 2 x/2 = (1 – cos x)/2; сos 2 x/2 = (1 + cos x)/2;

tg 2 x = (1 – cos x)/(1 + cos x);

ctg 2 x = (1 + cos x)/(1 – cos x);

3. Введение вспомогательного аргумента:

рассмотрим на примере уравнения a sin x + b cos x = c а именно, определяя угол х из условий sin y = b/v(a 2 + b 2 ), cos y = a/v(a 2 + b 2 ), мы можем привести рассматриваемое уравнение к простейшему sin (x + y) = c/v(a 2 + b 2 ) решения которого выписываются без труда; тем самым определяются и решения исходного уравнения.

4. Формулы сложения и вычитания:

sin (a + b) = sin a cos b + cos a sin b;

sin (a – b) = sin a cos b – cos a sin b;

cos (a + b) = cos a cos b – sin a sin b;

cos (a – b) = cos a cos b + sin a sin b;

tg (a + b) = ( tg a + tg b)/(1 – tg a tg b);

tg (a – b) = ( tg a – tg b)/(1 + tg a tg b);

5. Универсальная тригонометрическая подстановка:

cos a = (1 – tg 2 (a/2))/(1 + (tg 2 (a/2));

tg a = 2 tg a/2/(1 – tg 2 (a/2));

6. Некоторые важные соотношения:

sin x + sin 2x + sin 3x +…+ sin mx = (cos (x/2) -cos (2m + 1)x)/(2 sin (x/2));

cos x + cos 2x + cos 3x +…+ cos mx = (sin (2m+ 1)x/2 – sin (x/2))/(2 sin (x/2));

7. Формулы преобразования суммы тригонометрических функций в произведение:

sin a + sin b = 2 sin(a + b)/2 cos (a – b)/2;

sin a – sin b = 2 cos (a + b)/2 sin (a – b)/2;

cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2;

cos a – cos b = -2 sin(a + b)/2 sin (b – a)/2;

tg a + tg b = sin (a + b)/(cos a cos b);

tg a – tg b = sin (a – b)/(cos a cos b).

А также формулы приведения.

В процессе решения надо особенно внимательно следить за эквивалентностью уравнений, чтобы не допустить потери корней (например, при сокращении левой и правой частей уравнения на общий множитель), или приобретения лишних корней (например, при возведении обеих частей уравнения в квадрат). Кроме того, необходимо контролировать принадлежат ли получающие корни к ОДЗ рассматриваемого уравнения.

Во всех необходимых случаях (т.е. когда допускались неэквивалентные преобразования), нужно обязательно делать проверку. При решении уравнении необходимо научить учащихся сводить их к определенным видам, обычно начиная с легких уравнении.

Ознакомимся с методами решения уравнений:

1. Сведение к виду аx 2 + bx + c = 0

2. Однородность уравнений.

3. Разложение на множители.

4. Сведение к виду a 2 + b 2 + c 2 = 0

5. Замена переменных.

6. Сведение уравнения к уравнению с одной переменной.

7. Оценка левой и правой части.

8. Метод пристального взгляда.

9. Введение вспомогательного угла.

10. Метод “ Разделяй и властвуй ”.

1. Решить уравнение: sin x + cos 2 х = 1/4.

Решение: Решим методом сведения к квадратному уравнению. Выразим cos 2 х через sin 2 x

4 sin 2 x – 4 sin x – 3 = 0

sin x = -1/2, sin x = 3/2(не удовлетворяет условию х€[-1;1]),

т.е. х = (-1) к+1 arcsin 1/2 + k, k€z,

Ответ: (-1) к+1 /6 + k, k€z.

2. Решить уравнение: 2 tg x cos x +1 = 2 cos x + tg x,

решим способом разложения на множители

2 tg x cos x – 2 cos x + 1 – tg x = 0,где х /2 + k, k€z,

2 cos x (tg x – 1) – (tg x – 1) = 0

(2 cos x – 1) (tg x – 1) = 0

2 cos x – 1 = 0 или tg x – 1 = 0

cos x = 1/2, tgx = 1,

т.е х = ± /3 + 2k, k€z, х = /4 + m, m€z.

Ответ: ± /3 + 2k, k€z, /4 + m, m€z.

3. Решить уравнение: sin 2 x – 3 sin х cos x + 2 cos 2 х = 0.

Решение: sin 2 x – 3 sin х cos x + 2 cos 2 х = 0 однородное уравнение 2 степени. Поскольку cos x = 0 не является корнем данного уравнения, разделим левую и правую часть на cos 2 х. В результате приходим к квадратному уравнению относительно tg x

tg x = 1 и tg x = 2,

откуда х = /4 + m, m€z,

х = arctg 2 + k, k€z.

Ответ: /4 + m, m€z, arctg 2 + k, k€z.

4. Решить уравнение: cos (10x + 12) + 42 sin (5x + 6) = 4.

Решение: Метод введения новой переменной

Пусть 5х + 6 = у, тогда cos 2у + 42 sin у = 4

1 – 2 sin 2 у + 42 sin у – 4 = 0

sin у = t, где t€[-1;1]

2t 2 – 42t + 3 = 0

t = 2/2 и t = 32/2 (не удовлетворяет условию t€[-1;1])

sin (5x + 6) = 2/2,

5x + 6 = (-1) к /4 + k, k€z,

х = (-1) к /20 – 6/5 + k/5, k€z.

Ответ: (-1) к ?/20 – 6/5 + ?k/5, k€z.

5. Решить уравнение: (sin х – cos у) 2 + 40х 2 = 0

Решение: Используем а 2 +в 2 +с 2 = 0, верно, если а = 0, в = 0, с = 0. Равенство возможно, если sin х – cos у = 0, и 40х = 0 отсюда:

х = 0, и sin 0 – cos у = 0, следовательно, х = 0, и cos у = 0, отсюда: х = 0, и у = /2 + k, k€z, также возможна запись (0; /2 + k) k€z.

Ответ: (0; /2 + k) k€z.

6. Решить уравнение: sin 2 х + cos 4 х – 2 sin х + 1 = 0

Решение: Преобразуем уравнение и применим метод “разделяй и властвуй”

(sin 2 х – 2 sin х +1) + cos 4 х = 0;

(sin х – 1) 2 + cos 4 х = 0; это возможно если

(sin х – 1) 2 = 0, и cos 4 х = 0, отсюда:

sin х – 1 = 0, и cos х = 0,

sin х = 1, и cos х = 0, следовательно

х = /2 + k, k€z

Ответ: /2 + k, k€z.

7. Решить уравнение: sin 5х + sin х = 2 + cos 2 х.

Решение: применим метод оценки левой и правой части и ограниченность функций cos и sin.

– 1 sin 5х 1, и -1 sin х 1

0 cos 2 х 1

0 + 2 2 + cos 2 х 1 + 2

2 2 + cos 2 х 3

sin 5х + sin х 2, и 2 + cos 2 х 2

-2 sin 5х + sin х 2, т.е.

sin 5х + sin х 2,

имеем левая часть 2, а правая часть 2,

равенство возможно если, они оба равны 2.

cos 2 х = 0, и sin 5х + sin х = 2, следовательно

х = /2 + k, k€z (обязательно проверить).

Ответ: /2 + k, k€z.

8. Решить уравнение: cos х + cos 2х + cos 3х+ cos 4х = 0.

Решение: Решим методом разложения на множители. Группируем слагаемые, расположенные в левой части, в пары.

(В данном случае любой способ группировки приводит к цели.) Используем формулу cos a+cos b=2 cos (a + b)/2 cos (a – b)/2.

2 cos 3/2х cos х/2 + 2 cos 7/2х cos х/2 = 0,

cos х/2 (cos 3/2х + cos 7/2х) = 0,

2 cos 5/2х cos х/2 cos х = 0,

Возникают три случая:

1. cos х/2 = 0, х/2 = /2 + k, k€z, х = + 2k, k€z;
2. cos 5/2х = 0, 5/2х = /2 + k, k€z, х = /5 + 2/5k, k€z;
3. cos х = 0, х = /2 + k, k€z.

Ответ: + 2k, /5 + 2/5k, /2 + k, k€z.

Обратим внимание на то, что второй случай включает в себя первый. (Если во втором случае взять к = 4 + 5, то получим + 2n). Поэтому нельзя сказать, что правильнее, но во всяком случае “культурнее и красивее” будет выглядеть ответ: х₁ = /5 + 2/5k, х₂ = /2 + k, k€z. (Вновь типичная ситуация, приводящая к различным формам записи ответа). Первый ответ также верен.

Рассмотренное уравнение иллюстрирует весьма типичную схему решения – разложение уравнения на множители за счёт попарной группировки и использования формул:

sin a + sin b = 2 sin (a + b)/2 cos (a – b)/2;

sin a – sin b = 2 cos (a + b)/2 sin (a – b)/2;

cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2;

cos a – cos b = -2 sin (a + b)/2 sin (b – a)/2.

Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведём решения уравнений, иллюстрирующие типичные случаи появления лишних (посторонних) корней и методы “борьбы” с ними.

Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнений. Приведём примеры.

9. Решить уравнение: (sin 4х – sin 2х – cos 3х + 2sin х -1)/(2sin 2х – 3) = 0.

Решение: Приравняем нулю числитель (при этом происходит расширение области определения уравнения – добавляются значения х, обращающие в нуль знаменатель) и постараемся разложить его на множители. Имеем:

2 cos 3х sin х – cos 3х + 2sin х – 1 = 0,

(cos 3х + 1) (2 sin х – 1) = 0.

Получаем два уравнения:

cos 3х + 1 = 0, х = /3 + 2/3k.

Посмотрим, какие k нам подходят. Прежде всего, заметим, что левая часть нашего уравнения представляет собой периодическую функцию с периодом 2. Следовательно, достаточно найти решение уравнения, удовлетворяющее условию 0 х 8 х – cos 5 х = 1.

Решение этого уравнения основывается на следующем простом соображении: если 0 t убывает с ростом t.

Значит, sin 8 х sin 2 х, – cos 5 х cos 2 х;

Сложив почленно эти неравенства, будем иметь:

sin 8 х – cos 5 х sin 2 х + cos 2 х = 1.

Следовательно, левая часть данного уравнения равна единице тогда и только тогда, когда выполняются два равенства:

sin 8 х = sin 2 х, cos 5 х = cos 2 х,

т.е. sin х может принимать значения -1, 0

Ответ: /2 + k, + 2k, k€z.

Для полноты картины рассмотрим ещё пример.

12. Решить уравнение: 4 cos 2 х – 4 cos 2 3х cos х + cos 2 3х = 0.

Решение: Будем рассматривать левую часть данного уравнения как квадратный трёхчлен относительно cos х.

Пусть D – дискриминант этого трёхчлена:

1/4 D = 4 (cos 4 3х – cos 2 3х).

Из неравенства D 0 следует cos 2 3х 0 или cos 2 3х 1.

Значит, возникают две возможности: cos 3х = 0 и cos 3х = ± 1.

Если cos 3х = 0, то из уравнения следует, что и cos х = 0, откуда х = /2 + k.

Эти значения х удовлетворяют уравнению.

Если cos 3х = 1, то из уравнения cos х = 1/2 находим х = ± /3 + 2k. Эти значения также удовлетворяют уравнению.

Ответ: /2 + k, /3 + 2k, k€z.

13. Решить уравнение: sin 4 x + cos 4 x = 7/2 sin x cos x.

Решение: Преобразуем выражение sin 4 x + cos 4 x,выделив полный квадрат: sin 4 x + cos 4 x = sin 4 x + 2 sin 2 х cos 2 х + cos 4 x – 2 sin 2 х cos 2 х = (sin 2 х + cos 2 х) 2 – 2 sin 2 х cos 2 х, откуда sin 4 x + cos 4 x = 1 – 1/2 sin 2 2х. Пользуясь полученной формулой, запишем уравнение в виде

1-1/2 sin 2 2х = 7/4 sin 2х.

обозначив sin 2х = t, -1 t 1,

получим квадратное уравнение 2t 2 + 7t – 4 = 0,

решая которое, находим t₁ = 1/2, t₂ = – 4

уравнение sin 2х = 1/2

2х = (- 1) к /6 + k, k€z, х = (- 1) к //12 + k /2, k€z .

уравнение sin 2х = – 4 решений не имеет.

Ответ: (- 1) к //12 + k /2, k€z .

14. Решить уравнение: sin 9х + sin х = 2.

Решение: Решим уравнение методом оценки. Поскольку при всех значениях а выполнено неравенство sin а1,то исходное уравнение равносильно sin х = 1 и sin 9х =1,откуда получаем х = /2 + 2k, k€z и х = /18 + 2n, n€z.

Решением будут те значения х, при которых выполнено и первое, и второе уравнение. Поэтому из полученных ответов следует отобрать только х = /2 + 2k, k€z.

Ответ: /2 + 2k, k€z.

15. Решить уравнение: 2 cos x = 1 – 2 cos 2 x – v3 sin 2х.

Решение: воспользуемся формулой:

сos 2x = cos 2 x – sin 2 x = 1 – 2 sin 2 x = 2 cos 2 x – 1;

и перепишем уравнение в виде

2 cos x = – cos 2х – 3 sin 2х.

Применим к правой части процедуру введения дополнительного аргумента. Получим уравнение:

2 cos x = – 2 (1/2 cos 2х + 3/2 sin 2х),

которое можно записать в виде

2 cos x = – 2 (cos а cos 2х + sin а sin 2х),

где очевидно, а = /3. Преобразуя правую часть полученного уравнения с помощью формулы:

cos (a – b) = cos a cos b + sin a sin b;

приходим к уравнению

2 cos x = – 2 cos (2х – /3),

cos x + cos (2х – /3) = 0.

Последнее уравнение легко решить, преобразовав сумму косинусов в произведение по формуле:

cos a + cos b = 2 cos (a + b)/2 cos (a – b)/2,

cos x + cos (2х – /3) = 2 cos (3х/2 – /6) cos (/6 – х/2) = 0

Это уравнение расщепляется на два уравнения

cos (3х/2 – /6) = 0, и

cos (/6 – х/2) = 0,

решение которых уже не представляет сколь нибудь значительных трудностей.

Ответ: 2/9(2 + 3n), 2/3(2 + 3 k), n, k€z.

16. При каких значениях параметра а, уравнение а sin x – 4 cos x = 5, имеет решения?

Решение: преобразуем левую часть уравнения, используя формулу введения дополнительного аргумента:

а sin x – 4 cos x = (а 2 + 16) sin (x – y), где y определяется из условий sin y = – 4/(а 2 + 16), и cos y = а /(а 2 + 16).

Но значение y нас не интересует. Поэтому данное уравнение перепишем в виде

(а 2 + 16) sin (x – y) = 5,

sin (x – y) = 5/(а 2 + 16), это уравнение имеет решение при условии 5/(а 2 + 16) 1.

Решим это неравенство:

5/(а 2 + 16) 1, обе части умножим на (а 2 + 16):

5 (а 2 + 16),

(а 2 + 16) 5,

а 2 + 16 25,

а 2 9, или

а 3, следовательно

а € (-;-3] U [3; ).

Ответ: (-;-3] U [3; ).

17. При каких значениях параметра а, уравнение 2 sin 2 x + 3 cos (x +2 а) = 5, имеет решения?

Решение: поскольку 0 sin 2 x 1, и -1 cos (x +2а) 1 левая часть уравнения может равняться 5 тогда и только тогда, когда одновременно выполняются равенства sin 2 x = 1, и cos (x +2 а) = 1.

Это означает, что исходное уравнение равносильно системе уравнений sin 2 x = 1, и cos (x +2 а) = 1.

sin x = – 1, sin x = 1, cos (x +2 а) = 1;

х = /2 + n, n€z, и x +2 а = 2 к, к€z;

х = /2 + n, и x = – 2 а + 2 к;

/2 + n = – 2 а + 2 к;

2 а = 2 к – /2 – n;

а = к – /4 – n/2;

а = – /4 + /2 (2к – n);

а = – /4 + m/2, m€z.

Ответ: – /4 + m/2, где m€z.

Рассмотренные выше примеры лишь иллюстрируют несколько общих рекомендаций, которые полезно учитывать при решении тригонометрических уравнений. Из приведённых примеров видно, что дать общий рецепт в каждом конкретном случае невозможно.

Ежегодно варианты экзаменационных материалов ЕГЭ содержат от 4-х до 6-ти различных задач по тригонометрии. Поэтому параллельно с повторением теоретического материала значительное время должно быть отведено решению конкретных задач, в том числе и тригонометрических уравнений. А умение можно выработать, только получив практические навыки в решении достаточного числа тригонометрических уравнений.

📸 Видео

7.5 Интегралы от тригонометрических функций / интеграл от синуса и косинуса в степениСкачать

Решение тригонометрических уравнений. Метод вспомогательного угла. 10 класс.Скачать

Косинус и синус двойного угла, часть 1. Алгебра 10 классСкачать

Как решать тригонометрические неравенства?Скачать

Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Решение тригонометрических уравненийСкачать

Как запомнить значения синусов и косинусов?! #математика #синус #косинус #геометрия #егэ #shortsСкачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать