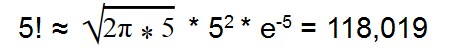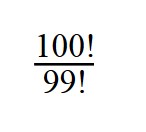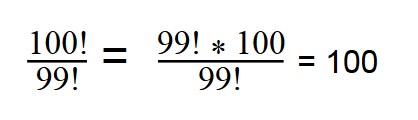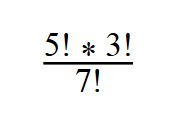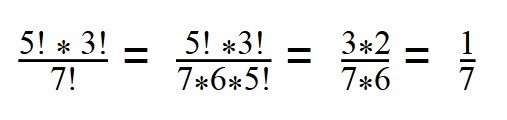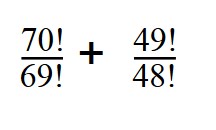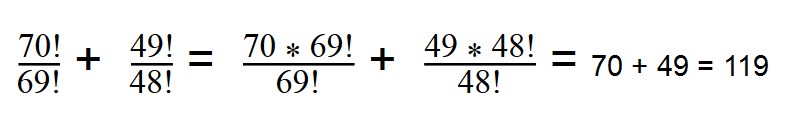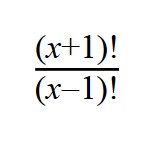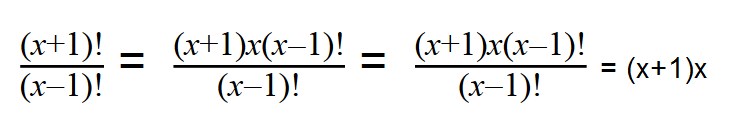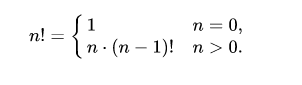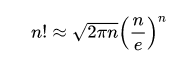О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Факториал: определение
- Формулы и свойства факториала
- Примеры решений
- Что такое уравнение с факториалом
- Формулы, упрощающие решение
- Факториал — формула, свойства и примеры решений
- Таблица факториалов
- Свойства факториалов
- Рекуррентная формула
- Комбинаторная интерпретация
- Формула Стирлинга
- Расчет по предыдущему значению
- Некоторые очень большие значения
- 🌟 Видео
Видео:Как решить уравнение с факториалами | Подходы и методы решенияСкачать

Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Видео:Сокращение дробей с факториаламиСкачать

Формулы и свойства факториала
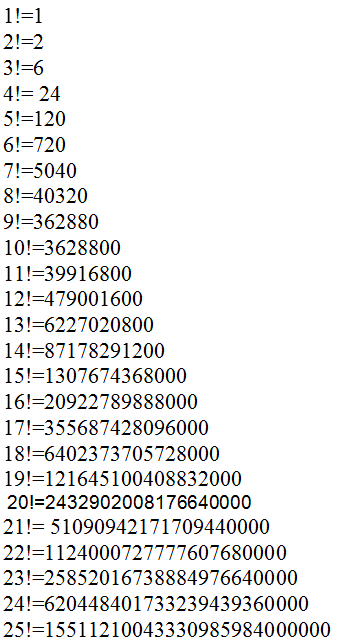
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
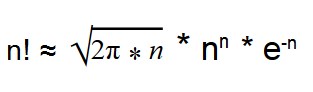 |
Рекуррентная формула
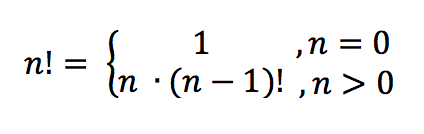 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Факториалы - быстрое вычисление | Профильная математикаСкачать

Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Что такое уравнение с факториалом
Математические выражения встречаются детям и взрослым. Распространенным выражением является факториал целого числа, который обозначается как n! и представляет собой произведение от единицы до n. Он применим только к неотрицательным значениям больше нуля, часто используется, чтобы решить задачу. Математиками было принято определение «0!», равное единице.
Понятие факториала появилось в XIX веке, с того времени были созданы таблицы, в которых описаны итоговые значения произведения чисел по каждому примеру «n!» вплоть до «25!». Данные можно использовать в готовом виде при работе, не тратя время на их повторное вычисление.
Видео:ФакториалСкачать

Формулы, упрощающие решение
Использование факториала нашло широкое применение в комбинаторике: сочетаниях, перестановке и размещениях. Проводя решение неравенств и уравнений, необходимо найти неизвестное значение. Для упрощения вычисления применяются следующие правила:
- «2n!!» равно произведению всех четных чисел 2, 4, 6, 8 и других;
- «(2n+1)!!» применяется для всех цифр вида 1, 3, 5 и подобных;
- существует равенство “2n!!*(2n+1)!!=(2n+1)!” или “2n!!*(2n-1)!!=2n!”.
Если в примере с несколькими членами уравнения имеются факториалы, то меньший из них выделяется и выносится за скобки. Это упрощает вычисление, поскольку требуется выполнить более простое произведение оставшихся параметров и общего значения. При наличии дробей, в числителе и знаменателе которых приведены факториалы, возможно их изменить с помощью нахождения одинаковой части. Она выносится за скобки, а затем сокращается.
Существует метод вычисления функций по предыдущему значению. Подсчёт показан на примере: 4! = 4 * 3! или 4 * (3*2*1). В математике старших классов школы и начальных курсов высших учебных заведений применяется Гамма-функция и бином Ньютона.
Для вычисления больших значений и решения сложных уравнений с факториалом возможно применение программного обеспечения, поскольку ручная работа с ними будет слишком трудоемкой, а онлайн-калькуляторы дают погрешность. Существуют специальные приложения и сценарии, которые вычисляют итоговое значение по заданным параметрам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Видео:ФакториалСкачать

Факториал — формула, свойства и примеры решений
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Формула факториала:
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Таблица факториалов
Видео:Решите уравнение c факториаламиСкачать

Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
🌟 Видео
Старая вступительная задача в ОксфордСкачать

ЗАГАДКИ НА ЛОГИКУ. 4 из 5 НЕ ПРОЙДУТСкачать

Решите уравнение ➜ ДВИ до ЕГЭСкачать

Что такое факториал | МатематикаСкачать

Сможешь сократить дробь с факториалами?Скачать

Комбинаторика. Основные формулы (перестановки, сочетания, размещения) и примеры решения задач.Скачать

Как решают уравнения в России и СШАСкачать

14. Вычисление пределов последовательностей ( предел с факториалом ), примеры 7, 8.Скачать

9 класс, 26 урок, Комбинаторные задачиСкачать

Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Комбинаторное уравнениеСкачать

Комбинаторика. Сочетание. 10 класс.Скачать