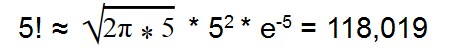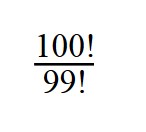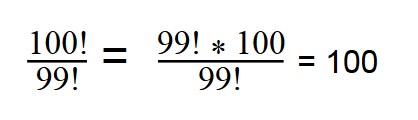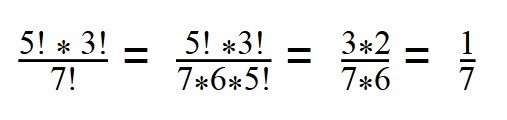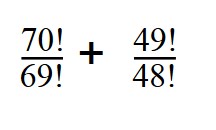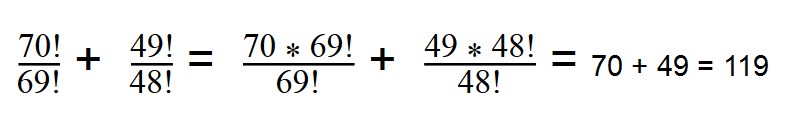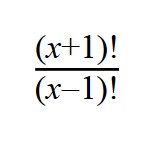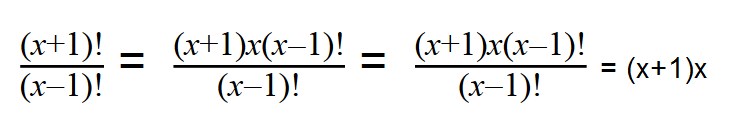Этот онлайн калькулятор вычисляет результат деления, когда и в числителе и в знаменателе находится факториал числа
Калькулятор ниже можно использовать для проверки решения примеров, когда и в числителе и в знаменателе дроби находятся факториалы, то есть, примеров на деление факториалов. Решать такие примеры довольно просто — вы выбираете больший факториал, и начинаете раскладывать его на множители до тех пор, пока не сможете сократить одинаковые факториалы и в числителе, и в знаменателе. Затем перемножаете оставшиеся множители, в примере обычно их немного.
- Калькулятор факториалов онлайн
- Что такое факториал?
- Формула для вычисления факториала
- Почему невозможно иметь отрицательный факторный фактор?
- Факториал нуля (0!) — это особый случай:
- Часто задаваемые вопросы (FAQ):
- Как рассчитать факториал в Excel?
- При чем здесь символ! иметь в виду?
- Сколько N факториалов умножить на n факториалов?
- Как мне ответить на этот вопрос? (к + 1)! + (k + 1) !?
- Заключительные слова:
- Факториал
- Факториал: определение
- Формулы и свойства факториала
- Примеры решений
- 💥 Видео
Видео:Как решить уравнение с факториалами | Подходы и методы решенияСкачать

Калькулятор факториалов онлайн
Онлайн-калькулятор факториала помогает вычислить факториал (n!) Заданного положительного числа n. Кроме того, вы можете складывать, вычитать, умножать и делить факториал двух чисел с помощью калькулятора для поиска факториалов.
Здесь для вас у нас есть факторное определение, как его вычислить, и некоторые важные материалы, которые могут лучше всего подойти для вас!
Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Что такое факториал?
В математике функция факториала (!) Называется произведением каждого положительного числа от 1 до n.
Например: если n = 5, то 5! это n! = 1 * 2 * 3 * 4 * 5 = 120. Если n = 7, то 7! равно 1 * 2 * 3 * 4 * 5 * 6 * 7 = 5040.
Что ж, вы также можете найти количество возможных комбинаций из большого набора данных с помощью онлайн-калькулятора комбинаций. И, если вы хотите определить количество возможных подмножеств из разных порядков, то калькулятор перестановок — лучший способ!
Формула для вычисления факториала
Данная формула поможет рассчитать факториал:
Где, n — это желаемое число, для которого вы хотите произвести расчеты.
Кроме того, вы можете просто добавить положительное число в онлайн-калькулятор факториалов и позволить ему просто факторизовать в течение нескольких секунд.
Рассмотрим этот бесплатный калькулятор разложения на простые множители, который помогает вычислять простые множители любого числа, создавать список всех простых чисел вплоть до любого числа.
Почему невозможно иметь отрицательный факторный фактор?
Факториальная формула ясно показывает, что она может применяться только к положительным числам, которые обязывают нас не опускаться ниже. 1. Поскольку он дает количество способов перестановки объекта, вы не можете иметь объект меньше нуля(0).
Факториал нуля (0!) — это особый случай:
Прежде всего, имейте в виду, что 0! равно одному (0!=1). Это похоже на ошибку, но это факт, поэтому это особый случай. Теперь углубимся в эту логику:
Проблема, которая возникла, когда мы собирались вычислить факториал 0 в том, что:
Мы знаем, что факториал п определяется только тогда, когда п>0, вот где и происходит путаница. Срок(0−1)!дает неопределенные результаты в математике и не имеет такого же значения, как при делении на ноль. Проблема не в том, что вы не можете его вычислить, а просто в том, что в этом нет никакого смысла. Если мы поместим значение0! к 1, мы можем получить ожидаемые значения для п!. Наш калькулятор факториалов определяет факториал нуля и других положительных целых чисел.
Видео:Факториалы - быстрое вычисление | Профильная математикаСкачать

Часто задаваемые вопросы (FAQ):
Как рассчитать факториал в Excel?
Используйте функцию=FАCТ, чтобы вычислить факториал данного числа.
При чем здесь символ! иметь в виду?
Это математическое выражение, обозначенное восклицательным знаком «! также упоминается для факториальной функции». Вы должны умножить все числа, которые существуют между числами, чтобы вычислить факториал числа.
Сколько N факториалов умножить на n факториалов?
Поскольку формула n(n−1)! означает n раз (n−1)!. Итак, чем меньше множитель, тем больше факториал N.
Как мне ответить на этот вопрос? (к + 1)! + (k + 1) !?
Вы можете ответить на этот вопрос, умножив (k+1)! к 2.
Заключительные слова:
Факториал числа может быть полезен в статистике для определения перестановки и комбинации чисел. Кроме того, когда дело доходит до исчисления, он определяет ряд Тейлора, биномиальную теорему для симметризации операций и производной n-й функции и многое другое. Просто вы можете использовать этот онлайн-калькулятор факториала, который помогает студентам, а также профессионалам вычислять факториал чисел.
Видео:Сможешь сократить дробь с факториалами?Скачать

Факториал
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:ФакториалСкачать

Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Видео:Что такое факториал | МатематикаСкачать

Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
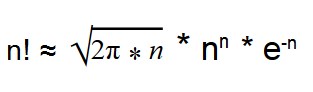 |
Рекуррентная формула
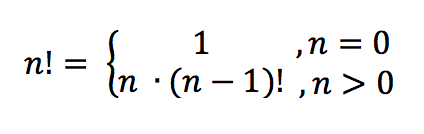 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Решите уравнение ➜ ДВИ до ЕГЭСкачать

Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
💥 Видео
Решите уравнение c факториаламиСкачать

Математика | ЗАДАЧА 22 из ОГЭ. Задачи на работуСкачать

Комбинаторика, факториал, перестановка, размещение, сочетаниеСкачать

ФакториалСкачать

Сокращение дробей с факториаламиСкачать

Факториалы — это легко! Показываю, что это такое и как решать этот примерСкачать

Комбинаторное уравнениеСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Перестановки в комбинаторике. Размещения без повторений. 9 класс.Скачать
Комбинаторика. Сочетание. 10 класс.Скачать

ОГЭ по математике. Решаем уравнения | МатематикаСкачать

Математика это не ИсламСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать