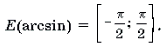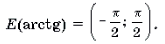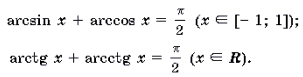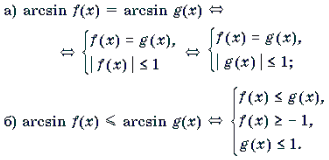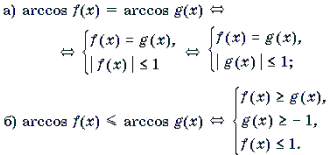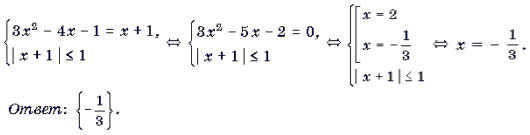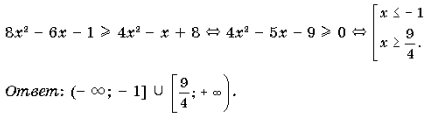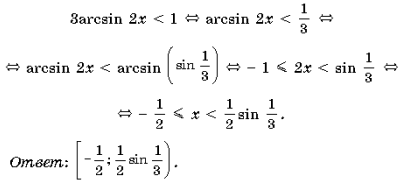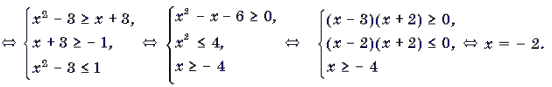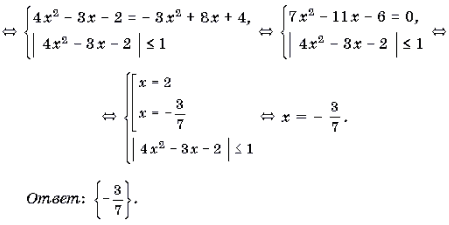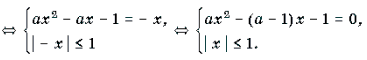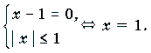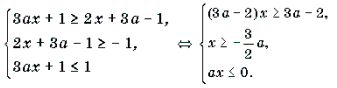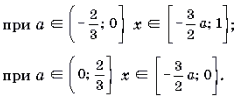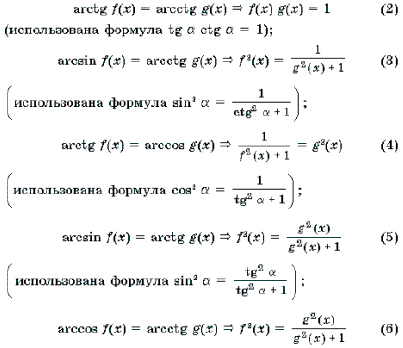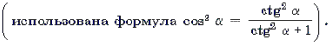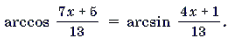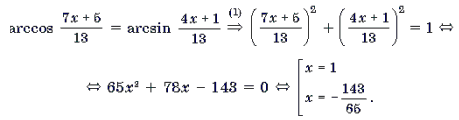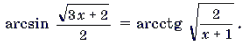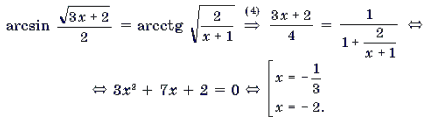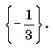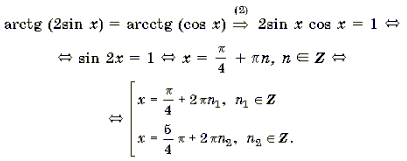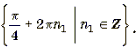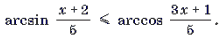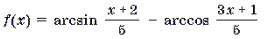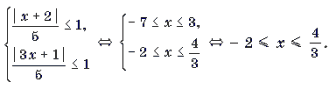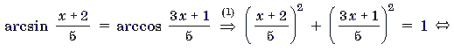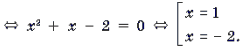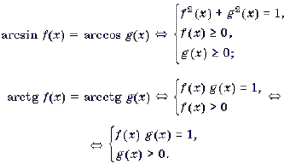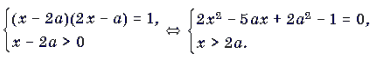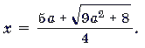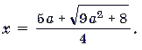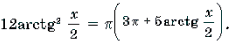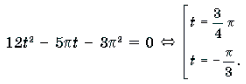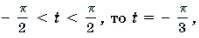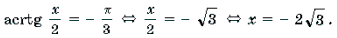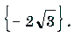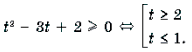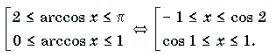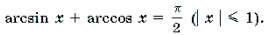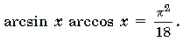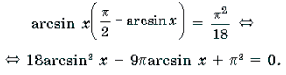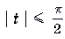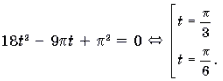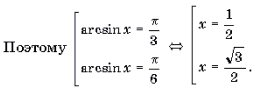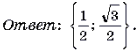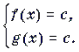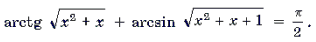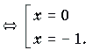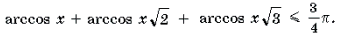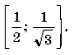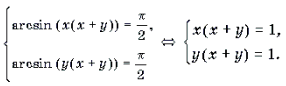Как решать уравнения с арксинусом

Арксинусом числа (a) ((a∈[-1;1])) называют число (x∈[-frac;frac]) синус которого равен (a) т.е.

Проще говоря, арксинус обратен синусу.

На круге это выглядит так:

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Как вычислить арксинус?

Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от (-frac) до (frac) ) равен аргументу арксинуса?

Например, вычислите значение арксинуса:

а) Синус какого числа равен (-frac)? Или в более точной формулировке можно спросить так: если (sin ⁡x=-frac), то чему равен (x)? Причем, обратите внимание, нам нужно такое значение, которое лежит между (-frac) и (frac). Ответ очевиден:

б) Синус какого числа равен (frac<sqrt>)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ (frac).

в) Синус от чего равен (-1)?
Иначе говоря, (sin ⁡x=-1), (x=) ?

Тригонометрический круг со всеми стандартными арксинусами:

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Arcsin, Arccos, Arctg, Arcсtg // Обратные тригонометрические функцииСкачать

Зачем нужен арксинус? Решение уравнения (sin x=a)

Чтобы понять зачем придумали арксинус, давайте решим уравнение: (sin ⁡x=frac).

Это не вызывает затруднений:

Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.

А теперь решите уравнение: (sin ⁡x=frac).

Что тут будет ответом? Не (frac), не (frac), даже не (frac) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?

Вот тут-то на помощь и приходит арксинус! Значение правой точки равно (arcsin⁡frac), потому что известно, что синус равен (frac). Длина дуги от (0) до правой точки тогда тоже будет равна (arcsin⁡frac). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному (arcsin⁡frac) от (π), то её значение составляет (π- arcsin⁡frac).

Ок, значение этих двух точек нашли. Теперь запишем полный ответ: ( left[ beginx=arcsin frac+2πn, n∈Z\ x=π-arcsin frac+2πl, l∈Zendright.) Без арксинусов решить уравнение (sin ⁡x=frac) не получилось бы. Как и уравнение (sin ⁡x=0,125), (sin ⁡x=-frac), (sin⁡ x=frac<sqrt>) и многие другие. Фактически без арксинуса мы можем решать только (9) простейших уравнений с синусом:

С арксинусом – бесконечное количество.

Пример. Решите тригонометрическое уравнение: (sin ⁡x=frac<sqrt>).
Решение:

Пример. Решите тригонометрическое уравнение: (sin ⁡x=frac<sqrt>).

Решение:
Кто поторопился написать ответ ( left[ beginx=arcsin frac<sqrt>+2πn, n∈Z\ x=π-arcsin frac<sqrt>+2πl, l∈Zendright.), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров (arcsin⁡ frac<sqrt>) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух (frac<sqrt> = frac<1 cdot sqrt> <sqrtcdot sqrt>= frac<sqrt>). Таким образом, получаем:

Значит в ответе вместо арксинусов нужно написать (frac).

Пример. Решите тригонометрическое уравнение: (sin ⁡x=frac).

Решение:
И вновь тот, кто поторопился написать ( left[ beginx= arcsin frac+2πn, n∈Z\ x=π- arcsinfrac+2πl, l∈Zendright.) на ЕГЭ потеряет (2) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать (arcsin⁡frac)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен (1) и больше или равен (-1). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.

Думаю, вы уловили закономерность.

Если (sin ⁡x) равен не табличному значению между (1) и (-1), то решения будут выглядеть как: ( left[ beginx= arcsin a +2πn, n∈Z\ x=π- arcsin a +2πl, l∈Zendright.)

Видео:Арксинус. Решение уравнения sin t = a | Алгебра 10 класс #27 | ИнфоурокСкачать

Арксинус отрицательного числа

Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:

Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:

Удивил последний пример? Почему в нем формула не работает? Потому что запись (arcsin⁡(-frac<sqrt>)) в принципе неверна, ведь (-frac<sqrt> Синус
Тригонометрические уравнения

Видео:Отбор корней с аркфункциями в №12 | Это будет на ЕГЭ 2023 по математикеСкачать

Алгебра

План урока:

Видео:10 класс - Алгебра - Арксинус. Решение уравнения sin t = aСкачать

Арккосинус

Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:

Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1 1 либо а n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.

Задание. Решите ур-ние

Задание. Запишите корни ур-ния

Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.

Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:

Ответ: 7π/3 и 8π/3.

Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние

Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:

Наконец, решениями ур-ния

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Решение уравнений tgx = a и ctgx = a

Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):

Таким образом, у ур-ния tgx = a существует очевидное решение

Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:

Задание. Решите ур-ние

Задание. Запишите формулу корней ур-ния

Далее рассмотрим ур-ние вида

Задание. Решите ур-ние

Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии

Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.

Видео:Арк-функции. Простейшие тригонометрические уравнения | Осторожно, спойлер! | Борис Трушин !Скачать

Уравнения и неравенства, содержащие обратные тригонометрические функции

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

5

Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

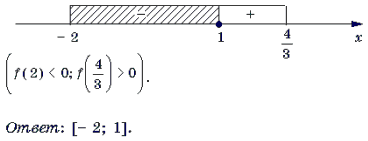
Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

2) a № 0. В этом случае уравнение системы является квадратным. Его корни: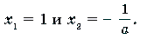
Так как | x | Ј 1, то 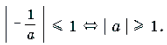. Если a = – 1, то x₂ = x₁ = 1. Если a О (– Ґ Ч ; – 1) И [1; Ґ ), то уравнение имеет два корня.

Ответ: при 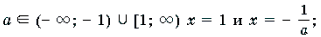при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > первое неравенство системы равносильно неравенству x і 1, при a – неравенству x Ј 1, при a = решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Ответ: при | a | > решений нет; при a = – x = 1;

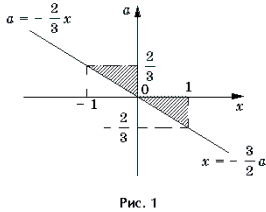
II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x₀ – решение этого уравнения. Обозначим arcsin f(x₀) = arccos g(x₀) через a. Тогда sin a = f(x₀), cos a = g(x₀), откуда f 2 (x₀) + g 2 (x₀) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x₀, для которого f(x₀) і 0 и g(x₀) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

Пример 9. Решить уравнение

Корень 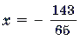является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Ответ: .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 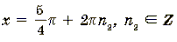являются посторонними.

Ответ:

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

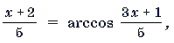
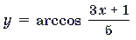
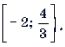
Замечание 4. Заметим, что найдя корень уравнения можно было не обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень

Ответ: при любом a

III. Замена переменной

Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Пример 14. Решить уравнение

Решение. Обозначим 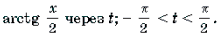После преобразований получим уравнение

Поскольку

откуда

Ответ:

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 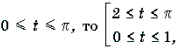откуда

Ответ: [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 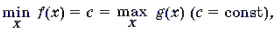то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

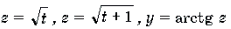
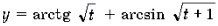
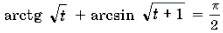
Функции являются монотонно возрастающими. Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому x 2 + x = 0

Пример 19. Решить неравенство

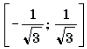
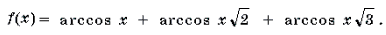
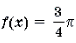
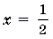
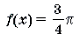
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ:

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

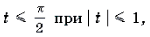
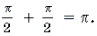
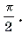
Решение. Поскольку arcsin то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.

🎥 Видео

Преобразование выражений, содержащих арксинус, арккосинус, арктангенс и арккотангенс. 2 ч. 10 класс.Скачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.Скачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Вычисление аркфункцийСкачать

Уравнение с арксинусом и арккосинусомСкачать

Задание 13 с арксинусом и арккосинусом #48Скачать

Урок 6. Простейшие тригонометрические уравнения. Арксинус/арккосинус.Скачать

10 класс, 21 урок, Обратные тригонометрические функцииСкачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Уравнение с арксинусом.Скачать