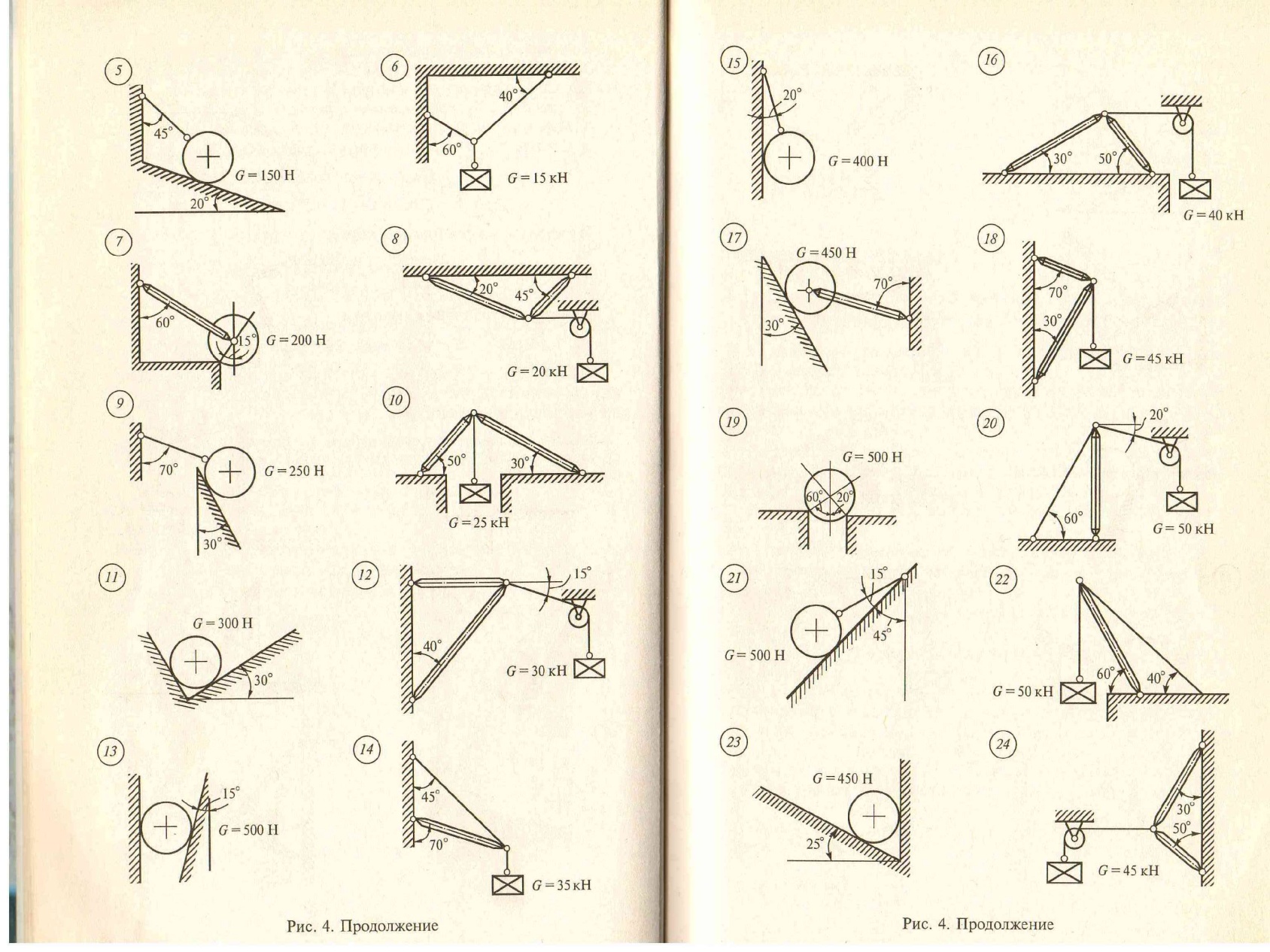
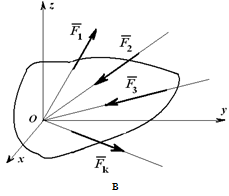
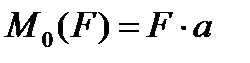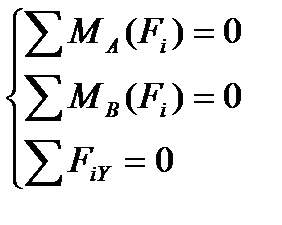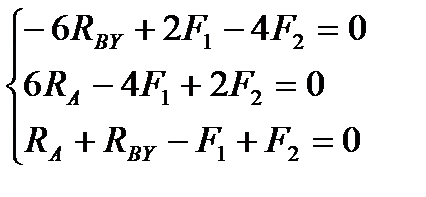Как решать уравнения равновесия пссс (6 видео)

Методика решения задач плоской системы сходящихся сил

1. Число неизвестных в данных задачах не превышает двух.

2. Рассматриваем точку, находящуюся в равновесии.

3. Определяем наличие активных сил.

4. Освобождаемся от связей и заменяем их реакциями.

5. Выбираем оси координат и располагаем в этих осях имеющиеся активные и реактивные силы.

6. Решаем уравнения равновесия относительно неизвестных.

7. Выполняем проверку.

Пример.Груз, силой тяжести F1=10Н удерживается в равновесии с помощью связей –гладких поверхностей . Определить реакции связи аналитически и графически.

Решение.

I. Аналитическое решение

1. Освобождаемся от связей, заменяя их реакциями. Получаем систему трех сходящихся в точке О сил.

2. Выбираем систему координат хОу и составляем таблицу, уравнения равновесия.

силы	=0	=0
R₁
R₂
F₁

3. Составляем систему уравнения и решаем.

Проверка: + =4,7·0,5 +8,46 ·0,9- 10=0

II. Графическое решение.

1. Выбираем масштаб 1:20 и из точки О откладываем вектор силы тяжести F₁.

2. Полученная система сил находится в равновесии, поэтому силовой многоугольник должен быть замкнут, R₁+R₂+F₁=0. Поэтому, из конца и начала вектора F проводим прямые параллельные векторам R₁ и R₂ до их пересечения.

3. Определяем реакции связей R₁ и R₂ , умножая полученные результате графического построения отрезки на масштаб.

4. Проверка: Заключается в сравнении значений векторов R₁ и R₂ , найденных аналитическим и графическим способами. r1 = (R_1а — R_1б)/ R_1а; r1 = (R_2а — R_2б)/ R_2а;

Задания для выполнения работы

Груз, силой тяжести G удерживается в равновесии с помощью связей. Определить реакции связей, удерживающих груз аналитически и графически.

Контрольные вопросы:

1. В чем отличие между осью и проекцией?

2. Сколько уравнений равновесия Вы составляли при решении задачи?

3. Методика решения задач ПССС.

4. Дайте определение плоской системе сходящихся сил.

5. Какой величиной является проекция силы на координатную плоскость?

Литература:

1. Вереин Л.И. Техническая механика – М: Академия, 2006.

2. Мовнин М.С. Основы технической механики – СПБ: Политехника, 2003.

3. Молчанова Е.В., Шурыгина Г.Н. Статика и сопротивление материалов — Томск, 2008.

Практическая работа №3

Тема урока: Определение реакций в опорах с вертикальными нагрузками

Тип урока:закрепление полученных знаний.

Цель урока:Научиться определять реакции в опорах с вертикальными нагрузками

Обеспечивающие средства:

1. методическое руководство по выполнению работы;

3.тетрадь для практических работ;

4.карандаш, линейка, ластик, авторучка;

Технология работы:

1.Внимательно изучите методические указания, предложенный теоретический материал.

2.В соответствие с вариантом, выполнить задание по методике представленной ниже.

3.Сделайте выводы о проделанной работе.

4.Ответить на контрольные вопросы.

Теоретический материал

Плоская система произвольно-расположенных сил – это система, в которой все силы лежат в одной плоскости, но линии их действия не пресекаются в одной точке.

Момент силы относительно точки

Момент –способность силы создавать вращение (М).

М_о (F) = F * а

Единица измерения М [ Н * м] 1кНм = 10 3 Нм, 1мНм = 10 6 Нм

Момент силы относительно точки равен произведению силы на перпендикуляр, опущенный из точки вращения на линию действия силы.

а – плечо, перпендикуляр или кратчайшее расстояние между точкой вращения и линией действия силы.

Если вращение тела происходит по часовой стрелке, то момент положительный.

Момент отрицательный, если вращение тела против часовой стрелки.

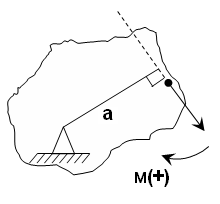
Момент силы относительно точки равен нулю, если линия действия силы проходит через точку вращения, т.к. плеча равно нулю, нет вращения.

Пример. Для двух опорной балки, нагруженной силами F₁, F₂ , определить реакции в опорах R_А и R_В. Силами тяжести балки АВ пренебречь. Опора А шарнирно-подвижная, опора В шарнирно-неподвижная.

Решение.

1. Определяем связи, заменяем их реакциями.

2. Определяем оси координат Х, У.

3. Составляем таблицу уравнения равновесия.

R_BX =0 т.к. все силы располагаются параллельно балке R_B =R_BY

Силы	=0	=0	=0
R_А	6R_A	R_A
R_BY	-6R_BY	R_BY
F₁	2F₁	-4F₁	-F₁
F₂	-4F₂	2F₂	F₂

4. Составляем уравнение по II-ому виду

Из 1-го уравнения находим R_BY

Из 2-го уравнения находим R_A

5. Проверка: по 3-му уравнению 4,7+1,3-8+2=0

Содержание

Техническая механика
Плоская система сходящихся сил
Геометрический способ определения равнодействующей плоской системы сходящихся сил
Геометрическое условие равновесия плоской системы сходящихся сил
Проекция силы на оси координат
Аналитический способ определения равнодействующей плоской системы сил
Аналитические условия равновесия плоской системы сходящихся сил
iSopromat.ru
Формы условий равновесия
Первая форма
Вторая форма
Третья форма
Другие условия равновесия
📸 Видео

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Техническая механика

Видео:Произвольная плоская система сил. Задача 1Скачать

Плоская система сходящихся сил

Геометрический способ определения равнодействующей плоской системы сходящихся сил

Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.

Теорема

Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.

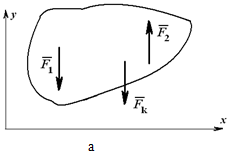
Пусть дана плоская система трех сил F₁ , F₂ и F₃ , линии действия которых сходятся в точке А (см. рисунок а) .
На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А . Сложив первые две силы F₁ и F₂ по правилу параллелограмма, получим их равнодействующую R (см. рисунок а) :
R = F₁ + F₂ .

Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F₃ :

где F_Σ – равнодействующая данной системы трех сил.

Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим:
F_Σ = F₁ + F₂ + F₃ +…+ F_n .
Сокращенно это равенство можно записать так:
F_Σ = ΣF_i , где i – все целые числа от единицы до n .

Очевидно, что построения, выполненные на рисунке a , можно заменить более простым, как показано на рисунке b . Многоугольник АВСD называют силовым многоугольником. Сторона AD , соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.

Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (см. рисунок b) .

Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.

Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.

Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.

Геометрическое условие равновесия плоской системы сходящихся сил

При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.

Очевидно, что равнодействующая F_Σ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:

и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.

Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.

Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.

Решение большинства задач статики проводят в три этапа:
— выбирают тело, равновесие которого будет рассматриваться;
— отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
— пользуясь условиями равновесия, находят неизвестные величины.

При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.

В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.

Пример решения задачи

В качестве примера решения задачи с использованием изложенных выше методов, определим натяжение веревки F и силу давления шара P на стену, если сила тяжести шара равна G .

Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:

ΣF_i = 0 , или G + N + R = 0.

Строим замкнутый силовой треугольник, начиная с изображения в произвольном масштабе вектора известной силы G (см. рисунок) . Направление обхода треугольника (т. е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения:

N = G tg α ; R = G/cos α

Искомая сила давления P шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции N стены, но направлена в противоположную сторону.
Натяжение веревки F равно по модулю ее реакции R .

Эту же задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие P (сила давления шара на стену) и F (натяжение веревки) , причем согласно аксиоме взаимодействия:

Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.

Проекция силы на оси координат

В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.

Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.

На приведенном ниже рисунке видно, что проекции силы P на оси x и y можно определить при помощи тригонометрических функций:
P_x = Pcos α, P_y = Psin α .

Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции — проекция, направленная в положительном направлении оси считается положительной, в противном случае — отрицательной.
Возможны два частных случая:
— если сила перпендикулярна оси, то ее проекция равна нулю (сила проецируется в точку) ;
— если сила параллельна оси, то она проецируется на ось в натуральную величину.

Зная проекции силы на координатные оси, можно определить ее величину (модуль) , используя теорему Пифагора, учитывая, что проекции являются катетами прямоугольного треугольника, а сама сила — гипотенузой.
Направляющий тангенс угла между вектором силы P и осью x можно определить из отношения:
tgα = P_y/P_x .

Отметим, что силу P можно представить, как равнодействующую двух составляющих сил P_x и P_y , параллельных осям координат, но эти составляющие не будут являться проекциями силы по определению, поскольку сила (в т. ч. и составляющая силы) есть величина векторная, а проекция — алгебраическая.

Аналитический способ определения равнодействующей плоской системы сил

Пусть дана плоская система сходящихся сил F₁, F₂, F₃, F₄. F_n .
Равнодействующая этой системы F_Σ = ΣF_i .

В плоскости действия данной системы сил выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось. Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е. F_Σx = ΣF_ix .
Правую часть этого равенства можно представить упрощенно: F_Σx = ΣX .

Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат x и y , алгебраически сложим проекции всех сил и найдем таким образом проекции равнодействующей:

Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:

F_Σ = √(F_Σx 2 + F_Σy 2 ) (здесь и далее √ — знак корня);

Направляющий тангенс угла между вектором F_Σ и осью x :

Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Аналитические условия равновесия плоской системы сходящихся сил

Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:

Учитывая, что F_Σx = ΣX; F_Σy = ΣY , получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил:

Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.

С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.

Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.

Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

iSopromat.ru

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Видео:Определение реакций опор простой рамыСкачать

Другие условия равновесия

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

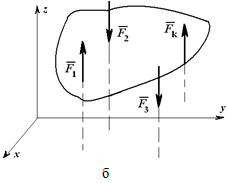
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах