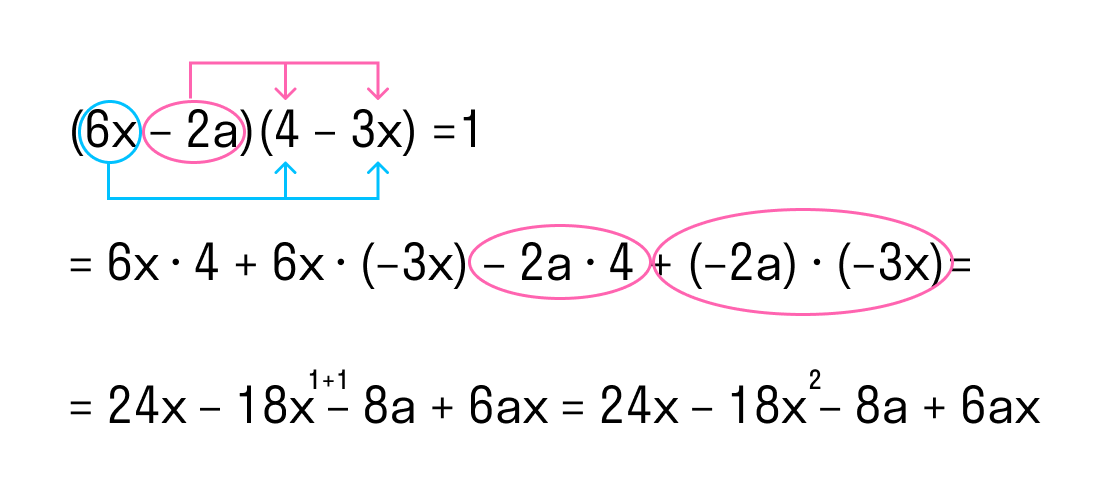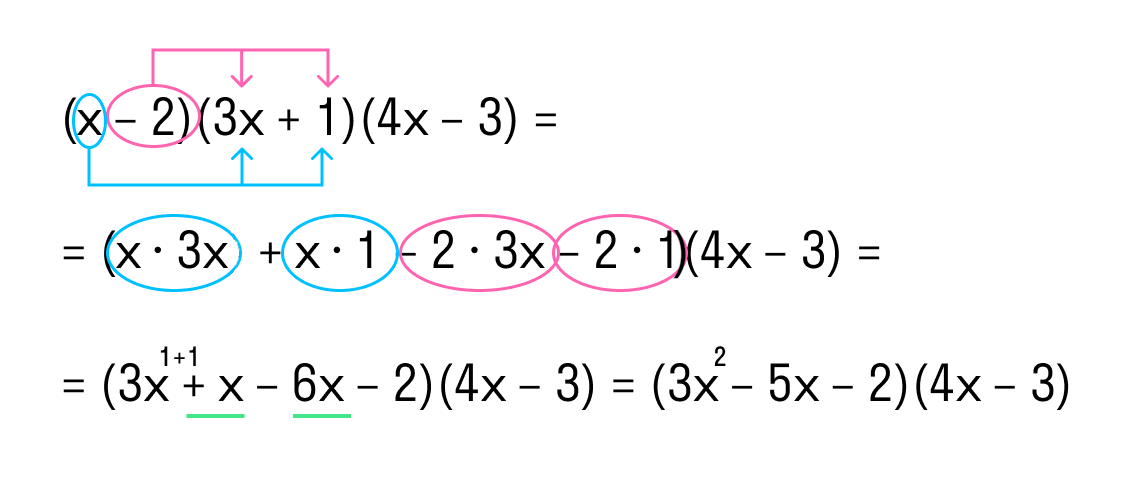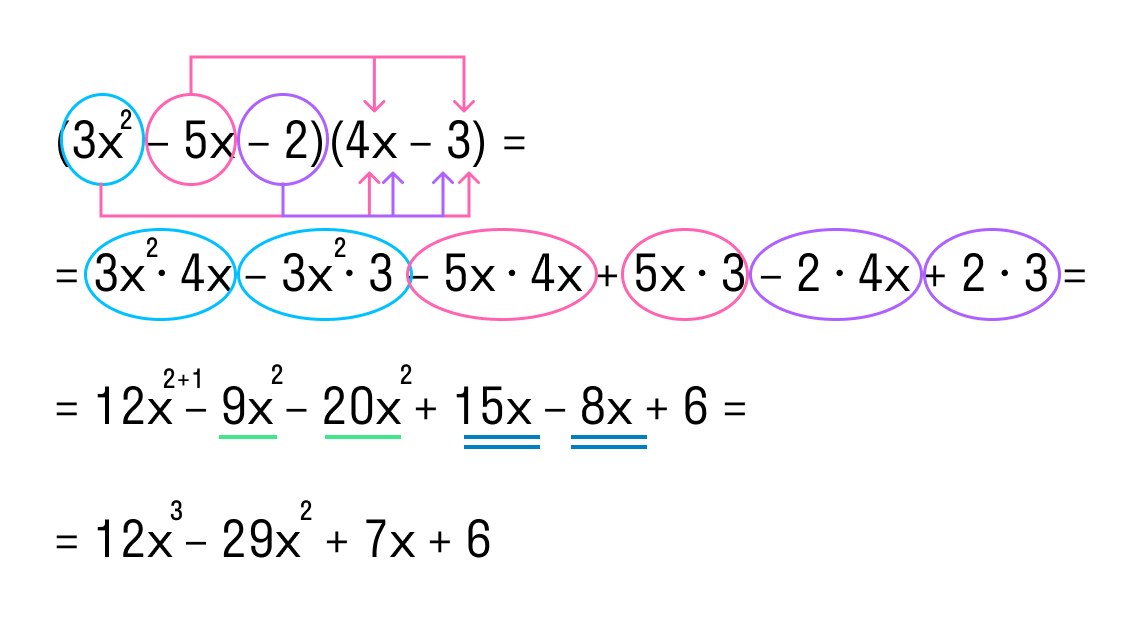Как решать уравнения по теме умножение многочлена на многочлен (8 видео)

Умножение многочлена на многочлен: правило, примеры

Одним из действий с многочленами является умножение многочлена на многочлен. В данной статье рассмотрим правило такого умножения и применим его при решении задач.

Содержание

Правило умножения многочлена на многочлен
Примеры умножения многочлена на многочлен
Умножение многочлена на многочлен
Определение многочлена
Правило умножения многочлена на многочлен
Примеры умножения многочлена на многочлен
Эта функция была отключена администратором
«Умножение многочлена на многочлен »
📺 Видео

Видео:Произведение многочленов. 7 класс.Скачать

Правило умножения многочлена на многочлен

Зададим два многочлена a + b и c + d и выполним их умножение.

В первую очередь запишем произведение исходных многочленов: поставим между ними знак умножения, предварительно заключив многочлены в скобки. Получим: ( a + b ) · ( c + d ) . Теперь обозначим множитель ( c + d ) как x , тогда выражение получит вид: ( a + b ) · x , что по сути является произведением многочлена и одночлена. Осуществим умножение: ( a + b ) · x = a · x + b · x , а затем обратно заменим х на ( c + d ) : a · ( c + d ) + b · ( c + d ) . И вновь применив правило умножения многочлена на одночлен, преобразуем выражение в: a · c + a · d + b · c + b · d . Резюмируя: произведению заданных многочленов a + b и c + d соответствует равенство ( a + b ) · ( c + d ) = a · c + a · d + b · c + b · d .

Рассуждения, которые мы привели выше, дают возможность сделать важные выводы:

Результат умножения многочлена на многочлен — многочлен. Данное утверждение справедливо для любых перемножаемых многочленов.
Произведение многочленов есть сумма произведений каждого члена одного многочлена на каждый член другого. Откуда можно сделать заключение, что при умножении многочленов, содержащих m и n членов соответственно, указанная сумма произведений членов состоит из m · n слагаемых.

Теперь можем сформулировать правило умножения многочленов:

Для осуществления умножения многочлена на многочлен, необходимо каждый член одного многочлена умножить на каждый член другого многочлена и найти сумму полученных произведений.

Видео:7 класс, 23 урок, Умножение многочлена на многочленСкачать

Примеры умножения многочлена на многочлен

В практическом решении задач нахождение произведения многочленов раскладывается на несколько последовательных действий:

запись произведения умножаемых многочленов (многочлены заключаются в скобки и между ними записывается знак умножения);
выстраивание суммы произведений каждого члена первого многочлена на каждый член второго. С этой целью первый член первого многочлена умножается на каждый член второго многочлена, затем второй член первого многочлена перемножается с каждым членом второго многочлена и так далее;
если это возможно, полученная сумма записывается в виде многочлена стандартного вида.

Пример 1

Заданы многочлены: 2 − 3 · x и x 2 − 7 · x + 1 . Необходимо найти их произведение.

Решение

Запишем произведение исходных многочленов. Получим: ( 2 − 3 · x ) · ( x 2 − 7 · x + 1 ) .

Следующим шагом составим сумму произведений каждого члена многочлена 2 − 3 · x на каждый член многочлена x 2 − 7 · x + 1 . Рассмотрим подробно: умножаем первый член первого многочлена (число 2 ) на каждый член второго многочлена, получим: 2 · x 2 , 2 · ( − 7 · x ) и 2 · 1 . Затем умножаем второй член первого многочлена на каждый член второго многочлена и получаем: − 3 · x · x 2 , − 3 · x · ( − 7 · x ) и − 3 · x · 1 . Все полученные выражения собираем в сумму: 2 · x 2 + 2 · ( − 7 · x ) + 2 · 1 − 3 · x · x 2 − 3 · x · ( − 7 · x ) − 3 · x · 1 .

Проверим, не пропустили ли мы произведение каких-либо членов: для этого пересчитаем количество членов в записанной сумме, получим 6 . Это верно, поскольку исходные многочлены состоят из 2 и 3 членов, что в общем дает 6 .

Последним действием преобразуем записанную сумму в многочлен стандартного вида: 2 · x 2 + 2 · ( − 7 · x ) + 2 · 1 − 3 · x · x 2 − 3 · x · ( − 7 · x ) − 3 · x · 1 = = 2 · x 2 − 14 · x + 2 − 3 · x 3 + 21 · x 2 − 3 · x = = ( 2 · x 2 + 21 · x 2 ) + ( − 14 · x − 3 · x ) + 2 − 3 · x 3 = 23 · x 2 − 17 · x + 2 − 3 · x 3

Кратко без пояснений решение будет выглядеть так:

( 2 − 3 · x ) · ( x 2 − 7 · x + 1 ) = 2 · x 2 + 2 · ( − 7 · x ) + 2 · 1 − 3 · x · x 2 − 3 · x · ( − 7 · x ) − 3 · x · 1 = = 2 · x 2 − 14 · x + 2 − 3 · x 3 + 21 · x 2 − 3 · x = = ( 2 · x 2 + 21 · x 2 ) + ( − 14 · x − 3 · x ) + 2 − 3 · x 3 = 23 · x 2 − 17 · x + 2 − 3 · x 3

Ответ: ( 2 − 3 · x ) · ( x 2 − 7 · x + 1 ) = 23 · x 2 − 17 · x + 2 − 3 · x 3 .

Уточним, что, когда исходные многочлены заданы в нестандартном виде, перед тем, как найти их произведение, желательно привести их к стандартному виду. Результат, конечно, будет тот же, но решение станет удобнее и короче.

Заданы многочлены 1 7 · x 2 · ( — 3 ) · y + 3 · x — 2 7 · x · y · x и x · y − 1 . Необходимо найти их произведение.

Решение

Один из заданных многочленов записан в нестандартном виде. Исправим это, приведя его к стандартному виду:

1 7 · x 2 · ( — 3 ) · y + 3 · x — 2 7 · x · y · x = — 3 7 · x 2 + 3 · x — 2 7 · x 2 · y = = — 3 7 · x 2 · y — 2 7 · x 2 · y + 3 · x = — 5 7 · x 2 · y + 3 · x

Теперь найдем искомое произведение:

— 5 7 · x 2 · y + 3 · x · x · y — 1 = = — 5 7 · x 2 · y · x · y — 5 7 · x 2 · y · ( — 1 ) + 3 · x · x · y + 3 · x · ( — 1 ) = = — 5 7 · x 3 · y 2 + 5 7 · x 2 · y + 3 · x 2 · y — 3 · x = — 5 7 · x 3 · y 2 + 3 5 7 · x 2 · y — 3 · x

Ответ: — 5 7 · x 2 · y + 3 · x · x · y — 1 = — 5 7 · x 3 · y 2 + 3 5 7 · x 2 · y — 3 · x

Напоследок проясним ситуацию, в которой есть необходимость перемножить три и более многочленов. В этом случае нахождение произведения сводится к последовательному перемножению многочленов по два: т.е. сначала перемножаются первые два многочлена; полученный результат умножается на третий многочлен; итог этого умножения – на четвертый многочлен и так далее.

Заданы многочлены: x 2 + x · y − 1 , x + y и 2 · y − 3 . Необходимо найти их произведение.

Решение

Сделаем запись произведения: ( x 2 + x · y − 1 ) · ( x + y ) · ( 2 · y − 3 ) .

Перемножим первые два многочлена, получим: ( x 2 + x · y − 1 ) · ( x + y ) = x 2 · x + x 2 · y + x · y · x + x · y · y − 1 · x − 1 · y = = x 3 + 2 · x 2 · y + x · y 2 − x − y .

Первоначальная запись произведения принимает вид: ( x 2 + x · y − 1 ) · ( x + y ) · ( 2 · y − 3 ) = ( x 3 + 2 · x 2 · y + x · y 2 − x − y ) · ( 2 · y − 3 ) .

Найдем результат этого умножения:

( x 3 + 2 · x 2 · y + x · y 2 − x − y ) · ( 2 · y − 3 ) = = x 3 · 2 · y + x 3 · ( − 3 ) + 2 · x 2 · y · 2 · y + 2 · x 2 · y · ( − 3 ) + x · y 2 · 2 · y + + x · y 2 · ( − 3 ) − x · 2 · y − x · ( − 3 ) − y · 2 · y − y · ( − 3 ) = = 2 · x 3 · y − 3 · x 3 + 4 · x 2 · y 2 − 6 · x 2 · y + 2 · x · y 3 — − 3 · x · y 2 − 2 · x · y + 3 · x − 2 · y 2 + 3 · y

Ответ:

( x 2 + x · y − 1 ) · ( x + y ) · ( 2 · y − 3 ) = 2 · x 3 · y − 3 · x 3 + 4 · x 2 · y 2 − 6 · x 2 · y + + 2 · x · y 3 − 3 · x · y 2 − 2 · x · y + 3 · x − 2 · y 2 + 3 · y

Видео:Умножение многочлена на многочлен. Алгебра, 7 классСкачать

Умножение многочлена на многочлен

О чем эта статья:

Видео:7 класс// АЛГЕБРА // Умножение одночлена на многочлен, решение уравненийСкачать

Определение многочлена

Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.

Одночлен — это произведение чисел, переменных и степеней.

Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.

Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.

Как привести многочлен к стандартному виду:

Привести к стандартному виду все одночлены, которые входят в многочлен.
Привести подобные члены.

Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:

(a + b) * (c + d) = ac + ad + bc + bd.

Правило умножения двучлена на трехчлен:

(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.

Правило перемножения трехчленов:

(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.

Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.

Видео:УМНОЖЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН. §11 Алгебра 7 классСкачать

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
Сначала составим их произведение: (a + b)(c + d).
Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
Проведем обратную замену x на (c + d):
a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd.
Как изменилось произведение исходных многочленов:
(a + b)(c + d) = ac + ad + bc + bd.
Как раз так и выглядит формула умножения многочлена на многочлен.

Правило умножения многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.

Алгоритм умножения многочлена на многочлен:

Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена. И так далее.
Сложить полученные произведения.
Преобразовать полученную сумму в многочлен стандартного вида.

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.

Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

Умножим первый многочлен на второй. Результат запишем в скобках.
Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Видео:Алгебра 7 класс. Видеоурок по теме "Умножение многочлена на многочлен" от GDZ.ruСкачать

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.

Запишем произведение: (2 − 3x)(x 2 − 7x + 1).

Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x 2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x 2 , 2(−7x) и 2*1.

Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx 2 , −3x(−7x) и −3x*1.

Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1 = 2x 2 − 14 x + 2 − 3x 3 + 21x 2 − 3x = (2x 2 + 21x 2 ) + (−14x − 3x) + 2 − 3x 3 = 23x 2 − 17x + 2 − 3x 3 .

Получается, что (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Ответ: (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.

Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.

Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Видео:Произведение одночлена и многочлена. Умножение одночлена и многочлена. 7 класс.Скачать

Эта функция была отключена администратором

Видео:7 класс // Алгебра // Умножение многочлена на многочленСкачать

«Умножение многочлена на многочлен »

Мы с Вами уже научились умножать одночлен на многочлен, если забыли как это делать , посмотрите наш урок .

Сегодня мы научимся с Вами умножать многочлен на многочлен.

Тема урока « Умножение многочленов»

Сначала давайте разберёмся как это делать . Для умножения одного многочлена на другой многочлен используют такое правило :

Правила умножения многочленов и примеры их применения

Посмотрев в примеры и изучив правило делаем важные выводы:

Результат умножения многочлена на многочлен — многочлен. Данное утверждение справедливо для любых перемножаемых многочленов.
Произведение многочленов есть сумма произведений каждого члена одного многочлена на каждый член другого.

Теперь давайте начнём сначала с того, что в заданиях 1-5 разложем многочлен на множители вынесением общего множителя за скобки. После этого обязательно сделаем проверку. Как? Умножим одночлен перед скобками на многочлен.Если мы правильно вынесли общий множитель, то должно получиться выражение , тождественно равное исходному.
Забыли как умножить одночлен на многочлен — посмотрите урок.

В остальных заданиях мы с Вами уже используя правило начинаем умножать многочлен на многочлен

Решение задач

Не забывайте при умножении одночленов использовать правило « знаков»

1) При умножении положительного числа на положительное произведение будет положительным

2) При умножении отрицательного числа на положительное произведение будет отрицательным

3) При умножении отрицательного числа на отрицательное произведение будет положительным

Задания по теме « Умножение многочленов» Уровень 1( продолжение)

При записи ответа не забывайте, что полученный многочлен обязательно должен быть записан в стандартном виде. Забыли что это значит? Посмотрите наш урок.

Умножение многочленов» Уровень 2( продолжение )

Чтобы умножить 3 или более многочленов нужно:

перемножить первые два многочлена между собой и записать результат в скобки;
умножить полученный новый многочлен из пункта 1 на следующий многочлен.

Умножение многочленов» Уровень 3( начало )

Задание по теме

Задание .Уровень 3

А теперь выполним контрольную работу

Хотите проверить знания по этой теме ? Пройдите бесплатное тестирование и получите рекомендации. Для этого перейдите по ссылке и напишите слово « тест».