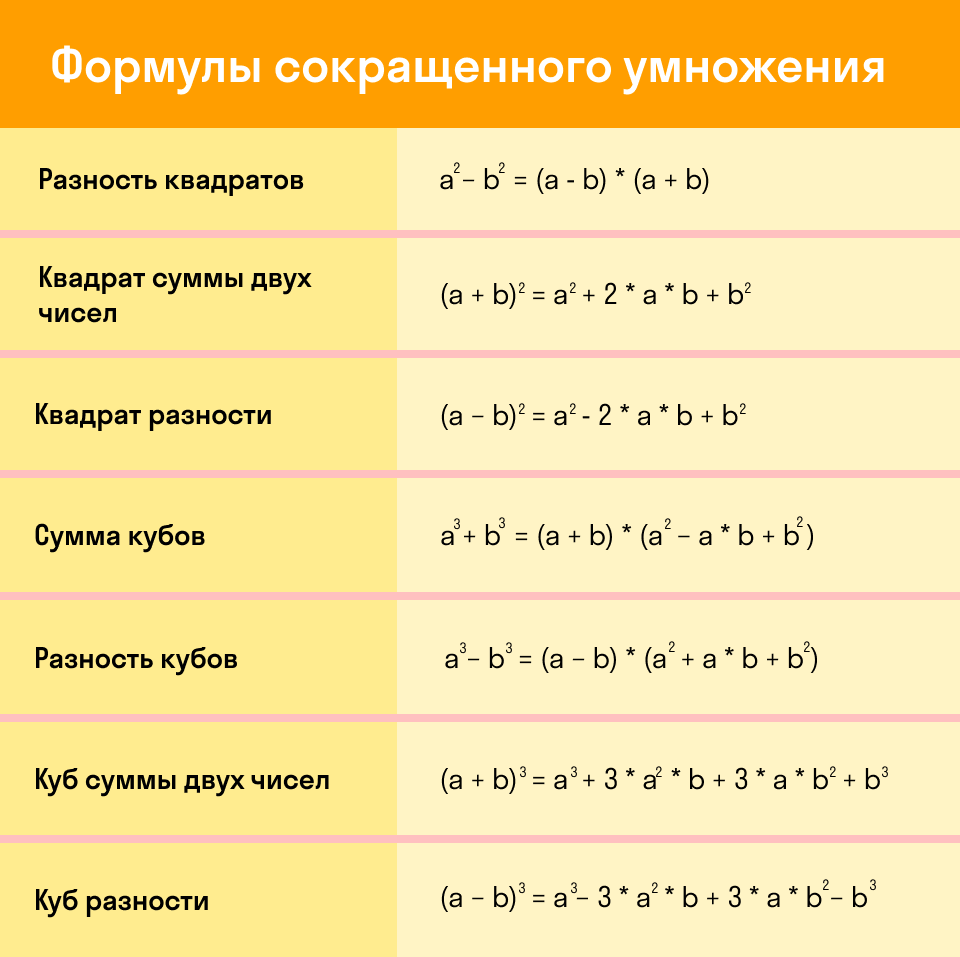
- Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
- Квадрат суммы
- Квадрат суммы: ((a+b)^2=a^2+2ab+b^2)
- Квадрат разности
- Квадрат разности: ((a-b)^2=a^2-2ab+b^2)
- Разность квадратов
- Разность квадратов (a^2-b^2=(a+b)(a-b))
- Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
- Сокращенное умножение: правила, формулы
- Формулы сокращенного умножения
- Как читать формулы сокращенного умножения
- Доказательство формул сокращенного умножения
- Дополнительные формулы сокращенного умножения
- Бином Ньютона
- Формула возведения в квадрат суммы трех, четырех и более слагаемых
- Формула разности n-ых степеней двух слагаемых
- Решение задач
- Задание 1
- Задание 2
- Задание 3
- 💥 Видео
Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
ФСУ используются при упрощении алгебраических выражений (в том числе в работе с алгебраическими дробями ), решении уравнений и неравенств , при разложении на множители и т.д. Ниже мы рассмотрим наиболее популярные формулы и разберем как они получаются.
Видео:Формулы сокращенного умножения | Математика | TutorOnlineСкачать

Квадрат суммы
Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: ((a+b)^2). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, ((a+b)^2=(a+b)(a+b)). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь , и привести подобные слагаемые. Получаем:
А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:
Квадрат суммы: ((a+b)^2=a^2+2ab+b^2)
Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.
Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ. Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.
На всякий случай отметим, что в качестве (a) и (b) могут быть любые выражения – принцип остается тем же. Например:
Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду .
Пример. Преобразуйте выражение ((1+5x)^2-12x-1 ) в многочлен стандартного вида.
Раскроем скобки, воспользовавшись формулой квадрата суммы.
…и приведем подобные слагаемые.
Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.
Пример. Вычислите значение выражения ((368)^2+2·368·132+(132)^2) без калькулятора.
Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего. Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: (a^2+2ab+b^2=(a+b)^2)
Вот теперь вычислять гораздо приятнее!
Видео:Алгебра 7. Урок 4 - Формулы сокращенного умножения и как их запомнить.Скачать

Квадрат разности
Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для ((a-b)^2):
В более краткой записи имеем:
Квадрат разности: ((a-b)^2=a^2-2ab+b^2)
Применяется она также, как и предыдущая.
Пример. Упростите выражение ((2a-3)^2-4(a^2-a)) и найдите его значение при (a=frac).
Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки .
Теперь приведем подобные слагаемые.
Вот теперь подставляем и наслаждаемся простотой вычислений.
Видео:Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать

Разность квадратов
Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:
Разность квадратов (a^2-b^2=(a+b)(a-b))
Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями .
Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус!
Попробуем воспользоваться формулой.
Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
Воспользуемся формулами степеней: ((a^n )^m=a^) и (a^n b^n=(ab)^n).
Ну, а теперь пользуемся формулой (a^2-b^2=(a+b)(a-b)), где (a=5x^2) и (b=m^5 t^3).
Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.
На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем).
Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
Теперь немного преобразуем слагаемые в скобке:
(4xy) запишем как (2·x·2y),
а (4y^2) как ((2y)^2).
Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой (a=x), (b=2y). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как (3) в квадрате.
Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой (a=(x-2y)), (b=3). Раскладываем по ней к произведению двух скобок.
И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
Видео:Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать

Тема урока: «Решение линейных уравнений, содержащих формулы сокращенного умножения»
Разделы: Математика
Цели урока:
- Обработка рациональных приёмов решения уравнений.
- Выработка умения решения задач.
- Развитие элементов творческой деятельности учащихся и умения контролировать свои действия.
- Повторение решения уравнений.
Оборудование: печатные бланки, таблица.
Тип урока: урок- семинар комплексного применения знаний, умений и навыков.
1.Организационный момент. Сообщается план семинара.
2.Сообщение по теме « Уравнение»
3. Решение линейных уравнений.
4.Сообщение о формулах сокращённого умножения.
(Работа у доски и по карточкам.)
а) Решение уравнений, содержащих квадрат суммы.
б) Решение уравнений, содержащих квадрат разности.
в) Решение квадратных уравнений, содержащих разность квадрата.
г) Решение уравнений, содержащих несколько формул.
5. Решение задачи.
6. Творческая работа учащихся.
7. Подведение итогов урока.
Ход урока.
1.Вступительное слово учителя.
Один начинающий волшебник, герой шуточной песенки, неумело обращался с заклинаниями, в результате вместо грозы у него получилась коза, а вместо утюга слон. Чтобы решить уравнение, тоже нужно совершить ряд превращений (алгебраических преобразований) и делать их нужно очень осмотрительно. Сегодня мы ещё раз увидим, какая удивительная сила заключена в формулах сокращённого умножения и как ловко они работают при решении уравнений.
Прежде всего, нужно чётко понимать, чем вы занимаетесь, когда решаете уравнение. Что, значит, решить уравнение и нужно знать, что главная задача при решении любого уравнения — свести его к простейшему.
И сегодня нам будут помогать формулы Сокращённого умножения.
2. Сообщение по теме «Уравнение»
3. Решение линейных уравнений у доски (учащиеся класса записывают решения в тетрадях)
| а) 2-3(x+2)=5-2x; 2-3x-6=5-2x, -3x+2x=5-2+6 -x =9 x=-9 Ответ:-9. | б) 20+4(2x-5)=14x+12 20+8x-20=14x+12, 8x-14x=12, -6x=12, x=-2, Ответ: -2. |
Решение уравнений по карточкам.
в) 4(2-3x)+7(6x+1)-9(9x+4)=30
г) 3-5(x+1)=6-4x.
Сообщение №2.
Слово о формулах.
4. Решение уравнений, содержащих квадрат суммы и квадрат разности.
а) x+(5x+2)2 =25(1+x2).
б) (x-6)2-x(x+8)=2.
Решение уравнений по карточкам.
в) (2-x)2-x(x+1,5)=4
г) x(x-1)-(x-5)2=2.
5. Решение уравнений, в которых содержится формула разности квадратов.
Работа у доски.
8x(1+2x)-(4x+3)(4x-3)=2x.
8x+16×2-(16×2-9)=2x,
8x+16×2-(16×2-9)=2x,
8x+16×2-16×2+9=2x,
8x-2x=-9,
6x=-9,
x=-1,5
Ответ: -1,5
Решение задачи.
Сторона первого квадрата на 2см. больше стороны второго, а площадь первого на 12 см больше площади второго. Найдите периметры этих квадратов.
Пусть x см сторона второго квадрата. Тогда(x+2) см сторона первого квадрата. Площадь первого (x+2) 2 см 2 ,а площадь второго x 2 .
Составляем уравнение:
(x+2) 2 -x 2 =12
x 2 +4x+4-x 2 =12,
4x=12-8,
4x=8,
x=2.
Если x=2,то 4x=4*2=8
Если x=2, то 4(x+2)=4(2+2)=16.
Ответ:16см,8см.
6. Решение разных уравнений, содержащих формулы сокращённого умножения.
7.Творческая работа учащихся. Заполнение таблицы.
Узнайте фамилию величайшего математика XVII века. Для этого зачеркните
буквы, не связанные с найденными ответами.
(Декарт)
| -9 | 8,2 | -2 | 3,4 | 1 | 3,1 | 1,7 | 15 | -1,5 | 17 | 11 | 3 |
| Д | П | Е | Ф | К | С | А | И | Р | Г | Ш | Т |
Приложение к уроку.
Решение линейных уравнений.
| 4(2-3x)+7(6x+1)-9(9x+4)=30 8-12x+42x+7-81-36=30, 51x-21=30, 51x=51 x=1 Ответ: 1. | 3-5(x+1)=6-4x, 3-5x-5=6-4x, -5x+4x=6-3+5, -x=8x= -8. Ответ:-8. |
Решение уравнений, содержащих квадрат суммы и квадрат разности.
| x+(5x+2) 2 =25(1+x 2 ) x+(25x 2 +20+4)=25(1+x 2 ) x+25x 2 +20x+4=25+25x 2 , 21x+25x 2 -25x 2 =25-4, 21x=21 x=1 Ответ:1. | (x -6) 2 -x(x+8)=2 x 2 -12x+36-x 2 -8x=2 -20x=2-36, -20x=-34, x=1,7 Ответ: 1,7. |
Работа по карточкам.
| (2-x)2-x(x+1,5)=4, 4-4x+x 2 -x 2 -1,5x=4, -4x-1,5x=4-4, -5,5 x=0 Ответ:0. | x(x-1)-(x-5) 2 =2 x 2 -x-(x 2 -10x+25)=2, x 2 -x-x 2 +10x-25=2 9x=27 x=3 Ответ: 3. |
Решение разных уравнений содержащих несколько формул сокращённого умножения.
| (x-4x)+(x+4)+(3x-4)(x+2)=(2x+3) 2 x 2 -16+3x 2 +6x-4x-8=4x 2 +12x+9 -10x=33 x=-3,3 Ответ:3,3. | ( 2x+3)2-4(x-1)(x+1)=49 4x 2 +12x+9-4(x 2 -1)=49 4x 2 +12x+9-4x 2 +4=49 12x+13=49 12x=36 X=3 Ответ: 3. |
8. Подведение итогов урока.
Видео:7 класс, 24 урок, Формулы сокращённого умноженияСкачать

Сокращенное умножение: правила, формулы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Решение уравнений с формулами сокращенного умножения, 7 классСкачать

Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Видео:Как раз и навсегда выучить формулы сокращенного умноженияСкачать
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Видео:Алгебра 7. Урок 5 - Формулы сокращенного умножения - применение.Скачать

Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a 2 — b 2 = (a — b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a 2 — b 2 .
Важно знать, что разность квадратов не равна квадрату разности: a 2 — b 2 ≠ (a — b) 2 .
Докажем, что a 2 — b 2 = (a — b) * (a + b).
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
a 2 — b 2 = a 2 — b 2 + ab — ab
- Сгруппируем иначе: a 2 — b 2 + a * b — a * b = a 2 — a * b + a * b — b 2
- Продолжим группировать: a 2 — a * b — b 2 +a * b = (a 2 — a * b) + (a * b — b 2 )
- Вынесем общие множители за скобки:
(a 2 — a * b) + (a * b — b 2 ) = a *(a — b) + b *(a — b)
- Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
- Результат доказательства: a 2 — b 2 = (a — b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a 2 — b 2 , нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a 2 — b 2 .
Остальные ФСУ можно доказать аналогичным методом.
Видео:РЕШЕНИЕ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ. 7 КЛСкачать

Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Видео:Формула сокращённого умножения при возведении в квадратСкачать

Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10) 2 .
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y 2 + 7 * y * x — 7 * y * x — x 2 = 49 * y 2 — x 2 .
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y) 2 — x 2 = 49 * y 2 — x 2 .
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
💥 Видео
Как запомнить формулы сокращенного умноженияСкачать

Разность квадратов двух выражений. 7 класс.Скачать

Многочлены. Формулы сокращенного умножения. Примеры ( Алгебра 7 класс )Скачать

Формула сокращенного умноженияСкачать

Сумма и разность кубов двух выражений. 7 класс.Скачать

РАЗНОСТЬ КВАДРАТОВ #shorts #егэ #математика #огэ #разность #профильныйегэСкачать

Алгебра 7 класс (Урок№32 - Применение формул сокращённого умножения. Разложение многочленов.)Скачать

Алгебра 7 класс с нуля | Математика | УмскулСкачать

Формулы сокращенного умножения | Основа 7 класса | Умскул | Средняя школаСкачать

Что такое Формулы сокращенного умножения? Для Чайников, Урок 12Скачать