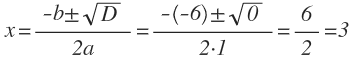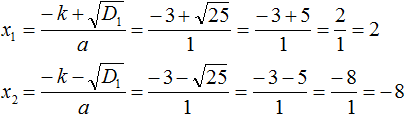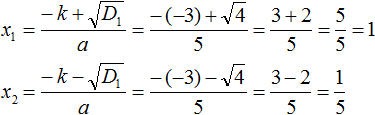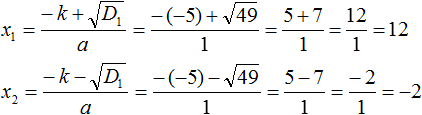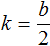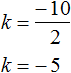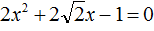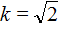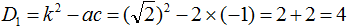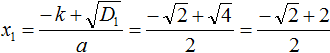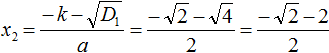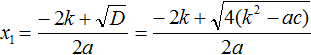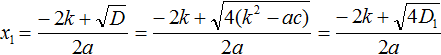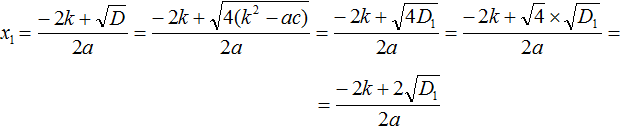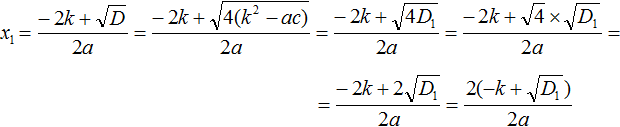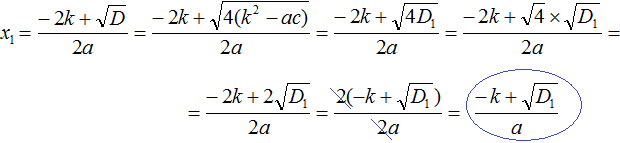Как решать уравнения по формуле d1

О чем эта статья:

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Квадратное уравнение с четным вторым коэффициентом (D1)Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k 2 − ac , а корни по формулам и .

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Примеры

Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .

Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .

Например, число 10 можно представить как 2 × 5 .

В этом произведении k = 5 .

Число 12 можно представить как 2 × 6 .

В этом произведении k = 6 .

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7 .

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .

В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k 2 − ac

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .

В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D₁ = k 2 − ac не нужно выполнять умножение числа 4 на ac .

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

Пример 5. Решить квадратное уравнение

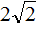
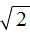
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что

Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .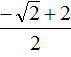

Вычислим второй корень уравнения:

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k

Теперь вычислим дискриминант по ранее известной формуле:

Вынесем в получившемся выражении за скобки общий множитель 4

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .

В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)

Но ранее было сказано, что выражение k 2 − ac обозначается через D₁ . Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Урок по алгебре на тему: «Решение квадратных уравнений по формуле D1»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Алгебра, 8 класс Урок 49

Тема урока: «Решение квадратных уравнений по формуле D 1 »

предоставить учащимся возможности познакомиться и изучить алгоритм решения полных квадратных уравнений по формуле;

способствовать пониманию и первичному закреплению алгоритма в ходе решения уравнений;

воспитывать внимательность, аккуратность, настойчивость;

повышение коммуникативной активности учащихся;

формирование умения аргументировать свою точку зрения;

разумно оценивать работу своего товарища;

1. развитие умений ставить цель, планировать и регулировать свою деятельность через решения заданий, преодолевать трудности.

2. развитие логического мышления, памяти, внимательности;

3. развивать способности учащихся к усвоению новой информации,

4. формировать умение сравнивать, анализировать, кратко и четко выражать свое мнение.

Тип урока: комбинированный урок изучения и первичного закрепления новых знаний.

Оборудование: ПК, проектор, доска, карточки, презентация.

Организационный момент (отметить отсутствующих).

Постановка целей и задач. Мотивация учебной деятельности

Сегодня у нас с вами урок изучения нового материала «Решение квадратных уравнений по формуле».

Цель урока познакомиться с алгоритмом решения полного квадратного уравнения. Девизом урока будут слова: хочу, могу, умею, делаю.

МОГУ: ребята, на уроке можно ошибаться, сомневаться, консультироваться (задавать вопросы).

УМЕЮ: мы умеем решать неполные квадратные уравнения, полные квадратные уравнения выделением квадрата двучлена.

ХОЧУ: познакомиться с алгоритмом решения полного квадратного уравнения.

ДЕЛАЮ: делаем каждый себе установку «Понять и быть тем первым, который увидит правильный путь решения». Желаю всем удачи!

3. Проверка домашнего задания.

4. Актуализация знаний учащихся.

1. Фронтальная работа с классом (в это время 3 учащихся у доски работают по индивидуальным карточкам и целью контроля выполнения домашней работы (задания – аналогичны дом. заданию).

Необходимо вспомнить теоретический материал по изученной теме «Квадратные уравнения» (что же мы умеем):

— Что такое уравнение? Что такое корень уравнения? Что значит решить уравнение?

— Какие уравнения мы называем линейными? Какие уравнения мы называем квадратными? Приведите примеры

— Сколько корней может иметь линейное уравнение (квадратное) уравнение? Примеры.

— Какие виды неполных квадратных уравнений вам известны? Приведите примеры.

— Какой общий вид имеет полное квадратное уравнение? Приведите пример.

— Какие квадратные уравнения мы с Вами умеем решать? Приведите примеры

1. Докажите, что -1 является корнем уравнения:

х 3 +1=0; х 2 -1=0; х 2 +х =0; х 2 +3х+2=0.

2. Укажите коэффициенты квадратного уравнения:

2х 2 -5х+10 = 0; 2+х+х 2 =0; х 2 +3х -0,5 =0; 5х 2 -4х =3; 0,5х 2 –х -3 =0; 8х -7 =х 2

1-3х-2х 2 =0; 11-2х 2 =4х.

3. Замените уравнение равносильным ему приведённым квадратным уравнением:

3х 2 -6х -12 =0; -х 2 +2х -2 =0;

Проверка работы по индивидуальным карточкам. Комментарии учащихся класса (по цепочке) решенных уравнений у доски. Оценка работы учащихся у доски

5. Усвоения новых знаний.

Из предыдущих уроков видно, что при решении квадратных уравнений приходилось выделять полный квадрат двучлена. Чтобы постоянно не выполнять таких преобразований, достаточно один раз выполнить эти преобразования для общего вида квадратного уравнения и получить формулу корней квадратного уравнения. Вывести формулу корней квадратного уравнения (на доске). Ввести понятие дискриминанта квадратного уравнения. Рассмотреть различные случаи решения квадратного уравнения в зависимости от значения дискриминанта (D 1 ).

Решение квадратных уравнений

D=b 2 – 4ac = 4k 2 – 4 ас =4(k 2 – ас ),

D 1 = k 2 – ас; если D 1 >0, то

х _1,2 = = = , где D 1 = k 2 – ас ,

Привести вторую запись данной формулы при условии , если в приведенном квадратном уравнении второй коэффициент чётный:

х_1,2 = (формула II ).

6. Физкультминутка (включить спокойную музыку)

Закрыть глаза, сильно напрягая глазные мышцы, на счет 1 -4, затем раскрыть глаза, расслабив мышцы глаз, посмотреть вдаль на счет 1-6. Повторить 4-5 раз.

Посмотреть на переносицу и задержать взор на счет 1-4. До усталости глаза не доводить. Затем открыть глаза, посмотреть вдаль на счет 1-6. Повторить 4-5 раз.

Не поворачивая головы, посмотреть направо и зафиксировать взгляд на счет 1-4, затем посмотреть вдаль прямо на счет 1-6. Аналогичным образом проводятся упражнения с фиксацией взгляда влево, вверх и вниз. Повторить 3-4 раза.

Перенести взгляд быстро по диагонали: направо вверх — налево вниз, потом прямо вдаль на счет 1 -6; затем налево вверх — направо вниз и посмотреть вдаль на счет 1-6. Повторить 4-5 раз.

7. Первичная проверка понимания

Работа с готовыми решениями. Комментарии трех учащихся с места

Привести пример решения квадратных уравнений.

Решить на доске : №539 (а,б)

а) 3х 2 -14х+16=0 б) 5х 2 -16х+3=0

D ₁ =7 2 -3·16=1, х _1,2 = = 2 ; 2. D ₁ =8 2 -15=49, х _1,2 = = ; 3.

8. Решение упражнений

В парах по заранее приготовленным заданиям на доске проверяют правильность выполненных уравнений.

№ 542 а) 5х 2 = 9х+2;

D = b 2 – 4 ac =81+40=121,

D >0, 2 корня: х _{1, 2} = = = 2;-0,2.

D = b 2 – 4 ac =25+56= 81; Д >0, 2 корня:

х _1,2 = = = — 7; 2

D = b 2 – 4 ac =35+36=72; Д >0, 2 корня:

х _1,2 = = = 3+3 ;3 — 3 ;

D = b 2 – 4 ac =1+80=81; D >0, 2 корня:

х _1,2 = = = 5 ; — 4

D = b 2 – 4 ac =2704 -2304=400; D >0, 2 корня:

х _1,2 = = = 36 ; -16

е) 15 у 2 -30 =22у +7;

15 у 2 -22у -37 =0;

D = b 2 – 4 ac =484 +2220=2704; D >0, 2 корня:

х _1,2 = = = -1; 2

ж) 25 p 2 -10 p +1=0;

D = b 2 – 4 ac =100-100=0; Д =0, 1 корень:

х= = 0,2 .

з) 299х 2 +100х =500- 101х 2 ;

400х 2 +100х-500 =0| : 100;

D = b 2 – 4 ac =1+80 =81; D >0, 2 корня:

х _1,2 = = = 1; -1 .

D = b 2 – 4 ac =676-100 =576; Д >0, 2 корня:

х _1,2 = = = 25 ; 1 .

D = b 2 – 4 ac =841+120= 961; D >0, 2 корня:

х _1,2 = = = -10 ; .

D = b 2 – 4 ac =16+384= 400; D >0, 2 корня:

х _1,2 = = = -8 ;12

D = b 2 – 4 ac =100-36= 64; D >0, 2 корня:

х _1,2 = = = 3 ; .

D = b 2 – 4 ac =1600+400= 2000; D >0, 2 корня:

х _1,2 = = = 20+10 ; 20 -10 ;

е) 25х 2 -13 х =10х 2 -7;

D = b 2 – 4 ac =169 -420= -259; D

9. Домашнее задание.

П. 23, читать, № 545(а-д).

10. Итог урока. Рефлексия. Выставление оценок учащимся.

Напишите формулу нахождения дискриминанта квадратного уравнения.

Напишите формулу корней квадратного уравнения

Сколько корней может иметь квадратное уравнение? От чего это зависит?

Что означает D ₁ ?

На уроке я успел сделать…

В результате я узнал и научился…

Я не понял, у меня не получилось…

Кому на уроке все было понятно встаньте и похлопайте в ладоши, у крого остались вопросы и не все получалось сразу сидя похлопайте в ладоши, у кого не получилось решить последнее уравнение

С урукин А.Н., Сочилов С.В., ЗелеРуС .А. Теляковский. Учебник. Алгебра — 8, М.: Просвещение, 2013

Урок в 8-В классе по теме «Решение квадратных уравнений по формуле D 1 » мною был проведен комбинированный урок изучения и первичного закрепления новых знаний по данной теме. В дальнейшем при изучении данной темы в 8 классе, а также сдачи ЕГЭ в 9 классе пригодятся знания, полученные на этом уроке.

Все этапы урока были направлены на достижение целей и задач, поставленных в начале урока. Урок был достаточно динамичным, насыщенным. Начало урока позволило мобилизовать учащихся класса, настроить их на восприятие нового материала. Темп работы учащихся на уроке позволяет проводить урок в достаточно быстром темпе.

Содержание учебного материала полностью соответствует программе и уровню знаний учащихся по предмету. Цели и задачи урока соответствуют плану и конспекту урока и были достигнуты.

Особенно интересно для обучающихся и продуктивно для меня на уроке получилась работа в парах. Учащиеся аргументировано отстаивали свое верное решение. Сами смогли найти ошибки одноклассников. И совместными усилиями получить верный ответ.

Во время урока большая нагрузка легла на плечи учащихся, учитель выступал в качестве координатора, несмотря на то, что это был урок «открытия» нового знания, что наиболее актуально, в связи с предстоящим введением в средней школе ФГОСов.

На уроке я использовала современные образовательные технологии: технология критического мышления – на всех этапах урока, проблемное обучение – на этапе мотивации учащихся была поставлена проблема поиска наиболее рационального способа решения полных квадратных уравнений, технология обучения в сотрудничестве (работа в парах) – взаимопомощь, взаимопроверка, информационно-коммуникативные технологии – использование во время урока презентации(авторская разработка) и, конечно, здоровьесберегающая технология – физкультминутка (гимнастика для глаз).

В целом урок в 8-В классе прошел успешно. Цели и задачи, поставленные в начале урока, были достигнуты. Учащиеся ушли с урока с хорошим настроением.

🎥 Видео

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

1 Как решать уравнения всех видов Решите уравнение Виды уравнений МАТЕМАТИКА ОНЛАЙНСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Формула корней квадратного уравнения – 8 класс алгебраСкачать

Формулы сокращенного умножения | Математика | TutorOnlineСкачать

8 класс, 25 урок, Формула корней квадратного уравненияСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Алгебра 8 класс. Ещё одна формула корней квадратного уравненияСкачать

Математика | Кубические уравнения по методу СталлонеСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать