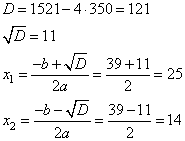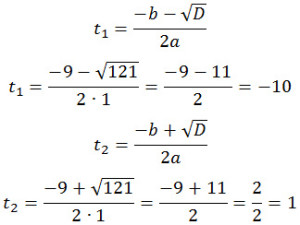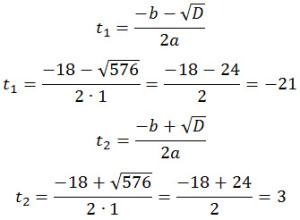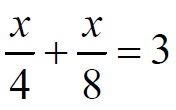ОГЭ по математике сложнее, чем базовый уровень ЕГЭ по этому же предмету, поэтому после сдачи экзамена девятиклассникам и море по колено. Сложность в разы повышается из-за того, какую особенность имеет, в отличие от базы, ОГЭ по математике — вторая часть. Но если научиться ее решать, получить «отлично» за экзамен будет проще простого!
Видео:ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Что из себя представляет вторая часть ОГЭ по математике
В ОГЭ по математике вторая часть включает шесть заданий повышенной сложности (по три на алгебру и геометрию). Для их решения требуются несколько основных навыков:
- умение решать уравнения, неравенства, их системы,
- умение преобразовывать выражения,
- умение строить и читать графики, а также простые математические модели,
- умение работать с фигурами, векторами, координатами,
- умение доказывать приведенное положение,
- умение оценивать суждения на правильность или ошибочность.
Наиболее сложными заданиями являются №22 (алгебра, функции и их свойства) и №25 (геометрия, задача). Для отметки «отлично» достаточно решить правильно все остальное и один из этих номеров.
Видео:Вторая часть ОГЭ 2022 по математике | Разбор вариантаСкачать

Критерии оценивания
Максимальный балл — это 12 из 31 балла (по два за каждый номер).
Максимальный балл ставится за полное решение, без ошибок и с верными ответами.
Один балл ставится при наличии описки или вычислительной ошибки, с учетом которой ход решения остается верным. В таком случае, ответы могут не совпадать с ключами.
Если же задание выполнено неверно полностью, то ставится ноль баллов.
Видео:Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Задания из второй части
В ОГЭ по математике вторая часть включает три алгебраических номера и три геометрических задачи. При этом, задания № 20-21 (алгебра), № 23-24 (геометрия) одного уровня сложности, а № 22 (алгебра), №24 (геометрия) — труднее.
Видео:Как решать неравенства в задании №20 во второй части ОГЭ по математике? Подробный разбор!Скачать

Как решать вторую часть ОГЭ по математике в 2021
В ОГЭ по математике вторая часть содержит шесть номеров, первый из которых (№20) проверяет умение работать с уравнениями, неравенствами, их системами, а также производить вычисления и преобразования. Оно представлено в качестве примера, который необходимо решить. Стоит следить за наличием минуса (и его сокращением), а также помнить правила преобразования выражений, действий с дробями. Не стоит полагаться исключительно на умение считать в уме: лучше считать на бумаге и после производить проверку (подставляя значение на место неизвестной в уравнениях и производя смежные действия (сложение-вычитание, деление-умножение) в простых примерах). Также нужно помнить простейшие алгоритмы решения примеров: сначала действия в скобках, а потом остальные; первыми идут умножение и деление, потом сложение и вычитание. Так, в дробях ни в коем случае нельзя забывать про знаменатель, а сокращаться из числителя и знаменателя могут только множители (простые числа и выражения в скобках).
При решении неравенств не стоит забывать о нахождении ОДЗ и знаках промежутков. При переносе на другую сторону знак меняется на противоположный: минус на плюс. При умножении на отрицательное число знак также меняется: минус на плюс, плюс на минус; больше на меньше, меньше на больше.
На ОГЭ по математике вторая часть может удивить системой. В таком случае можно сложить уравнения системы (первый член с первым, второй со вторым, третий с третьим, ответ с ответом), вывести одну из неизвестных из исходного уравнения и поставить в получившееся в результате сложения для решения.
Задание №22, которое включает в себя на ОГЭ по математике вторая часть, проверяет умение решать текстовые задачи. Их пять видов:
- Движение по воде — важно понять, как движется лодка (по течению или против него); если по течению, то скорость движения — это скорость лодки и скорость течения; если против, то скорость лодки минус скорость течения. Плот собственную скорость не имеет.
- Проценты и сплавы — важно понять, что процент повышения или понижения стоимости или концентрации вычисляется от старой, а не новой цены или концентрации, поэтому принимать новую за 100% и исходить из нее ошибочно. Новая цена — это 100% ± процент повышения (+) или понижения (-).
- Совместная работа — нужно сразу узнать, какое количество работы выполняется в час одним из действующих лиц, а совместная работа станет суммой их работы за час, умноженной на время.
- Движение по прямой — важно нарисовать себе рисунок, чтобы представлять, что и как движется. Формула, которая поможет решить любую задачу: путь — это скорость на время.
- Другие задачи — встречаются редко и интуитивно понятны.
В ОГЭ по математике вторая часть алгебры заканчивается номером на построение графика функции и определения какой-либо из ее характеристик. В этом задании важнее всего построить график, так как за его правильное построение можно получить балл, даже не ответив на вопрос, а при ошибке в построении автоматически ставится ноль. Наиболее распространенные графики — параболы (степени), гиперболы (х в знаменателе дроби), непрерывные функции (тригонометрические).
Геометрия начинается с решения задачи №23 на вычисление и №24 на доказательство. Чаще всего они связаны с теоремами о треугольнике: прямые углы, биссектрисы, медианы, высоты и пр. Реже встречаются просто углы, окружности, четырехугольники. для решения этого задания необходимо уметь ориентироваться в теоремах и аксиомах, знать основные свойства фигур и углов.
Для заключительного задания ОГЭ по математике вторая часть приготовила целый набор фигур. Чаще всего, это окружность, вписанная в фигуру или описанная вокруг нее. Особенность этой задачи в том, что для ее решения недостаточно будет одной или двух теорем: она потребует целую цепь выводов, сделанных на основе более сложных аксиом и свойств. В ее решении поможет практика.
Таким образом, ОГЭ по математике — это непростой экзамен, требующий особой подготовки. Для получения отметки «отлично» потребуется приложить массу усилий и усвоить огромное количество заданий, и хорошо иметь наставника на этом нелегком пути. Он сможет рассказать об алгоритмах решения задач и показать принципы их работы на практике. А это — залог «пятерки».
Видео:Как решить вторую часть на максимум? | Математика ОГЭ 2023 | УмскулСкачать

ОГЭ по математике: 2 часть
Смотрите бесплатные видео-уроки по теме “ОГЭ 2 часть” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
На этой странице я буду публиковать бесплатные видео-уроки по теме 2 часть ОГЭ по математике.
Задание 21: уравнения
Для того, чтобы научиться решать уравнения в 21 задании во 2 части ОГЭ по математике необходимо сначала научиться решать самые простые уравнения:
Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Задание №21 ОГЭ по математике
В двадцать втором задании необходимо решить задачу, составив уравнение с неизвестными. Ниже мы приводим алгоритмы решения типовых вариантов.
Алгоритм решения:
- Введем неизвестную величину: скорость третьего.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Выясняем, на какой
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
1. Обозначим через x км/ч скорость третьего велосипедиста. 2. Составим таблицу их краткого условия:
| v, км/ч | t, ч | S, км |
| 1 велосипедист | 21 | На 2 ч раньше всех |
| 2 велосипедист | 15 | На 1 ч раньше третьего |
| 3 велосипедист | х |
3. Задача на движение водном направлении, значит, для определения совместной скорости (сближения), необходимо из большей скорости вычитать меньшую. Наибольшая скорость была у третьего велосипедиста, потому что он догонял двух других.
4. Перед тем, как выехал третий велосипедист, первый двигался уже 2 часа. За это время он проехал 42 км, а второй проехал 15 км, поскольку был в пути 1 час. Совместная скорость третьего и второго велосипедистов равна (x-15) км/ч. так как они движутся в одном направлении. Третий велосипедист догнал второго спустя 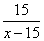
Совместная скорость третьего и первого велосипедистов равна (x-21)км/ч. Третий велосипедист догнал первого через 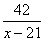
По условию третий велосипедист догнал первого спустя 9 ч после того, как догнал второго.
5. Исходя из этого, составим равенство:
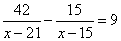
Преобразуем полученное уравнение:
6. Получили квадратное уравнение. Решим его:
По условию скорость третьего велосипедиста была наибольшей, значит, второй
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста.
2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 15 | t +7 |
| 2 велосипедист | 10 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км.
Скорость второго велосипедиста 10 км/ч. В пути он находился t + 1 часов к моменту встречи с третьим велосипедистом. Тогда в момент встречи велосипедисты находились на расстоянии 10·(t + 1) км от поселка. Расстояния эти одинаковы, значит, x·t = 10·(t + 1).
Первого велосипедиста третий догонит через t + 5 ч – время, за которое он догнал первого велосипедиста после второго, тогда до места встречи с первым велосипедистом третий проехал x·(t + 5) км.
Первый велосипедист ехал со скоростью 15 км/ч и был в пути до встречи с третьим t + 7 часов, потому как выехал он на 2 часа раньше. Расстояние, которое проехал первый велосипедист, равно 15·(t + 7) км.
Получаем еще одно равенство: x·(t + 5) = 15·(t + 7)
4. Составляем систему уравнений:
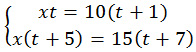

Подставляем вместо x в первое уравнение системы правую часть равенства и решаем полученное уравнение.
(t + 19)·t = 10t + 10
t 2 + 19t = 10t + 10
По формуле дискриминанта и корней:
D = 9 2 — 4·1·(-10) = 81 + 40 = 121
Первый ответ не может удовлетворять условию задачи, поскольку время не может иметь отрицательных значений. Следовательно,
x = t + 19 = 1 + 19 = 20
Скорость третьего велосипедиста 20 км/ч.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Введем неизвестные величины: скорость третьего и время его движения.
- Составим краткую запись в виде таблицы, где разместим данные в графы: скорость, время, расстояние.
- Используя условие, формулы времени или скорости, выражаем через неизвестные величины все остальные.
- Исходя из условия, составляем равенства.
- Составляем и решаем систему уравнений.
- Определяем величины, которые еще нужно найти.
- Записываем ответ.
Решение:
1. Пусть x км/ч – скорость третьего велосипедиста, а t ч – время, за которое он догнал второго велосипедиста. 2. Составим таблицу данных условия:
| v, км/ч | t, ч | s, км |
| 1 велосипедист | 24 | t +9 |
| 2 велосипедист | 21 | t +1 |
| 3 велосипедист | х | t |
3. До места встречи со вторым велосипедистом третий проехал x·t км. Второй велосипедист до момента, когда его догонит третий велосипедист, двигался t + 1 часов . Он проехал до места встречи 21·(t + 1) км. Расстояния, пройденные велосипедистами, одинаковы. Получим первое равенство x·t = 21·(t + 1). Третий велосипедист до момента встречи с первым велосипедистом после встречи о вторым, ехал t + 9 ч тогда до места встречи с первым велосипедистом он проехал расстояние x·(t + 9) км. Первый велосипедист до встречи с третьим ехал t + 11 часов, поскольку до момента выезда третьего, уже проехал 2 часа. До места встречи он проехал 24·(t + 11) км. Расстояния одинаковы. Тогда получим еще одно равенство: x·(t + 9) = 24·(t + 11) Составим систему уравнений для решения задачи: 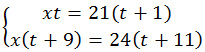
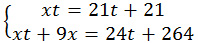
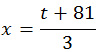
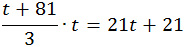
t 2 + 81t = 63t + 63
t 2 + 18t – 63 = 0
D = 18 2 — 4·1·(-63) = 324 + 252 = 576
Первое значение не подходит, поскольку время по условию не может иметь отрицательные значения. Значит, 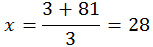
pазбирался: Даниил Романович | обсудить разбор | оценить
Пусть искомое расстояние равно x км. Скорость лодки при движении против течения равна 4 км/ч, при движении по течению равна 8 км/ч. Время, за которое лодка доплывёт от места отправления до места назначения и обратно, равно
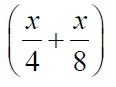
Из условия задачи следует, что это время равно 3 часам. Составим уравнение:
Решая уравнение, получаем x = 8.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Находим число процентов (или долю) твердого вещества в свежих фруктах. Находим эту величину в кг.
- Вычисляем кол-во процентов твердого вещества в сушеных фруктах.
- Составляем пропорцию и определяем общую массу сушеных фруктов.
Решение:
В сушеных фруктах масса твердого вещества, по сравнению со свежими, не меняется (а только снижается объем воды). Поэтому в искомой массе сухих фруктов мякоти тоже будет 4,2 кг. Но в процентном соотношении эта масса составит 100%–30%=70% (30% по условию приходится на воду). Искомая же (общая) масса сухих фруктов в данном случае – это 100%.
Тогда обозначим искомую массу через Х и составим пропорцию: 4,2 кг – 70% Х – 100%
Решим эту пропорцию:
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Вводим переменные-обозначения для скорости наполнения резервуара (л/мин) и для времени наполнения (мин). Выражаем через соответствующие переменные параметры наполнения для 1-й и 2-й труб.
- Составляем систему уравнений (1-е уравнение для первой трубы, 2-е – для второй).
- Решаем систему.
Решение:
Обозначим через х скорость наполнения 1-й трубы (это наша искомая величина). Тогда скорость наполнения 2-й трубы равна (х+5).Обозначим через t время наполнения 2-й трубы. Тогда время наполнения 1-й трубы составит (t+2).
Через каждую из труб должно пройти 200 л воды. Для 1-й трубы получим:
Аналогично для 2-й трубы:
Из уравнения для 2-й трубы выразим t через х:
Подставим полученное для t выражение в уравнение для 1-й трубы: 
Корень х2 не может быть принят в качестве ответа, поскольку он не удовлетворяет условию (скорость наполнения резервуара не может быть отрицательной величиной).
Значит, искомая скорость наполнения равна 20 л/мин.
pазбирался: Даниил Романович | обсудить разбор | оценить
Составим для удобства решения таблицу, в которую внесем данные из условия задачи, обозначив переменной х неизвестную величину – скорость 1 автомобиля:
| Скорость | Время | Расстояние | |
| 1 автомобиль | х | 800 х . . | 800 |
| 2 автомобиль | х – 36 | 800 х − 36 . . | 800 |
Пояснения к заполнению таблицы:
Так как мы обозначили за х скорость 1 авто, значит скорость 2 авто будет на 36 км/ч меньше.
Расстояние у каждого авто будет 800 км.
Для нахождения времени надо расстояние разделить на скорость, поэтому мы получили дроби с переменной в знаменателе.
Зная, что первый прибывает к финишу на 5 ч раньше второго, составим и решим уравнение:
800 х − 36 . . − 800 х . . = 5
Приведем к общему знаменателю х(х-36) наше уравнение и решим его:
800х – 800х+28800=5х 2 – 180
5х 2 – 180 – 28800 =0; разделим на 5 каждый коэффициент:
Решим полученное квадратное уравнение
D=b 2 – 4ac=36 2 – 4 ∙ ( − 5760 ) =24336
х1,2= − b ± √ D 2 a . . = 36 ± 156 2 . .
Отсюда х1=96, а х2 не удовлетворяет условию задачи, так как оно отрицательное, а скорость не может быть выражена отрицательным числом.
Значит, скорость первого автомобиля 36 км/ч
pазбирался: Даниил Романович | обсудить разбор | оценить
🔍 Видео
Задачи на движение из второй части. Задание 21 | Математика ОГЭ 2023 | УмскулСкачать

Задание 20 ОГЭ математика 2024 2 часть. Кубические уравненияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнения второй части. Задание №20 | МАТЕМАТИКА ОГЭ 2023 | PARTAСкачать

5 основных заданий из №20 из ОГЭ | Математика | TutorOnlineСкачать

Самое легкое решение 22 задания на ОГЭ по математике | Молодой РепетиторСкачать

2 часть ОГЭ по математике 2024 Вариант 1 ЯщенкоСкачать

Задание №9 на ОГЭ. Как решать уравнения? Какие типы будут?Скачать

17 задание из ОГЭСкачать

Как сдать ОГЭ по математике за 4 минуты? | УмскулСкачать

Разбор реального варианта ОГЭ по математике 2024 на 5 за часСкачать

Все типы 20 задания ОГЭ по математике | Молодой репетиторСкачать

УРАВНЕНИЯ ВО ВТОРОЙ ЧАСТИ ОГЭ 2024Скачать

ОГЭ. НЕРАВЕНСТВА N-20, ЧАСТЬ-2Скачать