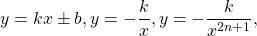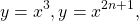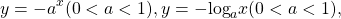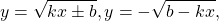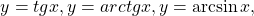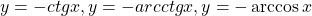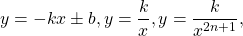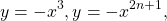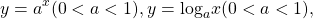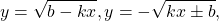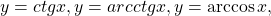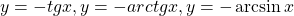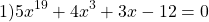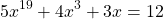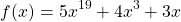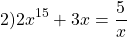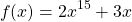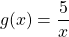Как решать уравнения используя свойства монотонности

Видео:Алгебра 10 класс. 9 сентября. Исследование функции на монотонность, используя свойства числовых неСкачать

Использование свойства монотонности функции при решении уравнений

Разделы: Математика

Цели:

Задачи:

Оборудование: карточки с заданиями для каждого ученика.

Организационный момент: сообщить тему урока, сформулировать цели урока.

Проводится фронтальный опрос учащихся:

1. Какие функции называются возрастающими (убывающими)?
2. Какие функции называются монотонными?
3. Какие свойства монотонных функций вы знаете?

Свойство 1. Если y=g(x) – монотонно возрастает на промежутке I и y=f(x) – монотонно возрастает на промежутке I, то y=g(x)+f(x) – монотонно возрастает на промежутке I.

Свойство 2. Если y=f(x) возрастает (убывает) на промежутке I, то уравнение f(x)=a имеет на I не более одного корня.

Свойство 3. Если y=f(x) возрастает на I, а y=g(x) убывает на I, то уравнение f(x)=g(x), имеет не более одного корня.

II. Решение уравнений

( Этот этап урока проходит в форме беседы учителя с учениками. Ученики, основываясь на прошлом опыте решения уравнений, предлагают свои решения. Учитель показывает им более рациональные способы решения этих уравнений)

Пример 1. Решите уравнение: x 5 +x 3 +2x-4=0.

Решение: Функция f(x)=x 5 +x 3 +2x-4 возрастает как сумма трех возрастающих функций y=x 5 , y=x 3 и y=2x-4 на R.

Тогда уравнение f(x)=0 имеет не более одного корня. Испытывая делители свободного члена, находим, что x=1.

Пример 2. Решите уравнение .

Решение: Функция — возрастает на своей области определения, как сумма двух возрастающих функций и . Следовательно, уравнение f(x)=2 имеет не больше одного корня на [-1,45; 26]. Непосредственно проверкой убеждаемся что f(1)=0. Уравнение решено: мы нашли корень и доказали, что других корней нет.

Учащимся предлагается решить это уравнение дома с помощью возведения в квадрат лавой и правой частей уравнения, и убедится что решение будет очень громоздким.

Пример 3. Решите уравнение log₂(x+2)=1-x.

Решение: Функция y=log₂(x+2) – возрастает на (-2; +). Функция y=1-x убывает на R. Тогда уравнение log₂(x+2)=1-x имеет единственное решение при x (-2; +).

Непосредственно проверкой убедимся, что x=0 является корнем этого уравнения.

Каким еще способом можно решить это уравнение? (графически)

Пример 4. Определите число корней уравнения .

Решение: Рассмотрим функцию эта функция возрастает на области определения , тогда , т.е. f(x)4, где x D(f). Значит множеством значений функции f(x) является промежуток [+4;+).

Т.е. при a4 уравнение имеет единственное решение, при a 5 +3x=4.

Решить уравнение .

II. Вариант:

Решить уравнение x 5 +7x=-8.

Решить уравнение .

1. Решить уравнение .

IV. К доске приглашаются ученики из обоих вариантов и показывают решение уравнений

V. Подведение итогов урока и выставление оценок

VI. Задание на дом

1. Определить число корней уравнения .
2. Решить уравнение x 5 +2x 3 +3=54.

[1] В.В. Локоть. Применение свойств функций, преобразование неравенств // АРКТИ, Москва 2007 г.

[2] Ю.Н. Макарычев. Дополнительные главы к школьному учебнику 9 класс // Просвещение, 1998 г.

[3] И.Я. Виленкин. Алгебра и математический анализ 10 // Просвещение, 1998 г.

[4] Е.Д. Кулакин. 3000 конкурсных задач по математике // Москва 2002 г.

Видео:Показательное уравнение // Применение монотонности функций для решения уравненийСкачать

Решение уравнений с помощью монотонности функций

Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).

Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.

1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.

Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.

Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.

Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.

Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.

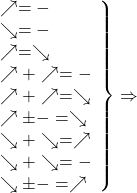
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:

то уравнение имеет единственный корень или не имеет корней.

Разумеется, количество слагаемых может быть больше двух.

Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):

1),y = x(a > 1),]» title=»Rendered by QuickLaTeX.com»/>

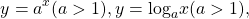
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:

1),y = — x(a > 1),]» title=»Rendered by QuickLaTeX.com»/>

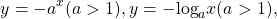
Примеры решения уравнений с помощью использования монотонности функций.

Перепишем уравнение в виде

является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

На промежутке (-∞;0) функция

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.

Аналогично, на промежутке (0:∞)

— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.

В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.

2 комментария

Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям

Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.

Видео:Три уравнения на одну идею. Используем монотонность функций Алгебра 10-11Скачать

Применение свойства монотонности функции в решении уравнений.

Презентация. Решение уравнений одним из нестандартных методов.

Видео:Монотонность функции | МатематикаСкачать

Скачать:

Предварительный просмотр:

Видео:Свойство монотонности в решении базовых уравненийСкачать

Подписи к слайдам:

Применение свойства монотонности функций в решении уравнений и неравенств

Введение При решении уравнений школьники часто сталкиваются с заданиями творческого характера. Часть из них можно решить, используя свойство монотонности.

Свойство Если y = f ( x ) монотонно возрастает на промежутке I и функция y = g ( x ) монотонно возрастает, то y = f ( x )+ g ( x ) монотонно возрастает на этом промежутке.

Рассмотрим уравнение: f ( x )= а Если f ( x ) монотонно возрастает на промежутке I , то она может принимать значение а не более чем в одной точке, т.е. данное уравнение имеет не более одного корня.

Например : х 5 +х 3 +2х=4 Левая часть данного уравнения монотонно возрастает. Значит уравнение имеет не более одного корня. При х=1, получим 1+1+2*1=4 4=4 х=1 единственный корень уравнения. Ответ: х=1

Рассмотрим уравнение: f ( x ) = g ( x ) Если функция f ( x ) монотонно возрастает на некотором промежутке I , а функция y = g ( x ) монотонно убывает, то кривые y = f ( x ) и y = g ( x ) на плоскости могут пересечься не более чем в одной точке, значит данное уравнение имеет не более одного корня.

Например: х+16=(1/15) х 1) Левая часть данного уравнения, функция возрастающая, как линейная с положительным угловым коэффициентом 2) Правая часть данного уравнении, функция убывающая, как показательная с основанием меньше единицы.

Значит, уравнение имеет не больше одного корня. При х = -1 имеем -1+16=(1/15) -1 Х = -1 единственный корень уравнения. Ответ: х=-1

Пример №1 4 x — x 2 =2 x 2 -4 x +6 -( x 2 -4 x )= 2 x 2 -4 x +6 Пусть x 2 -4 x = t , тогда — t=2t+6

Левая часть y = — t , убывающая на R . Правая часть y =2 t +6 показательная, возрастает на R .(2>1) t=-4 По скольку t = x 2-4 x , решим уравнение. Х 2 -4х+4=0 Х=2 Ответ: х=2.

Метод, основанный на перечисленных утверждениях, состоит в следующем: Выделить функции; Установить их монотонность; Подобрать корень уравнения; Обосновать на приведенное утверждение, что других корней нет; Записать ответ.

Условия монотонности. Монотонность функции связана с тем, каков знак ее производной: Если f’(x)>0 в каждой точке интервала I , то функция f возрастает на I . Если f’(x) 0? => f(x) возрастает на ( ∞;1/3 |

Следовательно, она принимает каждое свое значение только в одной точке. ___ Значит, уравнение x 5 +x 3 — √ 1-3x+4 имеет не более одного корня. При х=-1 , получим -1-1-2+4=0 0=0 Ответ: х = -1

Пример №2 xlog 3 x -(2 x +3) log 3 x +6=0. Решение Обозначим log 3 x = t . Приходим к квадратному относительно t уравнению xt 2 -(2х+3) t +6=0. его корни t 1,2 =((2х+3)±(2х-3)/2х t 1 =2, log 3 x = 2, х = 9 t 2 =3/х. log 3 x = 3/х.

при х>0 функция у = log 3 x — возрастающая, функция у = 3/х- убывающая. Поэтому, если существует корень уравнения log 3 x = 3/х, то он единственный. Подбором находим корень х = 3 Ответ: 3;9.

Заключение При использовании нестандартных методов, решение занимает меньше времени, а также оно более интересно.

📸 Видео

10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумыСкачать

Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Как решать сложные параметры с помощью монотонности?🔥 Все полезные методы😍Скачать

СВОЙСТВА ФУНКЦИИ — Промежутки Знакопостоянства и МонотонностиСкачать

Алгебра 10 класс. 11 сентября. Исследование функции на монотонность, используя свойства числовых нСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Промежутки монотонности функции.Скачать

монотонность функции решение уравненийСкачать

Мини-Лекция №5 Олимпиады OlimpWay по математике 2019 (Монотонность функции)Скачать

Параметр. Серия 5. Что такое монотонная функция и как с ее помощью решать задачиСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Алгебра 9 класс (Урок№3 - Свойства функций)Скачать

Математический анализ, 12 урок, Монотонность и экстремумы функцииСкачать

Алгебра 10 класс. 10 сентября. Исследование функции на монотонность, используя свойства числовых нСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать