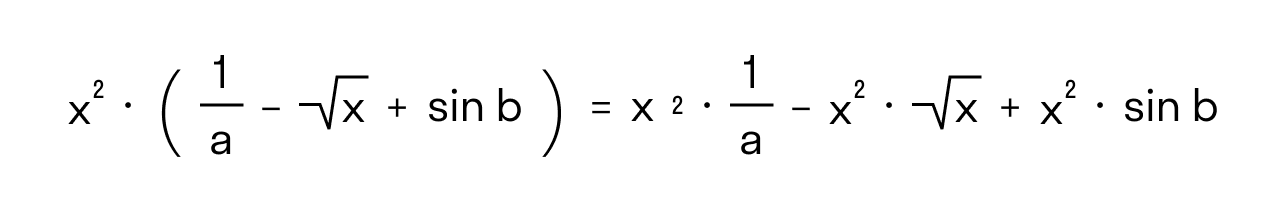Как решать уравнения 5 класс математика со скобками с минусом и плюсом

Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Памятка : «Решение уравнений», 5 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

(Х – 87) – 27 = 36; Х-87 в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

Х – 87 = 63; х в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

Проверка: (150 – 87) – 27 = 36;

87- ( 41 + У ) = 22; 41 + У в уравнении является вычитаемым . Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность

41 + У = 65; У в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое

Проверка: 87- ( 41 + 24 ) = 22;

(у – 35) + 12 = 32; у – 35 в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое

у – 35 = 20; у в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

(237 + х) – 583 = 149;

468 – ( 259 – х) = 382;

(237 + х) – 583 = 149;

237 + х = 149 + 583;

(237 + х) – 583 = 149;

237 + х – 583 = 149;

х – (583 – 237) = 149;

468 – ( 259 – х) = 382;

259 – х = 468 – 382;

468 – ( 259 – х) = 382; 468 – 259 + х = 382;

Решение уравнений, приведение подобных слагаемых

Пример 1: 8х-х=49 ; сначала запишем знаки умножения,

8*х-1*х=49 ; затем воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*7=49 ; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель

Пример 2: 2х+5х+350=700 ; воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*(2+5)+350=700 ; приведем подобные слагаемые (т.е. сложим числа в скобках)

7х является неизвестным слагаемым . Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

7х=350; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель

2*50 + 5*50 + 350 = 700;

100 + 250 + 350 = 700;

Пример: 270: х + 2 = 47;

( 270 : х — является слагаемым.

Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

( х является делителем . Чтобы найти неизвестный делитель , нужно делимое разделить на частное)

Пример: а : 5 – 12 = 23;

Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое )

( а является делимым. Чтобы найти неизвестное делимое , нужно частное умножить на делитель .

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 692 человека из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 862 человека из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 48 человек из 20 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 843 532 материала в базе

Материал подходит для УМК

«Математика», Виленкин Н.Я., Жохов В.И. и др.

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 09.12.2019
• 266
• 2

• 08.12.2019
• 261
• 0

• 19.11.2019
• 211
• 2

• 18.11.2019
• 957
• 7

• 18.11.2019
• 330
• 0

• 17.11.2019
• 329
• 0

• 17.11.2019
• 351
• 12

• 17.11.2019
• 237
• 6

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 15.12.2019 58557
• DOCX 17.4 кбайт
• 6538 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Кретинина Светлана Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 7 месяцев
• Подписчики: 0
• Всего просмотров: 63490
• Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Уравнения со скобками - 5 класс (примеры)Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минобрнауки отменило плановые и внеплановые проверки вузов в 2022 году

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

В Госдуме предложили унифицировать школьные программы

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Уравнение с двумя скобками.5 класс.МатематикаСкачать

Раскрытие скобок: правила и примеры

Раскрытие скобок и правила применения — это одна из основных тем математике, на базе которой решаются многие задания во всех последующих классах. Поэтому правила раскрытия скобок необходимо усвоить в обязательном порядке.

Итак, основная функция скобок – задать порядок вычислений, так как в зависимости от того, в какой последовательности будут решаться примеры и выражения, зависит ответ. Раскрыть скобки означает избавиться от них, не влияя на результат . При этом существуют правила, которые применяются при раскрытии скобок.

Видео:Уравнение. 5 класс.Скачать

Раскрытие скобок: правила

Правило раскрытия скобок при сложении

Если перед скобками стоит плюс, то скобки просто опускаются.
Иными словами, скобки исчезнут, а то, что было в скобках, запишется без изменений.
Например, (a−b) = a−b.

В данном правиле следует учитывать, что в математике не принято писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа 2 и 3, то запишем 2+3, а не +2+3. Значит перед скобками, которые стоят в начале выражения, стоит плюс, который не пишут.

Пример 1: 8+(5−3) = 10. Ответ: 8+5–3 = 10.
Пример 2: 6+(−1+2) = 7. Ответ: 6–1+2 = 7.
Пример 3: 8a + (3b −6a). Ответ: 8a + 3b −6a = 2a + 3b.

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то скобки опускаются, а каждое слагаемое внутри нее меняет свой знак на противоположный.
Например, −(a−b) = −a+b

Пример 1: 8–(5–3) = 6. Ответ: 8 – 5 + 3 = 6.
Пример 2: 6 − (−1 + 2) = 5. Ответ: 6 + 1 – 2 = 5.
Пример 3: 8a–(3b −6a). Ответ: 8a – 3b + 6a = 14a – 3b.
Пример 4: −(5b −2). Ответ: −5b +2.

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число внутри скобок умножается на множитель, стоящий перед скобками.
При этом умножение минуса на минус дает плюс, а умножение минуса на плюс дает минус.
Данное правило основано на распределительном законе умножения: a(b+c) = ab + ac.

Пример 1: 8×(5 − 3) = 16. Ответ: 8 ×5 − 8 ×3 = 16.
Пример 2: a×(7 +2). Ответ: a×7+a×2 = 7a + 2a = 9a.
Пример 3: 8×(3b −6a). Ответ: 8×3b – 8×6a = 24b–48a

Раскрытие скобок при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок.

Пример 1: (25−15):5. Ответ: 25:5−15:5= 2.
Пример 2: (−14a +10):2. Ответ: −14a:2 +10:2 = −7a +5.
Пример 3: (36b + 6a):6. Ответ: 36b:6 + 6a:6 = 6b + a.

Раскрытие скобок при умножении двух скобок

При умножении скобки на скобку, каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.
Например, (c+d) × (a−b) = c×(a−b)+d×(a−b) = ca−cb+da−db

Пример. Раскрыть скобки: (2−a) × (3a−1).
Решение:
Шаг 1. Убираем первую скобку (каждое ее слагаемое умножаем на вторую скобку): 2 × (3a−1) − a × (3a−1).
Шаг 2. Раскрываем произведение скобок: (2×3a− 2×1) – (a×3a−a×1) = 2×3a− 2×1 – a×3a + a×1.
Шаг 3. Перемножаем и приводим подобные слагаемые: 6a–2–3a2+a = 7a–2–3a2

Раскрытие вложенных скобок

Иногда встречаются примеры со скобками, которые вложены в другие скобки. Чтобы решить такую задачу, нужно сначала раскрыть внутреннюю скобку (при этом остальное выражение оставить без изменений), а потом внешнюю скобку.

Пример 1. 7a + 2 × (5− (3a+b)).
Решение:
Шаг 1. Раскроем внутреннюю скобку (не трогая остальное): 7a + 2 × (5 − (3a+b)) = 7a + 2 × (5 − 3a − b).
Шаг 2. Раскроем внешнюю скобку: 7a + 2 × (5 − (3a+b)) = 7a + 2×5 − 2×3a − 2×b.
Шаг 3. Упростим выражение: 7a + 10 − 6a − 2b = a+10-2b.

Раскрытие скобок в натуральной степени

Если стоит скобка в натуральной степени (n), то чтобы раскрыть скобки, нужно найти произведение скобок, перемноженных несколько раз (n раз).

Например, в примере (a+b)2 = (a+b)×(a+b) нужно перемножить скобки (a+b) два раза, далее раскрываем скобки, где каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Раскрытие скобок

О чем эта статья:

Видео:Уравнения. 5 классСкачать

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

• знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
• произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

• 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1

Видео:УРАВНЕНИЯ СО СКОБКАМИ. Примеры | МАТЕМАТИКА 5 классСкачать

Первое правило раскрытия скобок

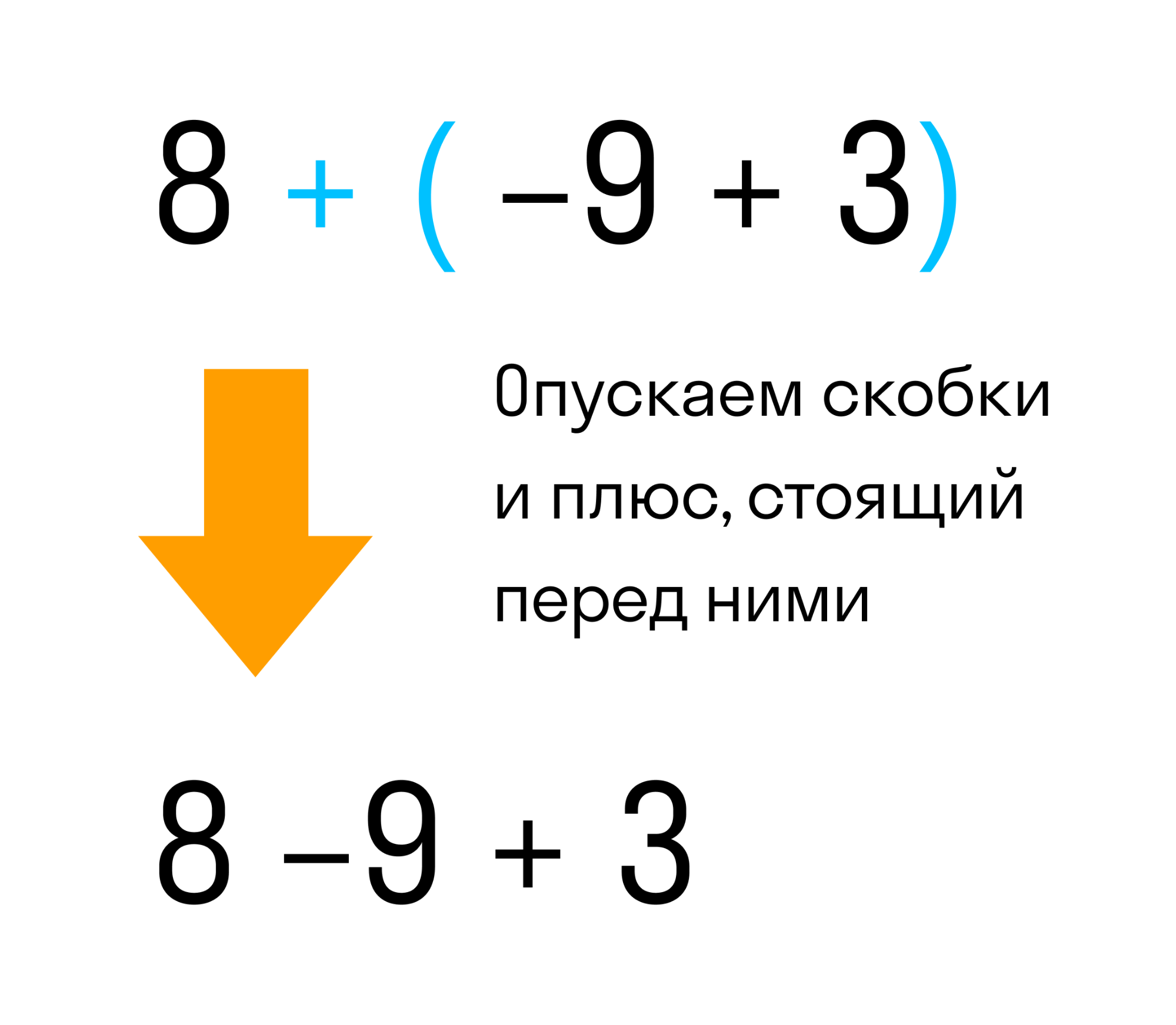
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

• 2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

• 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

• 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Как решать #уравнения, что делать если перед скобкой #минус, как открыть скобку в уравнении #5классСкачать

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

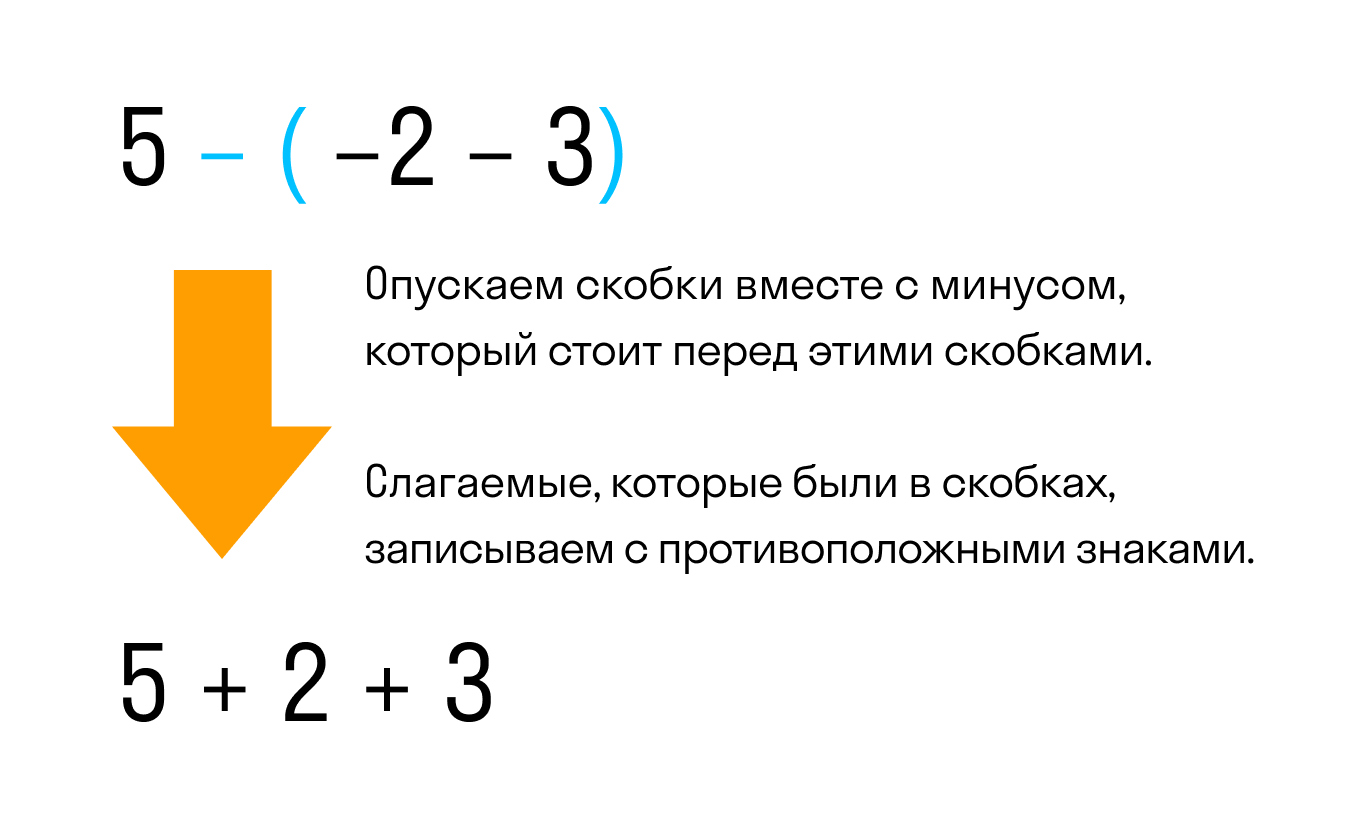
Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

18 − (−1 − 5) = 18 + 1 + 5

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Видео:Решение уравнений. Как решать уравнения - 5 классСкачать

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

(a + b) : c = a/c + b/c.

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

• (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Видео:Уравнение 5 классСкачать

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

• перед скобкой стоит знак плюс:

a + (b — c + d) = a + b — c + d

• выражение начинается со скобки и перед ней нет знака:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

• перед скобкой стоит знак минус:

a — (b — c + d) = a — b + c — d

• выражение начинается с минуса перед скобкой:

-(a + b — c) + d = -a — b + c + d

Раскрытие круглых скобок при умножении одночлена на многочлен

a + b(c + d — f + e) = a + bc + bd — bf + be

a + b(c + d — f + e) = a + bc + bd — bf + be

-a(b + c — d) + f = -ab — ac + ad + f

Раскрытие круглых скобок при умножении многочлена на многочлен

(a + b)(c — d) = a(c — d) + b(c — d) = ac — ad + bc — bd

(-a + b)(c + d) = -a(c + d) + b(c + d)= -ac — ad + bc + bd

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Видео:11. Уравнения (Виленкин, 5 класс)Скачать

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

• упростить выражение 7x + 2(5 − (3 x + y)).

Чтобы успешно решать подобные задания, нужно:

• внимательно разобраться со скобками — какая в какой находится.
• раскрывать скобки последовательно, начиная с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y).

Теперь раскроем вторую скобку, внешнюю:

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y.

Упростим получившееся выражение:

• 7x + 2(5 − (3x + y)) = 7x + 2(5 − 3 x − y) = 7 x + 2 * 5 − 2 * 3 x − 2 * y = 7x + 10 − 6x − 2y.

• 7x + 10 − 6x − 2y = x + 10 − 2y

Видео:Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

• возвести многочлены в скобках в натуральную степень;
• слева направо провести умножение и деление;
• когда в скобках останутся только слагаемые, раскрыть скобки и привести подобные.

Пример 1. Раскрыть скобки и упростить выражение:

-(2a + 5b) + (3a — 2b + 1) — (2a + 4) = -2a — 5b + 3a — 2b + 1 — 2a — 4 = (-2a + 3a — 2a) + (-5b — 2b) + (1 — 4) = -a — 7b — 3

Пример 2. Доказать, что при любых значениях переменной a значение выражения 3(2a — 7) — (a + (5a — 4)) — отрицательно.

33(2a — 7) — (a + (5a — 4)) = 3(2a — 7 ) — (a + 5a — 4)= 6a — 21 — a — 5a + 4 = (6a — a — 5a) + (-21 + 4) = -16/p>

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Видео:Уравнение. Практическая часть - решение задачи. 2 часть. 5 класс.Скачать

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 1. Раскройте скобки в выражении: 2 + (6 + 3) + 2 — (1 + 1)

Задание 2. Раскройте скобки в выражении: — 21 + 14 + (-1 + 5) — 11 + ( 3 + 2)

Задание 3. Раскройте скобки в выражении: 3 * (-4m + 3n — 5)

Задание 4. Раскройте скобки в выражении: -(12a — 5b — 2)

Задание 5. Раскройте скобки в выражении: 3(x — 9)

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

🔥 Видео

Правила решения уравнений в 5 классе. Как запомнить и вывести их самому.Скачать

Решение сложных уравнений 4-5 класс.Скачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

КАК РАСКРЫТЬ СКОБКИ?Скачать

Обыкновенные дроби и действия над ними. Практическая часть. 5 класс.Скачать

Решение уравнений (относительно сложения и вычитания) 5 классСкачать