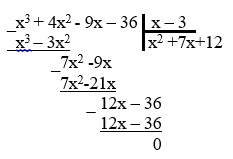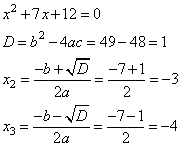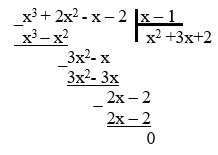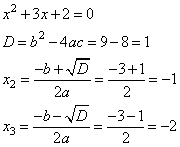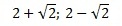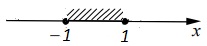В данном задании необходимо решить уравнение степени больше двух — это может быть биквадратное или кубическое уравнение. Ниже мы приводим алгоритмы решения типовых заданий.
Алгоритм решения:
- Определить тип уравнения.
- Перенести правую часть уравнения в левую.
- Привести уравнение к виду, при котором можно его многочлен слева разложить на множители.
- Разложить на множители.
- Приравнять каждый множитель к нулю
- Решить полученные уравнения.
- Записать ответ.
Решение:
1. Уравнение четвертой степени.
2. Перенесем правую часть уравнения в левую:
x 4 – (4x – 5) 2 = 0
3. Уравнение уже приведено к виду, при котором можно его левую часть разложить на множители.
4. Данное уравнение разложим на множители по формуле разности квадратов. Получим:
(х 2 – (4х-5))( х 2 + (4х-5)) = 0, или (х 2 – 4х+5)(х 2 + 4х-5) = 0.
5. Приравняем каждый множитель к нулю:
х 2 – 4х+5 = 0 и х 2 + 4х-5 = 0
6. Решим каждое из уравнений по формулам дискриминанта и корней:
Для первого уравнения:
D = b 2 -4ac = 16-20 = – 4, это означает, что первое уравнение х 2 – 4х+5 = 0 не имеет корней.
Для второго уравнения:
Определим корни второго уравнения:
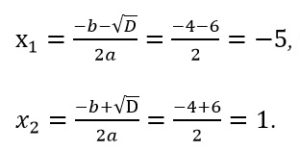
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решение:
1. Перед нами уравнение третьей степени общего типа.
2. Найдем делители свободного члена данного уравнения. Это числа: 1; -1; 2; -2; 3; -3; 4; -4; 6; -6; 12; -12;.18; -18; 36; -36.
3. Рассмотрим числа 1; -1; 2; -2; 3; -3. Это наименьшие среди найденных делителей. Подставим их по очереди в уравнение вместо х:
- для x=1:
– не подходит;
- для x=-1:
– не подходит;
- для х=2: 2 3 +4∙2 2 -9∙2=8=16-18-36=-38≠0 – не подходит;
- для х=-2: (-2) 3 +4∙(-2) 2 -9∙(-2)-36=-8+16+18-36=-10≠0 – не подходит;
- для x=3:
– подходит.
Мы нашли один корень.
4. Теперь выполним деление кубического многочлена на x-3, воспользовавшись схемой Горнера, имеем:
| 1 | 4 | -9 | -36 | |
| 3 | 1 | 7 | 12 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. После деления получаем квадратный трехчлен:
Составим квадратное уравнение для вычисления оставшихся двух корней:
6. Решим его с помощью формул корней и дискриминанта
7. Получили три корня 3; -3; -4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
– для x=1: 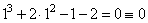
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
| 1 | 2 | -1 | -2 | |
| 1 | 1 | 3 | 2 | 0 |
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
5. Получаем квадратный трехчлен
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
7. Получили три корня -2; -1; 1.
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Решение:
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
Возвращаемся к переменной х. Поскольку (х–2) 2 =а, то получим:
это уравнение корней не имеет, т.к. нельзя извлечь
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Корни уравнения:
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Используя формулу сокращенного умножения для квадрата разности, раскрываем скобки в левой и правой части неравенства.
- Группируем элементы (слагаемые) неравенства: слагаемые с «х» должны оказаться в левой части, свободные члены – в правой. Приводим подобные.
- Решаем полученное неравенство.
Решение:
х≤|1| → –1≤x≤1 → xϵ[–1; 1]
pазбирался: Даниил Романович | обсудить разбор | оценить
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном уравнении с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х 2 на а. Решаем полученное квадратное уравнение.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у: 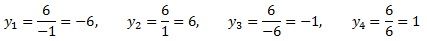
pазбирался: Даниил Романович | обсудить разбор | оценить
Нам дано уравнение третьей степени: х 3 + 6х 2 =4х + 24
В данном уравнении перенесем все слагаемые в одну сторону ( в левую), изменяя при этом знаки: х 3 + 6х 2 – 4х – 24=0
Теперь сгруппируем слагаемые: (х 3 + 6х 2 ) – (4х + 24)=0
Вынесем общий множитель за скобки из каждой группы: х 2 (х + 6) – 4(х + 6)=0
Вынесем за скобки выражение (х + 6): (х + 6)(х 2 – 4)=0
Приравняем каждый множитель к нулю и решим полученные уравнения:
х + 6=0 и х 2 – 4=0
х=6 х 2 =4, отсюда х1,2= ± 2
pазбирался: Даниил Романович | обсудить разбор | оценить
Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби:
4 a − 9 b + 3 9 a − 4 b + 3 . . = 5
5(9а – 4b + 3)=4a – 9b+3
Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные): 45a – 20b +15 =4a – 9b+3 45a – 20b – 4a + 9b=3 – 15 Приведем подобные слагаемые: 41a – 11b = – 12 Выпишем выражение, значение которого надо найти: 41a – 11b + 15 и заменим в нем 41a – 11b на число -12, полученное при упрощении нашей дроби: 41 a – 11 b + 15= – 12 + 15=3. Видим, что значение нашего выражения получилось равным 3.Ответ: 3
pазбирался: Даниил Романович | обсудить разбор | оценить
Данное уравнение является квадратным. Но в его условии присутствует квадратный
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Решаем полученное неравенство: − х ≥ − 5 , отсюда х ≤ 5 . Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х 2 − 2 х + √ 5 − х − √ 5 − х − 24 = 0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х 2 − 2 х − 24 = 0
Итак, корнями уравнения х 2 − 2 х − 24 = 0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 н е ≤ 5 , а число минус 4 записываем в ответ нашего уравнения, так как − 4 ≤ 5 .
pазбирался: Даниил Романович | обсудить разбор | оценить
Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:
У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:
Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел ( 0 )
Для этого найдем нули функции, решая с помощью дискриминанта:
Д=(-4) 2 – 4 ∙ 1 ∙ 1 =16-4=12
х 1 = 4 − √ 12 2 . . = 2 ( 2 − √ 3 ) 2 . . = 2 − √ 3
Знаем, что х2 будет отличаться только знаком, получим, что х 2 = 2 + √ 3 Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки ( 2 − √ 3 ) до точки ( 2 + √ 3 ) . 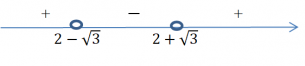
pазбирался: Даниил Романович | обсудить разбор | оценить
Чтобы решить данное задание, необходимо понимать, что выполнять действия умножение и деление степеней мы можем в том случае, если они имеют одинаковые основания. Поэтому разложим на множители основание 36 нашего числителя так, чтобы вместо 36 были числа 4 и 3, которые есть в знаменателе.
( 3 ∙ 3 ∙ 4 ) n 4 n − 2 ∙ 3 2 n − 1 . .
Теперь представим каждый множитель в виде степени:
3 n ∙ 3 n ∙ 4 n 4 n − 2 ∙ 3 2 n − 1 . .
Разложим знаменатель дроби на множители по свойству степеней
3 n ∙ 3 n ∙ 4 n 4 n ∙ 4 − 2 ∙ 3 2 n ∙ 3 − 1 . .
Теперь можно сократить числитель и знаменатель на 3 n и в 4 n степени
Получим дробь, которую преобразуем по свойству степеней:
. . 1 4 − 2 ∙ 3 − 1 . . = 4 2 ∙ 3 1 1 . . = 16 ∙ 3 = 48
pазбирался: Даниил Романович | обсудить разбор | оценить
Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:
( х − 5 ) 2 − √ 7 ( х − 5 ) 0 Теперь вынесем за скобки общий множитель (х-5), получим: ( х − 5 ) ( х − 5 − √ 7 ) 0 Найдем нули функции, приравнивая каждый множитель к нулю: х − 5 = 0 , откуда х=5 х − 5 − √ 7 = 0 , откуда: х = 5 + √ 7 Отметим эти числа на числовом луче и найдем интервал отрицательных чисел: 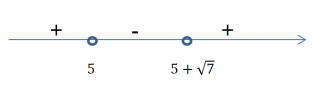
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Разбор задания 20 ОГЭ-2019 по математике
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Видео:Задание №20. Уравнение 2 часть ОГЭ по математике 2023 | УмскулСкачать

Часть 1
Задание 20
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.
Решение
Первое утверждение есть аксиома параллельных прямых. Второе утверждение неверно, так как для отрезков с длинами 1, 2, 4 не выполняется неравенство треугольника (сумма длин любых двух сторон меньше длины третьей стороны)
Третье утверждение верно – в параллелограмме противолежащие углы равны.
Видео:Все типы 20 задания ОГЭ по математике | Молодой репетиторСкачать

Подготовка к решению №20 ОГЭ по математике
Разделы: Математика
Класс: 9
Ключевые слова: геометрия , ГИА
Современное общество понимает важность математического образования подрастающего поколения, признает его необходимость. Математика является обязательным предметом на всех этапах школьного обучения с 1 по 11 класс, экзамен по математике является обязательным в 9 и 11 классах. В настоящее время в рамках ОГЭ по математике проводится проверка знаний и по алгебре, и по геометрии. Задачи по геометрии занимают примерно третью часть всех заданий КИМов. Задания базового уровня направлены на проверку знаний основных фактов курса геометрии, умения решать простейшие задачи.
Как помочь каждому школьнику справиться заданиями ГИА, а учителю эффективнее организовать учебный процесс? Не секрет, что прочными математическими знаниями обладают единицы.
Геометрия как учебный предмет играет огромную роль в развитии познавательной активности и любознательности, логического мышления и пространственного воображения учащихся, формирует не только специальные геометрические знания учащихся, но и влияет на общее развитие личности, умение логически мыслить, доказательно обосновывать утверждения в любой сфере деятельности. Каждый учитель старается вернуть интерес к предмету, показать его значимость в различных сферах человеческой деятельности, научить ученика учиться и применять накопленные знания в практической деятельности.
В процессе обучения геометрии важное место занимает проверка теоретических знаний. Необходимость повторения – это требования одной из задач обучения, требующая прочного и сознательного овладения знаниями. Повторение материала осуществляется во всей системе учебного процесса. Формы и виды повторения могут быть разнообразными. Одна из форм повторения – обобщающее повторение. Обобщающее повторение дает возможность осуществлять дифференцируемый подход к учащимся, учитывать их возрастные и индивидуальные особенности, учитывать особенности класса, умения и навыки учащихся.
Учитель сам определяет, что повторять, как повторять и когда повторять, стремясь привести в систему знания и умения учащихся, устранить пробелы в знаниях учащихся, обобщить, систематизировать и окончательно закрепить наиболее существенное из учебного материала.
В своей работе я использую различные методы повторения, в том числе и метод обобщающего повторения, который, как я считаю, является более эффективным при подготовке к ОГЭ учащихся 9 класса. Повторение по геометрии строю на повторении определений, свойств основных геометрических фигур – треугольников, четырехугольников, многоугольников, окружности и круга.
Умение применять теоретические знания при решении задач говорит о большой эффективности такого повторения. Обобщающее повторение способствует повышению качества знаний учащихся.
В течение учебного года по окончании четверти с учащимися провожу зачеты по формулировкам теорем и определений по образцу задания №20 ОГЭ. По окончании года все формулировки собираю воедино и провожу зачет по всему материалу прошедшего учебного года.
В данной работе представлены карточки с формулировками, в которых нужно выбрать верные или неверные утверждения. Каждый ученик на зачете получает не менее 10 карточек. Ему нужно заполнить бланк для заполнения результатов (Приложение 1). Получением зачета является успешное выполнение 9-10 карточек. Для быстрого получения результата зачета для себя готовлю таблицу с правильными ответами (Приложение 2).
Я готовлю к ГИА учащихся много лет. Мой опыт позволяет сделать вывод, что такая форма работы способствует успешной подготовке к сдаче учащимися ГИА.
Карточка 1 (верные/ неверные)
- Сумма длин всех сторон называется площадью многоугольника
- Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности
- Диагонали ромба взаимно перпендикулярны и делят его углы пополам
- Около четырехугольника всегда можно описать окружность
Карточка 2 (верные/ неверные)
- Отрезок, соединяющий любые две соседние вершины, называется диагональю многоугольника
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания
- Квадратом называется прямоугольник, у которого все стороны равны
- Около треугольника нельзя описать окружность
Карточка 3 (верные/ неверные)
- Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины
- Катет прямоугольного треугольника есть среднее арифметическое для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла
- Два угла квадрата острые, а два другие — прямые
- Около любого треугольника можно описать окружность
Карточка 4 (верные/ неверные)
- Сумма углов невыпуклого n-угольника равна (n-2)×180°
- Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой
- Диагонали квадрата не равны
- Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность
Карточка 5 (верные/ неверные)
- Две смежные стороны четырехугольника называются противоположными
- Медианы треугольника пересекаются в одной точке, которая делит его медиану в отношении 2:1, считая от вершины
- Равные многоугольники имеют равные периметры
- В любом описанном четырехугольнике суммы противоположных сторон равны
Карточка 6 (верные/ неверные)
- Сумма углов выпуклого четырехугольника равна 180°
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна произведению площадей этих многоугольников
- Не во всякий четырехугольник можно вписать окружность
Карточка 7 (верные/ неверные)
- Параллелограммом называется квадрат, у которого противоположные стороны попарно параллельны
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны
- Площадь квадрата равна сумме его сторон
- В треугольник можно вписать только одну окружность
Карточка 8 (верные/ неверные)
- В параллелограмме противоположные стороны равны, а противоположные углы — не равны
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
- Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
- Не в любой треугольник можно вписать окружность
Карточка 9 (верные/ неверные)
- Диагонали параллелограмма точкой пересечения делятся пополам
- Если два угла одного треугольника соответственно равны двум сторонам другого, то такие треугольники подобны
- Число k, равное произведению сходственных сторон подобных треугольников, называется коэффициентом подобия
- Высоты треугольника (или их продолжения) пересекаются в одной точке
Карточка 10 (верные/ неверные)
- Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – трапеция
- Отношение периметров двух подобных треугольников равно квадрату коэффициента подобия
- Средней линией треугольника называется отрезок, соединяющий середины двух его сторон
- Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке
Карточка 11 (верные/ неверные)
- Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
- Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник равнобедренный
- Синусом острого угла тупоугольного треугольника называется отношение противолежащего катета к гипотенузе
- Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему
Карточка 12 (верные/ неверные)
- Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
- В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
- Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка
Карточка 13 (верные/ неверные)
- Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – не параллельны
- Площадь трапеции равна произведению суммы ее оснований на высоту
- Тангенсом прямого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету
- Биссектрисы треугольника пересекаются в одной точке
Карточка 14 (верные/ неверные)
- Параллельные стороны трапеции называются боковыми, а не параллельные – основаниями
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общие точки
- Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе
Карточка 15 (верные/ неверные)
- Трапеция называется равнобедренной, если ее боковые стороны параллельны
- Если высоты двух треугольников равны, то их площади относятся как основания
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку
- Каждая точка биссектрисы неразвернутого угла равноудалена от его углов
Карточка 16 (верные/ неверные)
- Трапеция, один из углов которой прямой, называется прямоугольной
- Площадь прямоугольного треугольника равна половине произведения его катета и гипотенузы
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек
- Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно сумме отрезков другой хорды
Карточка 17 (верные/ неверные)
- Прямоугольником называется параллелограмм, у которого все углы прямые
- Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию
- Прямая, имеющая с окружностью две общие точки, называется касательной к окружности, а их общие точки называются точками касания прямой и окружности
- Центральный угол, опирающийся на полуокружность – прямой
Карточка 18 (верные/ неверные)
- Диагонали прямоугольника равны
- Площадь параллелограмма равна половине произведения его основания на высоту, проведенной к этому основанию
- Угол с вершиной в центре окружности называется ее вписанным углом
- Вписанные углы, опирающиеся на одну и ту же дугу, равны
Карточка 19 (верные/ неверные)
- Если в параллелограмме диагонали равны, то этот параллелограмм-ромб
- Площадь прямоугольника равна произведению его противоположных сторон
- Сумма градусных мер дуг окружности с общими концами равна 360°
- Вписанный угол измеряется половиной дуги, на которую он опирается
Карточка 20 (верные/ неверные)
- Ромбом называется пятиугольник, у которого все стороны равны
- Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки
- Угол, вершина которого лежит на окружности, а сторонами являются диаметры, называется вписанным углом
- Если прямая проходит через конец касательной, лежащей на окружности, и перпендикулярна к этому радиусу, то она является касательной
💡 Видео
Как решить систему уравнений на ОГЭ 2021? / Полный разбор задачи №20 ОГЭ по математикеСкачать

ОГЭ Задание 20 Разные способы решения систем уравненийСкачать

Задание 20 ОГЭ математика 2024 2 часть. Кубические уравненияСкачать

Задание №9 на ОГЭ. Как решать уравнения? Какие типы будут?Скачать

5 основных заданий из №20 из ОГЭ | Математика | TutorOnlineСкачать

ОГЭ. ЗАДАНИЕ 20. УРАВНЕНИЯСкачать

Задание №20. Экзамен ОГЭ. Система уравнений #shortsСкачать

ОГЭ 2023. Задание 20. Два способа решенияСкачать

Задание 20: ОВР с нуля | Поймет каждый | Химия ОГЭ | УмскулСкачать

Как решать 20 задание на ОГЭ 2023 по математике? / Все виды систем, которые могут вам встретитьсяСкачать

ОГЭ. НЕРАВЕНСТВА N-20, ЧАСТЬ-2Скачать

20 задание ОГЭ по математикеСкачать

Задание №20 на ОГЭ по химииСкачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

ОГЭ. Задание 20. ОВРСкачать

ОГЭ. ЗАДАНИЕ 20. СИСТЕМЫ УРАВНЕНИЙСкачать

20 задание ОГЭ по математикеСкачать

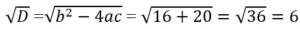
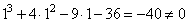 – не подходит;
– не подходит;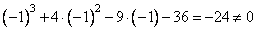 – не подходит;
– не подходит;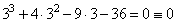 – подходит.
– подходит.