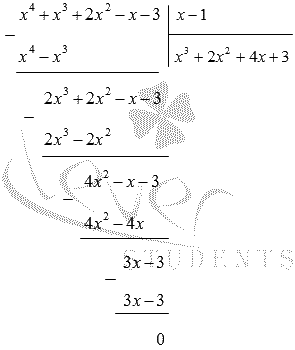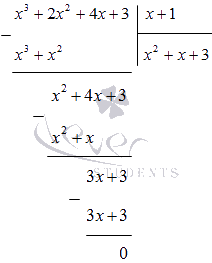Как решать уравнение с многочленами и степенями

Видео:Уравнение четвертой степениСкачать

Решение уравнений высших степеней

В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.

Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.

Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Уравнения высшей степени с целыми коэффициентами

Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :

a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0

Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .

Видео:7 класс// АЛГЕБРА // Умножение одночлена на многочлен, решение уравненийСкачать

Схема решения уравнения

Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .

Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .

Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.

Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.

У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.

Покажем на конкретном примере, как применяется такая схема решения.

Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .

Решение

Начнем с нахождений целых корней.

У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.

При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.

Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:

Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .

Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :

1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0

У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .

Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:

x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )

Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :

— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0

Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.

Оставшиеся корни будут корнями выражения x 2 + x + 3 .

D = 1 2 — 4 · 1 · 3 = — 11 0

Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .

Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.

В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .

После нахождения следующего корня, равного — 1 , мы получаем следующее:

Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.

Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .

Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .

Решение

У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .

Проверяем их по порядку:

1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0

Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:

В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .

Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.

2 3 + 2 2 — 3 · 2 — 6 = 0

Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :

В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .

Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.

Решим квадратное уравнение:

x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0

Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .

Ответ: x = — 3 2 ± i 3 2 .

Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.

Решение

x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0

Выполняем домножение 2 3 обеих частей уравнения:

2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0

Заменяем переменные y = 2 x :

2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0

В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .

Ответ: x 1 = — 1 , x 2 = 3 2

Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.

Видео:Решить уравнения, используя формулы сокращенного умножения.Сумма и квадрат разности. Алгебра 7 классСкачать

«Решение уравнений высших степеней». 9-й класс

Разделы: Математика

Класс: 9

Учебная:

Развивающая:

1. Развитие внимания учащихся.
2. Развитие умения добиваться результатов труда.
3. Развитие интереса к изучению алгебры и навыков самостоятельной работы.

Воспитывающая:

Оборудование: компьютер, проектор.

1 этап работы. Организационный момент.

2 этап работы. Мотивация и выход на постановку проблемы

Уравнение одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.

В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.

А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.

3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.

1) Решение линейного уравнения.

Линейным называется уравнение вида , где по определению. Такое уравнение имеет единственный корень .

2) Решение квадратного уравнения.

Квадратным называется уравнение вида , где . Количество корней и сами корни определяются дискриминантом уравнения . Для уравнение корней не имеет, для имеет один корень (два одинаковых корня)

, для имеет два различных корня .

Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение -й степени имеет не более n корней. Что касается самих корней, то тут ситуация намного сложнее. Для уравнений третьей и четвёртой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена на множители или с использованием замены переменной.

3) Решение кубического уравнения.

Решим кубическое уравнение

Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:

Итак, данное кубическое уравнение имеет три корня: ; ;.

4) Решение биквадратного уравнения.

Очень распространены биквадратные уравнения, которые имеют вид (т.е. уравнения, квадратные относительно ). Для их решения вводят новую переменную .

Решим биквадратное уравнение .

Введём новую переменную и получим квадратное уравнение , корнями которого являются числа и 4.

Вернёмся к старой переменной и получим два простейших квадратных уравнения:

(корни и )

(корни и )

Итак, данное биквадратное уравнение имеет четыре корня:

; ;.

Попробуем решить уравнение используя выше изложенные приёмы.

4 этап работы. Привести некоторые утверждения о корнях многочлена вида , где многочлен n-й степени

Приведём некоторые утверждения о корнях многочлена вида :

1) Многочлен -й степени имеет не более корней (с учётом их кратностей). Например, многочлен третьей степени не может иметь четыре корня.

2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.

3) Если на концах отрезка значения многочлена имеют разные знаки (т.е. ,), то на интервале находится хотя бы один корень. Это утверждение широко используется для приближенного вычисления корней многочлена.

4) Если число является корнем многочлена вида , то этот многочлен можно представить в виде произведения , где многочлен (-й степени. Другими словами, многочлена вида можно разделить без остатка на двучлен . Это позволяет уравнение -й степени сводить к уравнению (-й степени (понижать степень уравнения).

5) Если уравнение со всеми целыми коэффициентами (причём свободный член ) имеет целый корень , то этот корень является делителем свободного члена . Такое утверждение позволяет подобрать целый корень многочлена (если он есть).

5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.

Пример 1. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: . Проверка показывает, что корнем уравнения является число -1. Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы фактически разложили левую часть уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:

Итак, данное уравнение имеет три корня:

Пример 2. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть уравнения на множители:

Аналогичным образом поступим и с многочленом .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9), т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде

произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть исходного уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:

Итак, данное уравнение имеет четыре корня:

6 этап работы. Закрепление изученного материала.

Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.

7 этап работы. Вывод урока.

Решить уравнения высших степеней можно следующим образом:

• используя формулы для нахождения корней (если они известны);
• используя замену переменной;
• раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.

8 этап работы. Домашнее задание.

Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).

Видео:✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

Показательные уравнения

О чем эта статья:

6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:РЕШЕНИЕ УРАВНЕНИЯ С МНОГОЧЛЕНАМИ. Примеры | АЛГЕБРА 7 классСкачать

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.

Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.

🔥 Видео

11 класс, 3 урок, Уравнения высших степенейСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Вспоминаем схему Горнера и уравнения высших степенейСкачать

Сложение и вычитание многочленов. Алгебра, 7 классСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Многочлены. 7 класс.Скачать

7 класс, 21 урок, Сложение и вычитание многочленовСкачать

Произведение одночлена и многочлена. Умножение одночлена и многочлена. 7 класс.Скачать

Схема Горнера. 10 класс.Скачать

Теорема БезуСкачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

7 класс, 28 урок, Вынесение общего множителя за скобкиСкачать