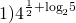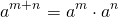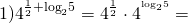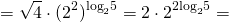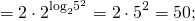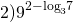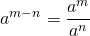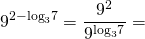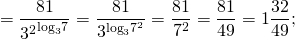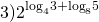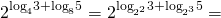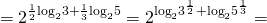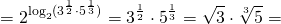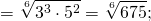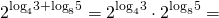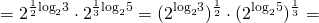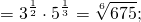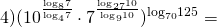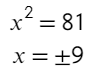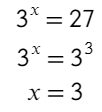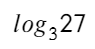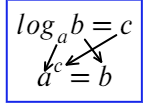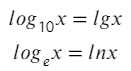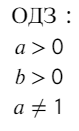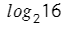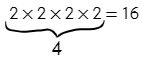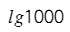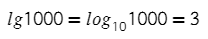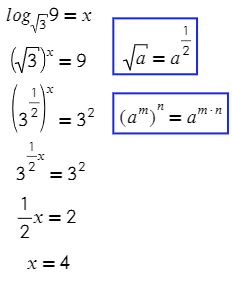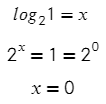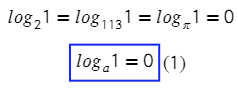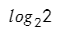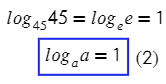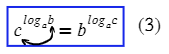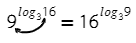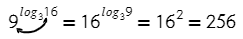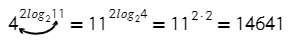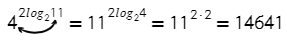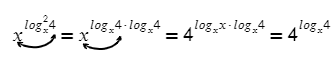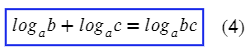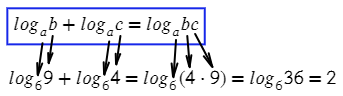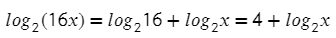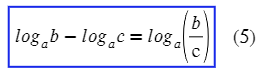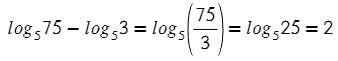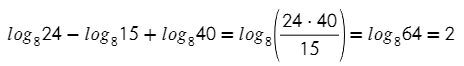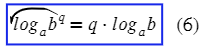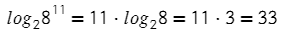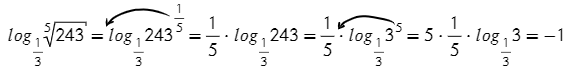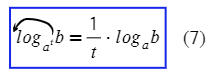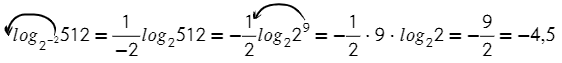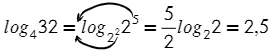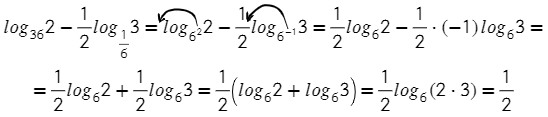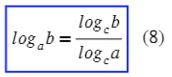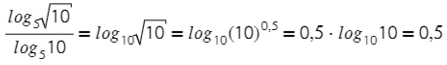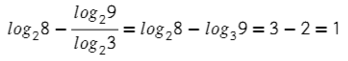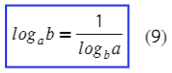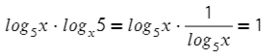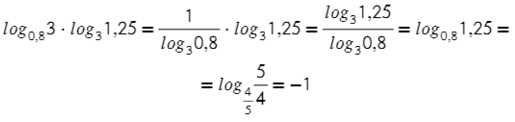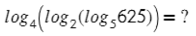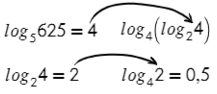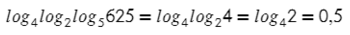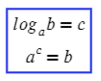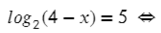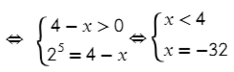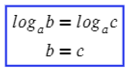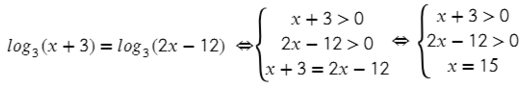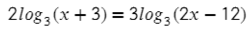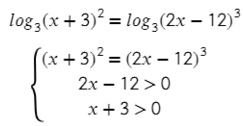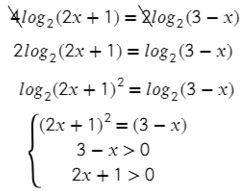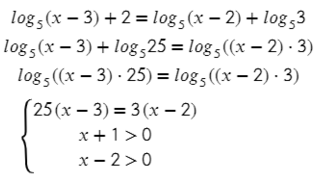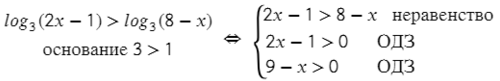Видео:Логарифм в степени - что с ним делать?Скачать
Логарифмические уравнения
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
При этом 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Обратим внимание на область допустимых значений логарифма:
Основное логарифмическое тождество:
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при 0,;a> 0,;aneq 1′ alt=’b> 0,;a> 0,;aneq 1′ />.
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
4. Решите уравнение:
Область допустимых значений: 0.’ alt=’4+x> 0.’ /> Значит, -4.’ alt=’x> -4.’ />
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом -4′ alt=’x> -4′ />.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
0\ x^-4> 0\ x^+x=x^-4 endright.Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x=-4 endright.Leftrightarrow x=-4′ alt=’log _left ( x^+x right )=log _left ( x^-4 right )Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x^+x=x^-4 endright.Leftrightarrow left <beginx^+x> 0\ x^-4> 0\ x=-4 endright.Leftrightarrow x=-4′ />
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
0 endright.Leftrightarrow left <beginleft (2^<log _left ( 4x+5 right )> right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginsqrt=9\ x> -1frac endright.Leftrightarrow left <begin4x+5=81\ x> -1frac endright.Leftrightarrow left <beginx=19\ x> -1frac endright.’ alt=’2^<log _left ( 4x+5 right )>=9Leftrightarrow left <begin2^frac<<log _left ( 4x+5 right )>>=9\ 4x+5> 0 endright.Leftrightarrow left <beginleft (2^<log _left ( 4x+5 right )> right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginleft ( 4x+5 right )^<frac>=9\ x> -1frac endright.Leftrightarrow left <beginsqrt=9\ x> -1frac endright.Leftrightarrow left <begin4x+5=81\ x> -1frac endright.Leftrightarrow left <beginx=19\ x> -1frac endright.’ />
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
0\ x> 0\ xneq 1 endright.’ alt=’left <begin12-x> 0\ x> 0\ xneq 1 endright.’ />
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие 0′ alt=’x> 0′ />.
8. Решите уравнение .
ОДЗ уравнения: 0′ alt=’x> 0′ />
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Логарифмические уравнения могут встретиться вам и в задании №1 Профильного ЕГЭ по математике, и в задании №12. И если в задании №1 нужно решить простейшее уравнение, то в задаче 12 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать
Логарифм в показателе степени
Для преобразования выражений, содержащих логарифм в показателе степени числа (или выражения), используют основное логарифмическое тождество.
Рассмотрим на примерах, как упростить выражение, содержащее в показателе степени логарифмы.
По свойству степени
от степени с суммой в показателе переходим к произведению степеней
От степени с рациональным показателем переходим к корню; основание степени преобразовываем, чтобы можно было использовать основное логарифмическое тождество:
Применим свойство степени
Значение выражения можно найти двумя способами.
Логарифмы, стоящие в показатели степени, приведем к одинаковым основаниям:
показатель степени, стоящей в основании логарифма, вынесем за знак логарифма, затем внесём в показатель степени числа, стоящего под знаком логарифма:
Сумма логарифмов равна логарифму произведения. Затем применим основное логарифмическое тождество:
Перейдем к произведению степеней, затем каждый множитель преобразуем отдельно:
Выносим показатели степеней из оснований перед логарифмами:
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать
Логарифм: что это? Все формулы. Простейшие уравнения и неравенства
Что такое логарифм
Сейчас речь пойдет о трех страшных буквах: l o g.
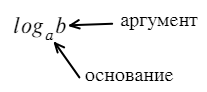
Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?
На самом деле в этом и заключается основная формула (определение логарифма):
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c» . Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182. мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета. Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).
Два нужно четыре раза умножить само на себя, чтобы получить 16.
lg — это логарифм по основанию 10. 10 нужно 3 раза умножить само на себя, чтобы получить 1000.
А теперь посложнее, перейдем по определнию к показательному уравнению :
Следующий пример поможет нам узнать первую формулу логарифмов:
Преобразуем выражение по определению логарифма и получим показательное уравнение. Единица — это же любое значение в нулевой степени?
Тогда можно сделать вывод, что при любом основании и аргументе логарифма, равном 1, все эти логарифмы будут равны нулю.
Нетрудно тогда понять, что есть еще одно следствие:
В какую степень нужно возвести 2, чтобы получить 2? Напряжем все свои извилины и получим — один!
Дальше будут формулы, которые я позволю себе не выводить, чтобы не испугать неискушенных в математике читателей.
Хотя мой вам совет: отследить, откуда эта формула появилась. У логарифмов самое главное помнить, что логарифм — это действие, обратное возведению в степень.
Основное логарифмическое тождество:
В какую степень нужно возвести 3, чтобы получить 9? Значит, логарифм в показателе степени равен двум.
Это единственная формула, где логарифм в показатели степени. Видишь логарифм в степени? Тебе поможет только эта формула.
Еще примерчик, двойка перед логарифмом никак не влияет, формула все так же работает:
А вот квадрат в логарифме тоже быть может, только лучше сначала разложить:
Дальше с этим ничего сделать не сможем.
Дальнейшие формулы тоже уникальны, это тебе не косинус двойного угла.
Видим сложение логарифмов, выпускаем эту формулы:
А вот примерчик, чтобы порадовать тебя этой формулой, только наоборот:
Видим разность логарифмов, выпускаем эту формулы:
А теперь сразу сумма и разность. По отдельности логарифмы не найти, но вместе они и мы сила:
Теперь посмотрим на степени у аргмента логарифма:
А в основании тоже можно? Нужно!
Минус два — это степень у основания:
А все вместе можно? Конечно, логарифмы — это такая свобода:
А здесь нужно будет соединить две формулы: 1) вынесение степени из основания и 2) разность логарифмов
С основными формулами разобрались, теперь для решения более сложных уравнений/выражений.
Формула перехода к новому основанию:
Обрати внимание, чем она отличается от разности логарифмов (4). Тут мы делим один логарифм на другой, а там деление происходит под логарифмом.
Тут все просто, разве что стоит вспомнить, что квадратный корень — это степень одна вторая.
Тут первым действием воспользуемся изучаемой формулой, а дальше каждый логарифм в виде числа, потихонечку−полегонечку.
Последняя формула, меняем местами аргумент и основание логарифма:
Используется тоже нечасто, но если ее не знаешь, то никак не выкрутишься через другие формулы.
Закрепим обе формулы. Используем формулу (9), после (8), а так же не забудь порадовать десятичные дроби — переведи их в обыкновенные, а они порадуют тебя. Теперь посмотрим еще на пару примеров:
Логарифм в логарифме, что может быть прекраснее? Только решенный логарифм в логарифме.
Начинаем с внутреннего:
И постепенно раскрываем каждый последующий:
После того, как с формулами разобрались, (а их всего 9! Согласись, несложно выучить?), перейдем к уравнениям.
Все логарифмические уравнения решаем по одному из двух алгоритмов.
Первый появляется из определения логарифма:
Только не забываем про ОДЗ:
Второй вариант, когда логарифм с одним основанием равен логарифму с точно таким же основнанием:
Не забываем про ОДЗ, тогда получится:
Подставив в ОДЗ x = 15, видим, что все выполняется!
Обязательно только логарифм (без всяких множителей и т.п.) с одним основанием должен быть равен другому логарифму с таким же основанием:
Здесь перед логарифмами стоят разные множители, поэтому прежде всего нужно их внести в логарифм (6 формула), а после убрать логарифмы:
Если стоят одинаковые множители, их можно сократить сразу или сократить на общий множитель:
Бывает, что с одной стороны уравнения есть сумма логарифмов (4) или обычное число, сокращать их сразу нельзя! Только после того, как приведем и левую, и правую часть к одному логарифму:
Что же касается неравенств, убирать логарифмы можно так же, как и в уравнениях, только здесь нужно внимательно смотреть на значение оснований. Если основание логарифма лежит в диапазоне 0 1, то убираем логарифмы без смены знака и дорешиваем обычное неравенство:
- Л О Г — это не три страшные буквы, а обратное действие возведению в степень.
- Хоть формул и целых девять, но они никак не пересекаются. Решая пример и ориентируясь в формулах, ты будешь однозначно выбирать необходимую формулу.
- Видишь логарифм — ищи ОДЗ и решай его в первую очередь!
- Решение уравнений происходит по одному из двух вариантов и больше никак.
- В неравенствах главное — помнить об основании логарифма, когда зачеркиваем логарифмы.
💡 Видео
Алгебра 11 класс. Логарифм в показателе степени.Скачать
Решение логарифмических уравнений. Вебинар | МатематикаСкачать
ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать
✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать
ЛОГАРИФМ В СТЕПЕНИ? ЭТО КАК? 😉 #shorts #математика #егэ #огэ #профильныйегэСкачать
ЛОГАРИФМЫ с нуля за 25 минут | ЕГЭ Математика | Аня Матеманя | ТопскулСкачать
Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать
Умножаем логарифмы В УМЕ🧠Скачать
КАК СЧИТАТЬ ЛОГАРИФМЫ? #егэматематика2022 #егэ2022 #логарифмы #математика #егэ #огэ #shortsСкачать
Логарифмическое уравнение / Как решить?Скачать
Логарифмы в ЕГЭ⚡️что получилось?!Скачать
Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать
Логарифмические уравнения. 11 класс.Скачать
Логарифмы с нуля за 30 минут. Логарифмы 10 класс ЕГЭ профиль математика | УмскулСкачать
ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ С ЛОГАРИФМОМ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать
ПОКАЗАТЕЛЬНОЕ УРАВНЕНИЕ С ЛОГАРИФМОМ ЧАСТЬ I. Готовимся к ЕГЭ вместе #shorts #математика #егэ #огэСкачать
10 класс. Алгебра. Логарифмические уравнения, сводящиеся к квадратным.Скачать
