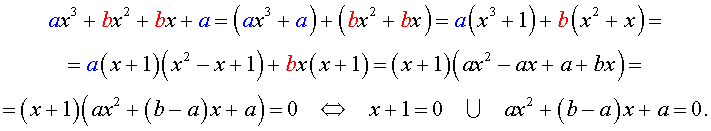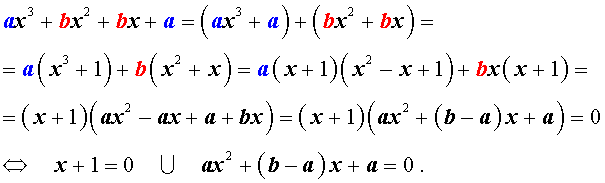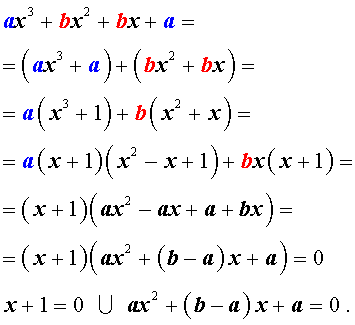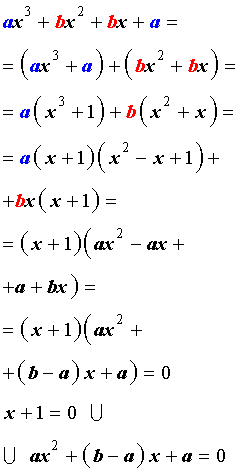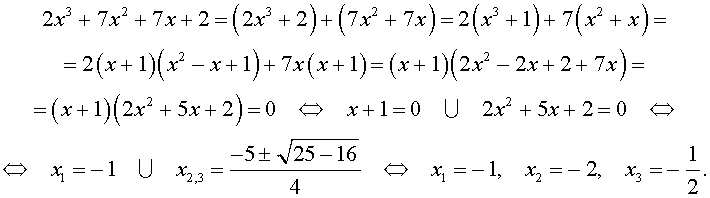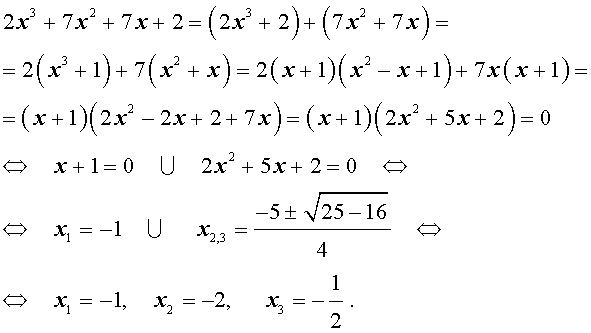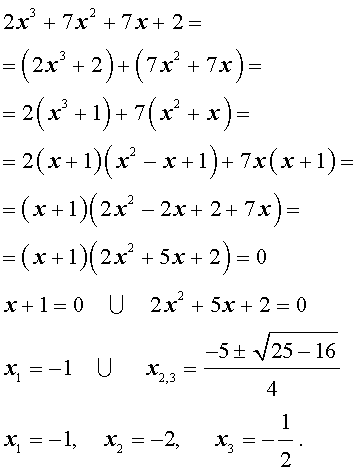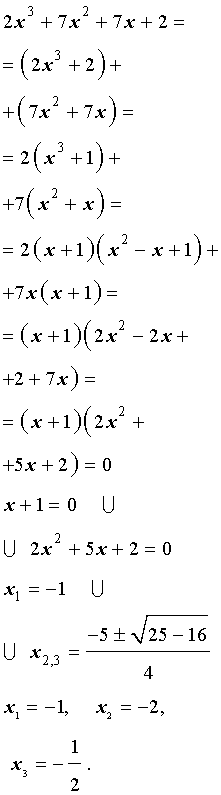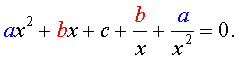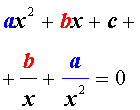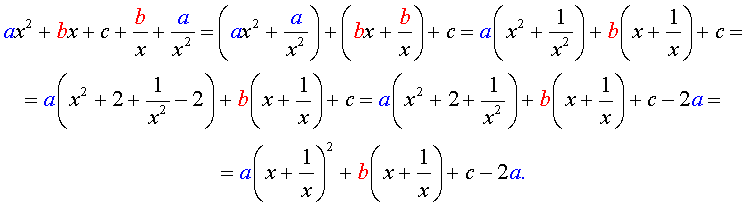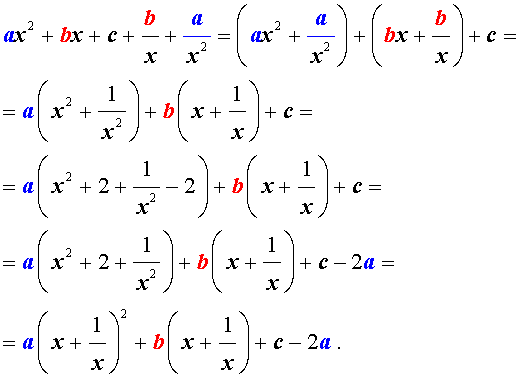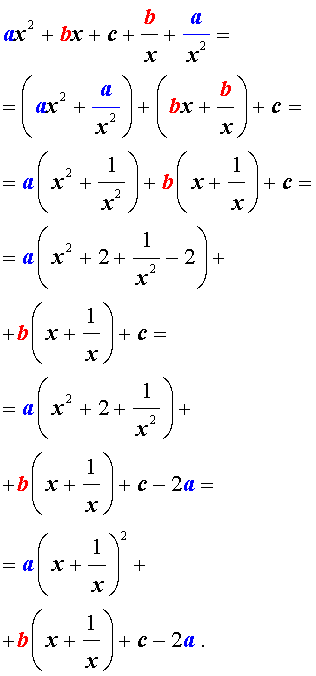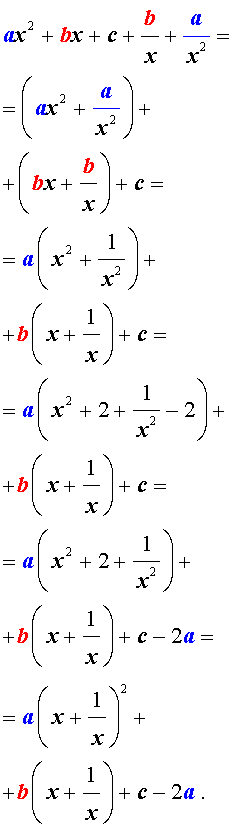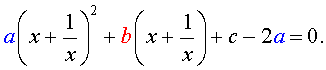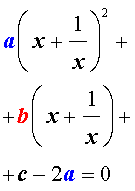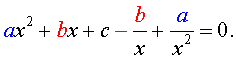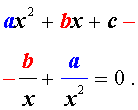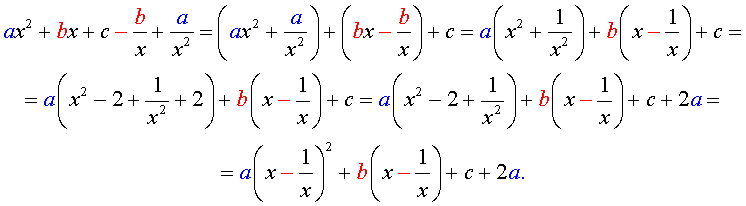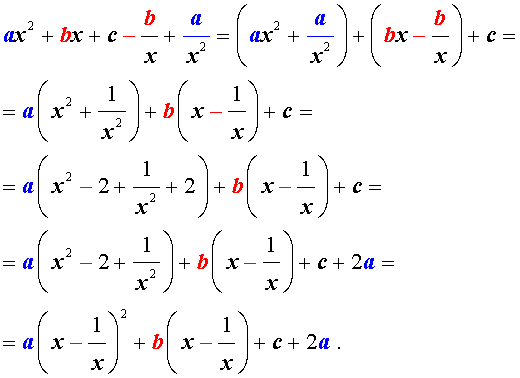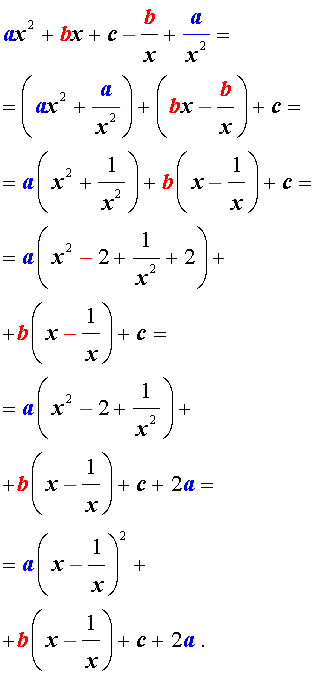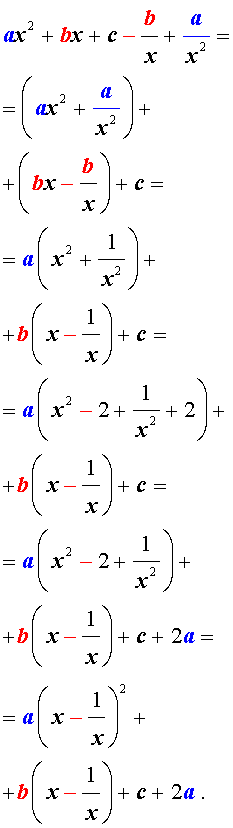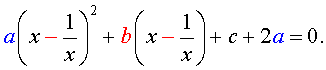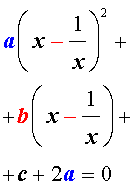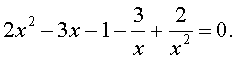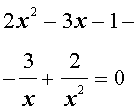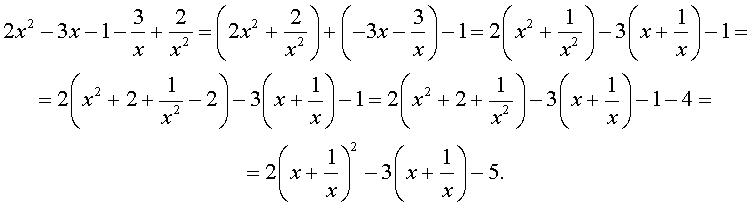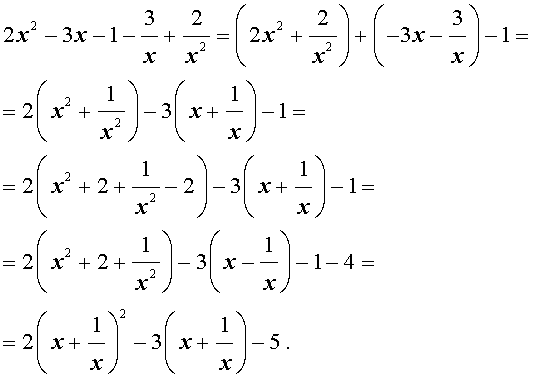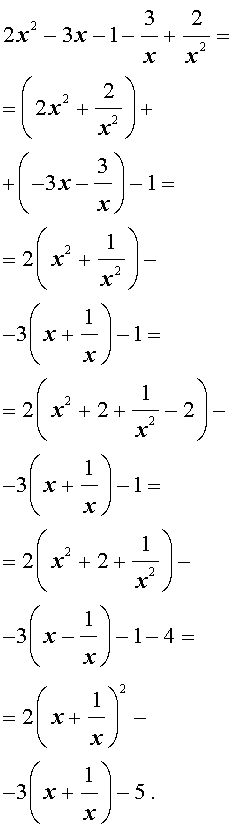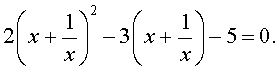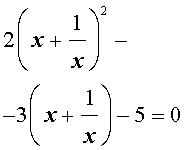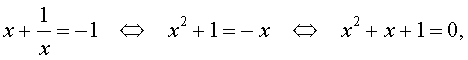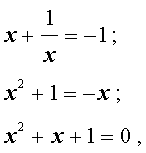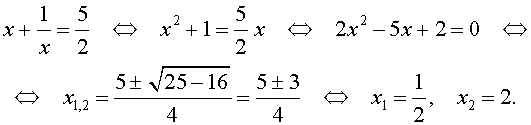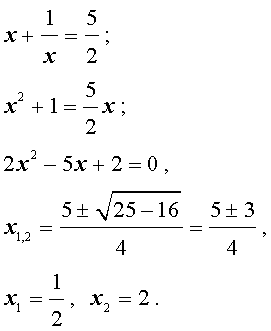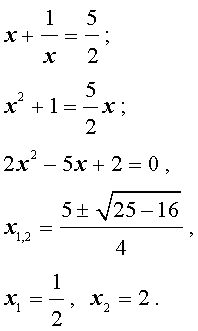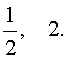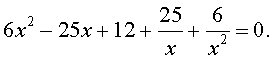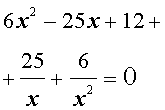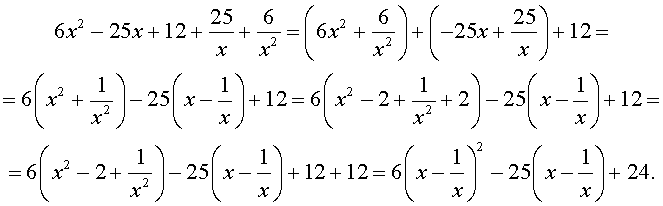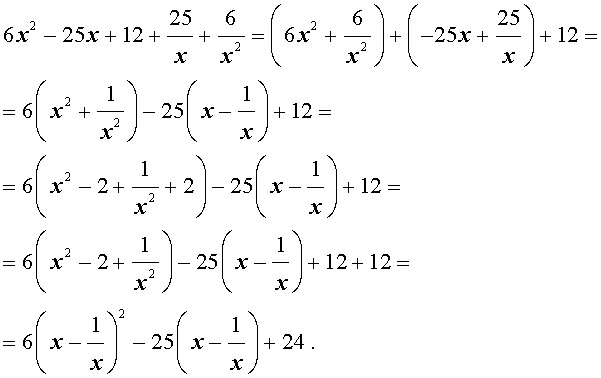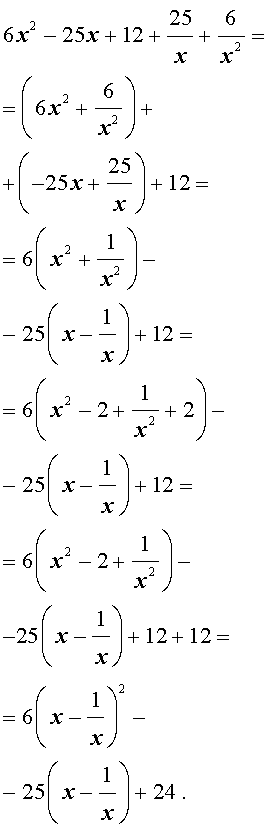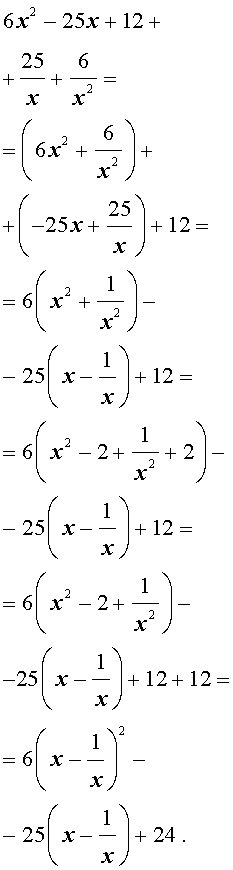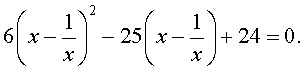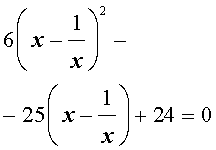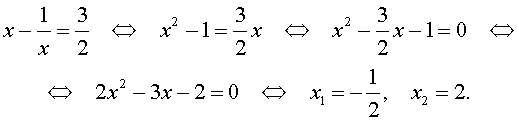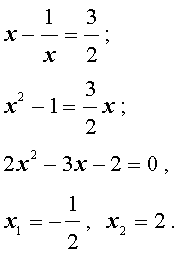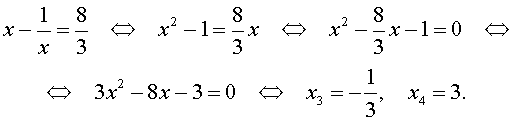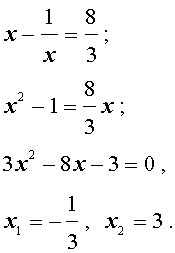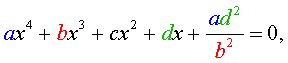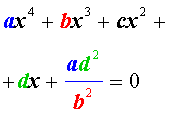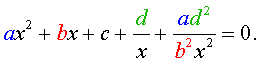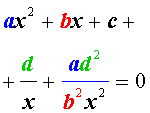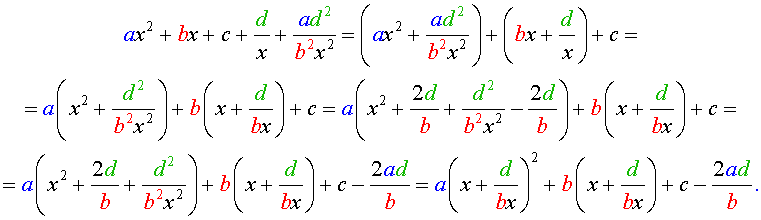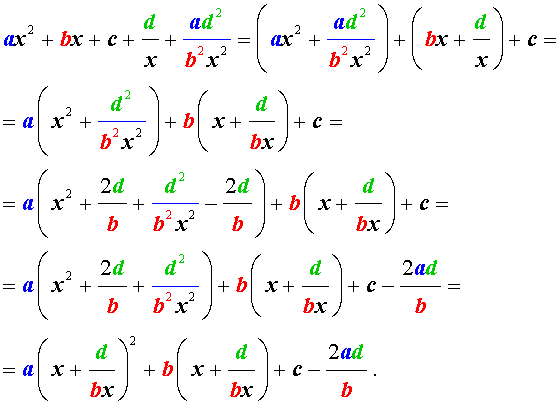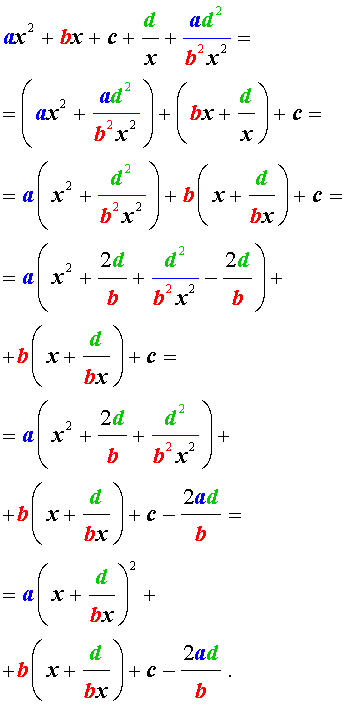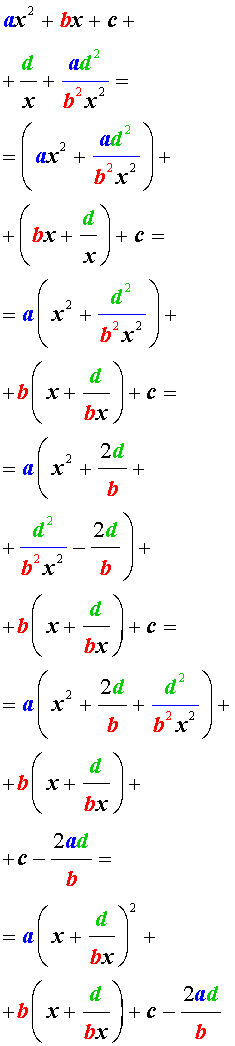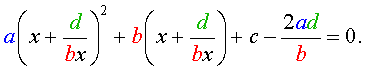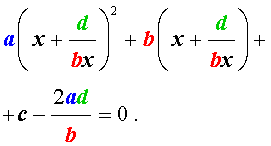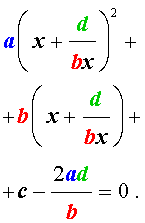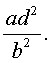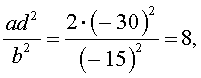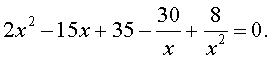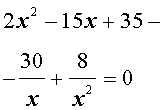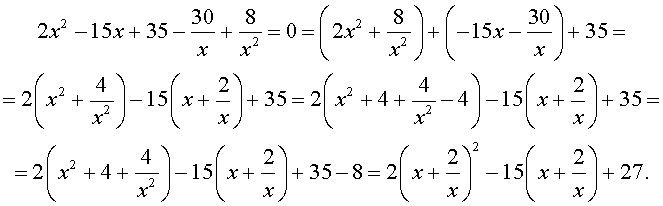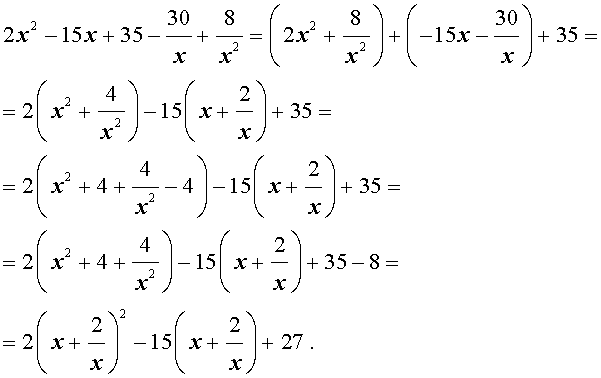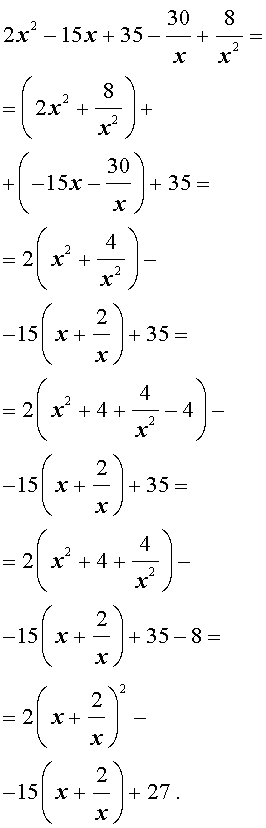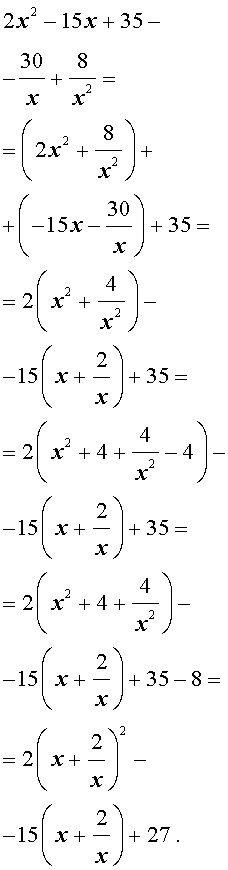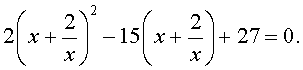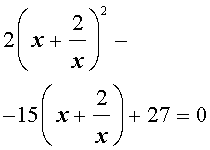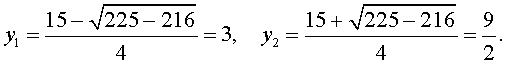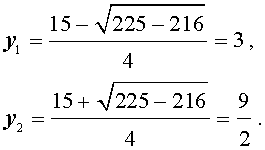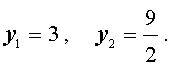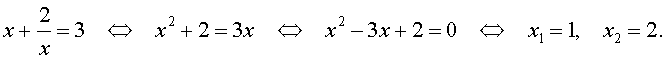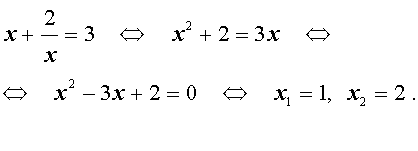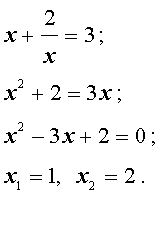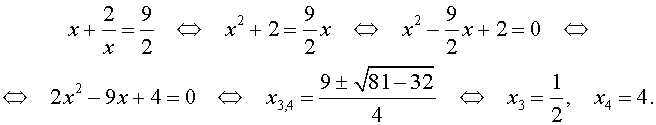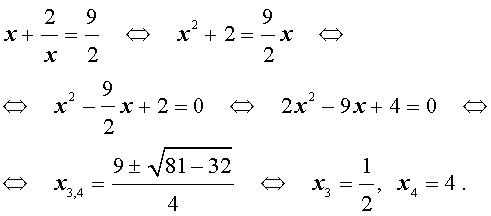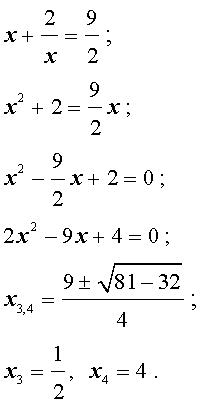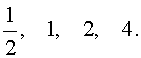возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
- Возвратные (симметричные) уравнения 3-ей степени
- Возвратные (симметричные) уравнения 4-ой степени
- Обобщенные возвратные уравнения 4-ой степени
- Решение уравнений четвертой степени
- Решение двучленного уравнения четвертой степени
- Решение возвратного уравнения четвертой степени
- Решение биквадратного уравнения
- Решение уравнений четвертой степени с рациональными корнями
- Решение уравнений четвертой степени по методу Феррари
- Уравнение четвертой степени
- 💥 Видео
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| a x 3 + b x 2 + b x + a = 0, | (1) |
где a , b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
Пример 1 . Решить уравнение
| 2x 3 + 7x 2 + 7x + 2 = 0. | (2) |
Решение . Разложим левую часть уравнения (2) на множители:
Ответ :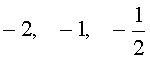
Видео:Уравнение четвертой степениСкачать

Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| a x 4 + b x 3 + cx 2 + + b x + a = 0, | (3) |
а также уравнения вида
| a x 4 + b x 3 + cx 2 – – b x + a = 0, | (4) |
Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
Если теперь обозначить
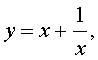 | (7) |
то уравнение (6) станет квадратным уравнением:
| a y 2 + b y + c – 2 a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
Если теперь обозначить
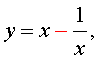 | (11) |
то уравнение (10) станет квадратным уравнением:
| a y 2 + b y + c + 2 a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (4) завершено.
Пример 2 . Решить уравнение
| 2x 4 – 3x 3 – x 2 – – 3x + 2 = 0. | (13) |
Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
Если теперь обозначить
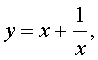 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y 2 – 3y – 5 = 0. | (17) |
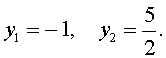 | (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ :
Пример 3 . Решить уравнение
| 6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0. | (19) |
Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
Если теперь обозначить
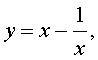 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y 2 – 25y + 24 = 0. | (23) |
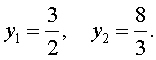 | (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ :
Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
где a , b , c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
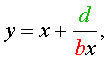 | (28) |
то уравнение (27) станет квадратным уравнением:
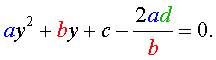 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (25) завершено.
Пример 4 . Решить уравнение
| 2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0. | (30) |
Решение . Введем для коэффициентов уравнения (30) следующие обозначения
и найдем значение выражения
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
Если теперь обозначить
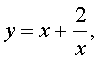 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y 2 – 15y + 27 = 0. | (34) |
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ :
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение уравнений четвертой степени
Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.
Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.
Видео:9 класс. Алгебра. Решение уравнений четвертой степени. Возвратные уравнения.Скачать

Решение двучленного уравнения четвертой степени
Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .
Для решения этого типа уравнений применяются формулы сокращенного умножения:
A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0
Остается лишь найти корни квадратных трехчленов.
Решить уравнение четвертой степени 4 x 4 + 1 = 0 .
Решение
Для начала проведем разложение многочлена 4 x 4 + 1 на множители:
4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )
Теперь найдем корни квадратных трехчленов.
2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i
2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i
Мы получили четыре комплексных корня.
Ответ: x = 1 2 ± i и x = — 1 2 ± i .
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение возвратного уравнения четвертой степени
Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0
х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:
A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0
Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :
A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0
Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.
Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .
Решение
Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :
2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0
2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0
Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2
2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0
Решим полученное квадратное уравнение:
D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3
Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .
Решим первое уравнение:
x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4
Решим второе уравнение:
x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2
Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .
Видео:Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать

Решение биквадратного уравнения
Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.
Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .
Решение
Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:
2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3
Следовательно, x 2 = 1 2 или x 2 = — 3 .
Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .
Ответ: x = ± 1 2 и x = ± i · 3 .
Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .
Решение
Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:
16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9
Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .
Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .
Видео:Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

Решение уравнений четвертой степени с рациональными корнями
Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».
Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Решение уравнений четвертой степени по методу Феррари
Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.
Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.
Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .
Решение
Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.
Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0
Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .
Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0
x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0
x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0
Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .
Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .
Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Уравнение четвертой степени
Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех значений неизвестного (неизвестных), при которых соблюдается верное равенство. Такие значения неизвестного (неизвестных) являются корнями или решением уравнения.
Уравнение вида ах 4 + bх 3 + сх 2 + dх + е = 0 называется уравнением 4-й степени с одним неизвестным. В результате решения уравнения получается 4 комплексных или вещественных корня.
Для решения приведенного уравнения 4-й степени вида: х 4 + Ах 3 + Вх 2 +Сх + D = 0 можно воспользоваться методом Феррари.
Составим кубическое уравнение: у 3 — Ву 2 + (АС — 4D)у — А 2 D + 4ВD — С 2 = 0.
Решаем полученное уравнение, находим один из его вещественных корней у0, который используем для дальнейшего нахождения корней квадратных уравнений.
Получаем и решаем два квадратных уравнения: 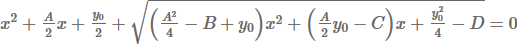
Если дано биквадратное уравнение 4-й степени вида: Ах 4 + Вх 2 + С = 0 и нужно найти его корни, можно свести его к квадратному, заменив переменную х 2 на у (у = х 2 ). В результате получим уравнение вида: Ау 2 + Ву + С = 0. Далее решаем квадратное уравнение через дискриминант.
Если дано возвратное уравнение 4-й степени вида: Ах 4 + Вх 3 + Сх 2 + Вх + А = 0 и нужно найти его корни, следует разделить уравнение на х 2 , получим:
Ах 2 + Вх + С + В / х + А / х 2 = 0.
Группируем и выносим коэффициенты за скобки: Ах 2 + А / х 2 + Вх + В / х + С = 0; А(х 2 + 1 / х 2 ) + В(х + 1 / х) + С = 0.
Произведем замену переменных: х + 1 / х = у; х 2 + 1 / х 2 = у 2 — 2, получим: А(у 2 — 2) + Ву + С = 0.
Сводим уравнение 4-й степени к квадратному уравнению и решаем его через дискриминант Ау 2 + Ву + С — 2А = 0.
Находим у1 и у2, после чего возвращаемся к замене и находим корни.
Быстро решить любое уравнение вы сможете с помощью представленного на сайте онлайн калькулятора.
💥 Видео
8 класс. Алгебра. Решение уравнений четвертой степени.Скачать

8 класс. Алгебра. Решение уравнений четвертой степени.Скачать

Как решать возвратные уравнения?Скачать

Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

УДИВИТЕЛЬНЫЙ способ решения уравнения 4-ой степениСкачать

Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать

10 класс. Алгебра. Уравнение четвертой степени.Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать