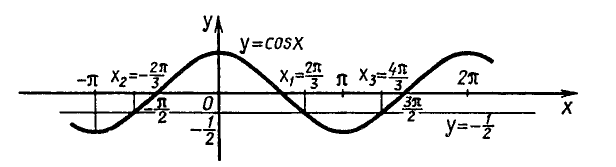
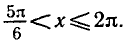
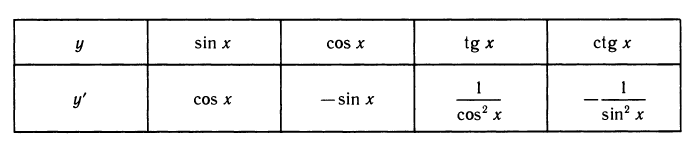
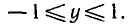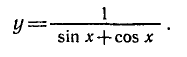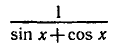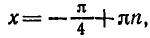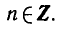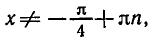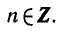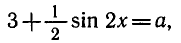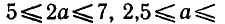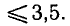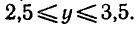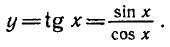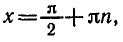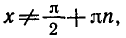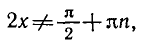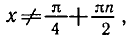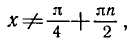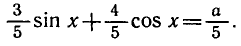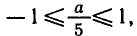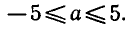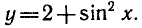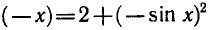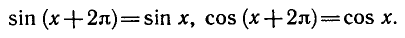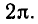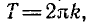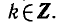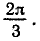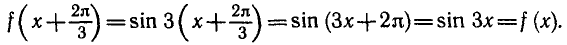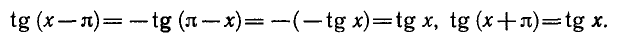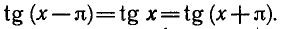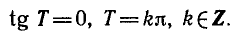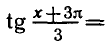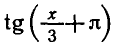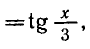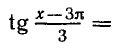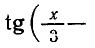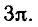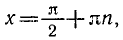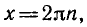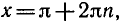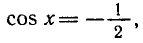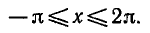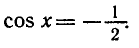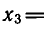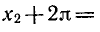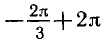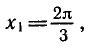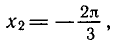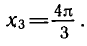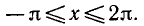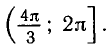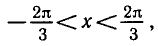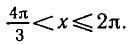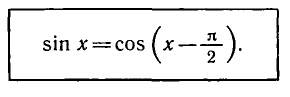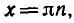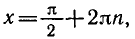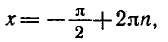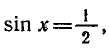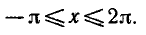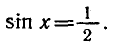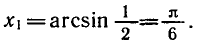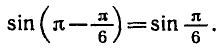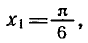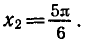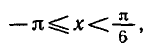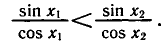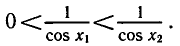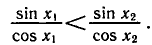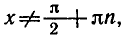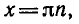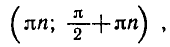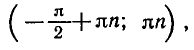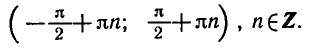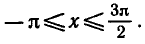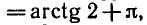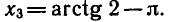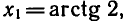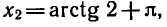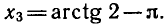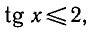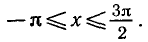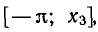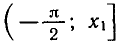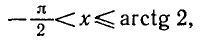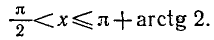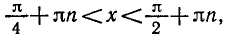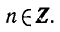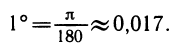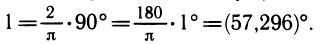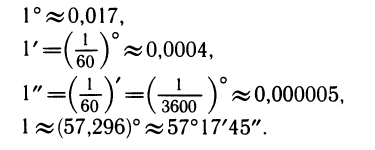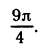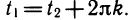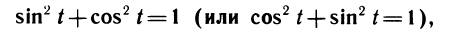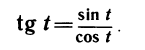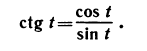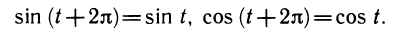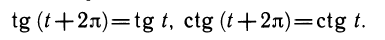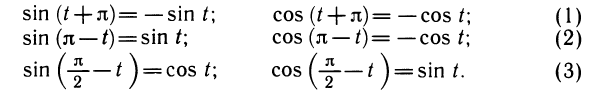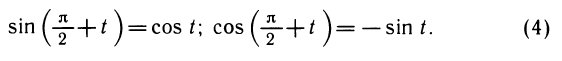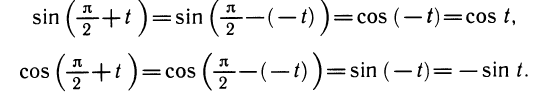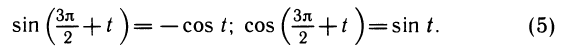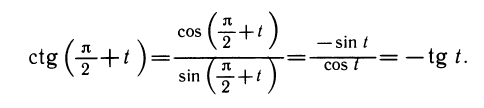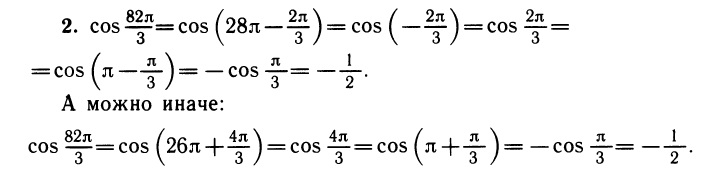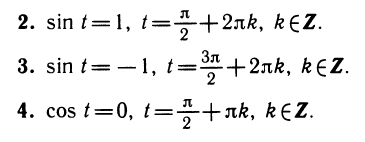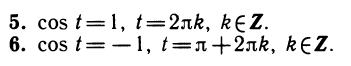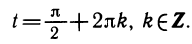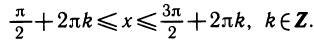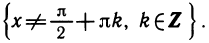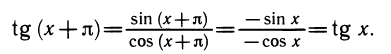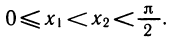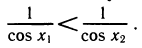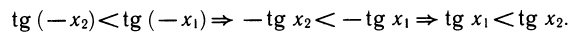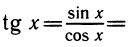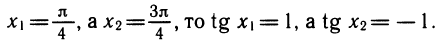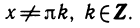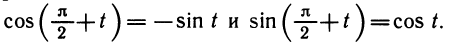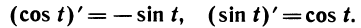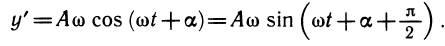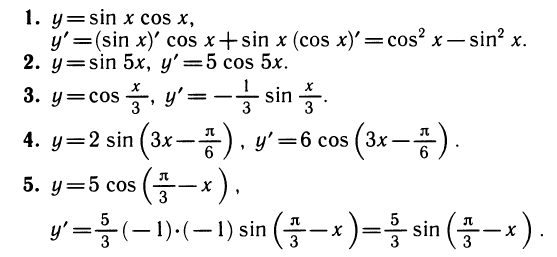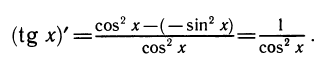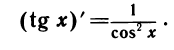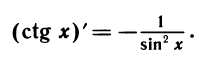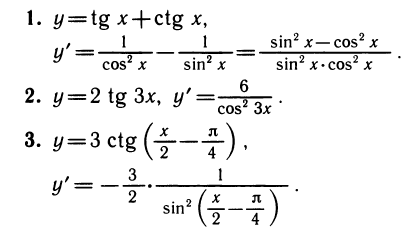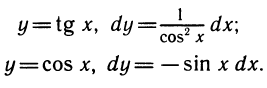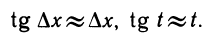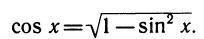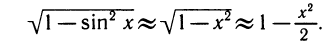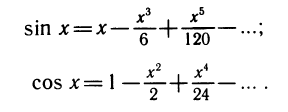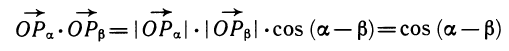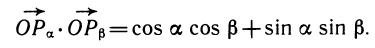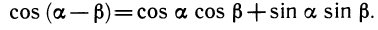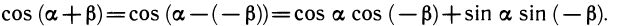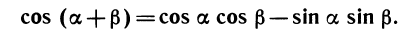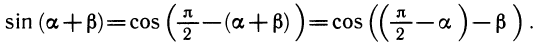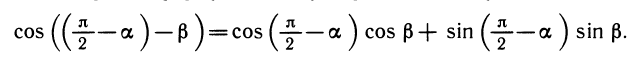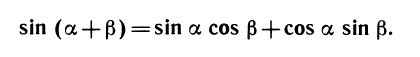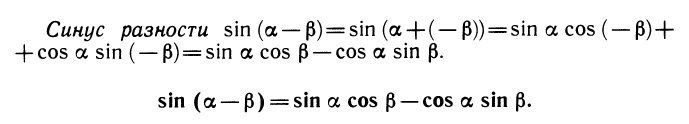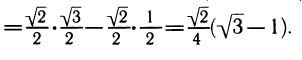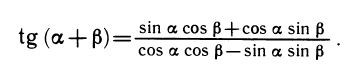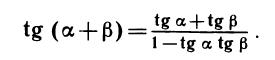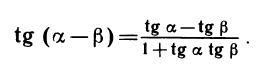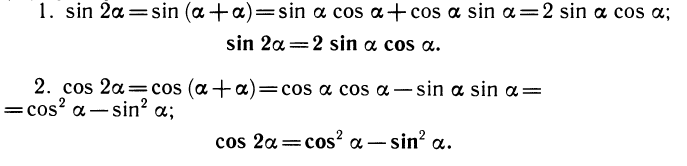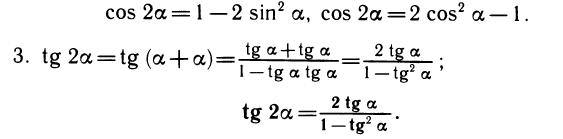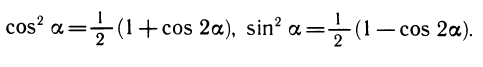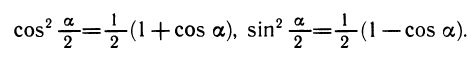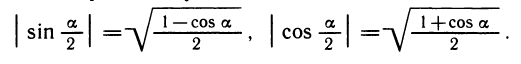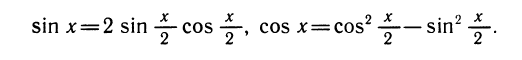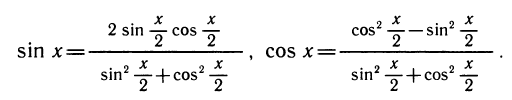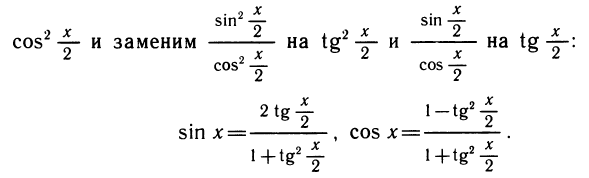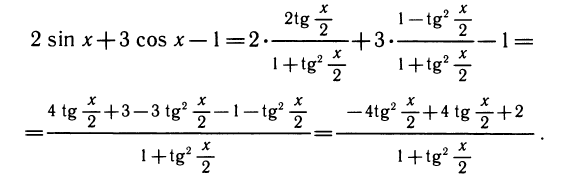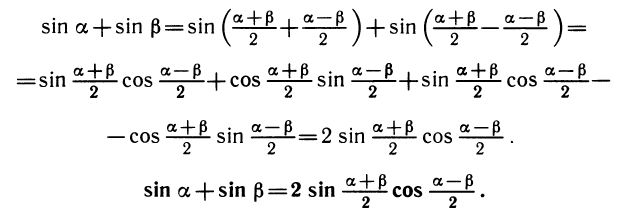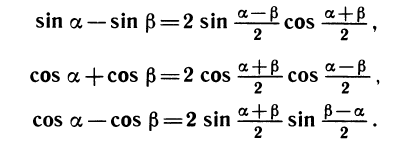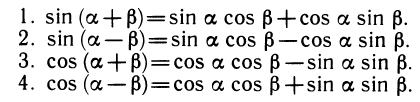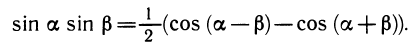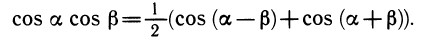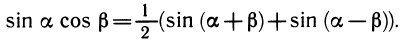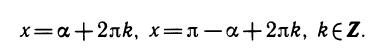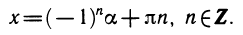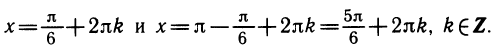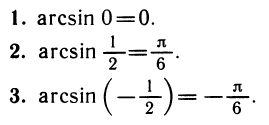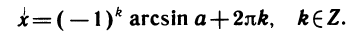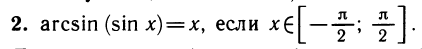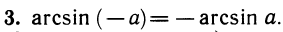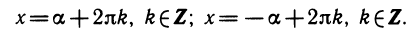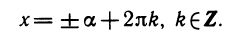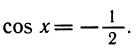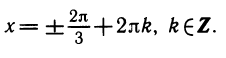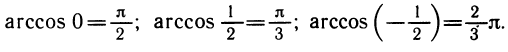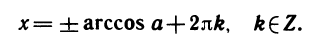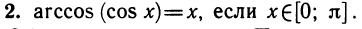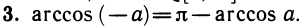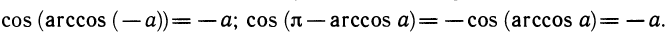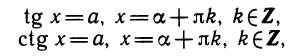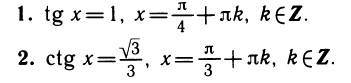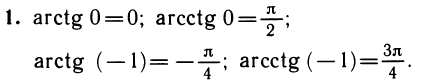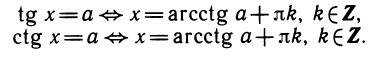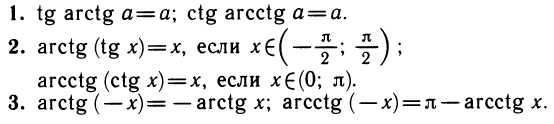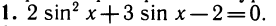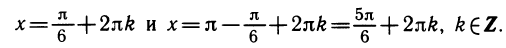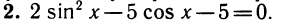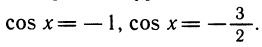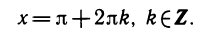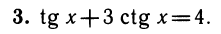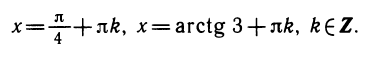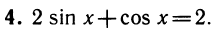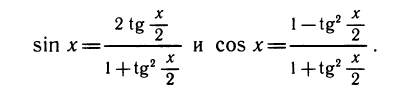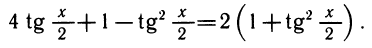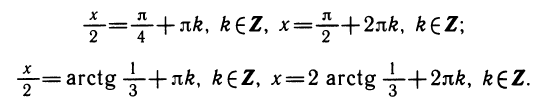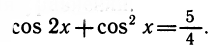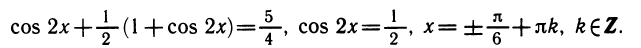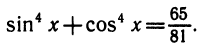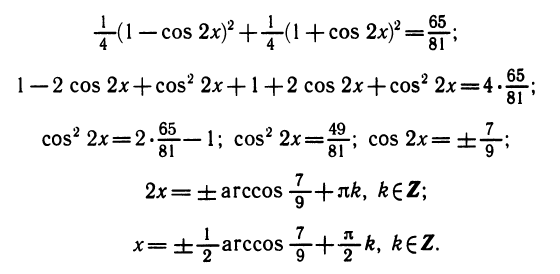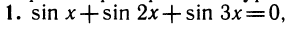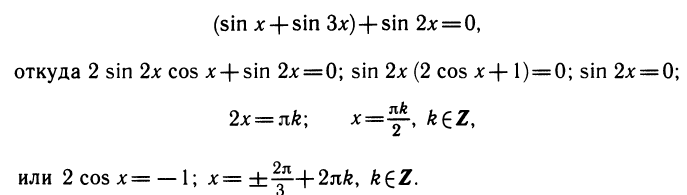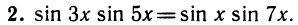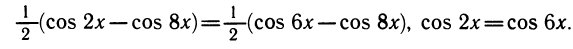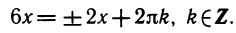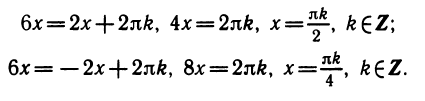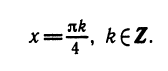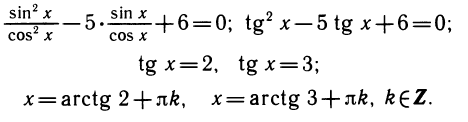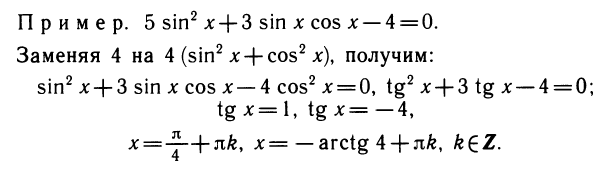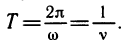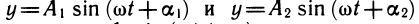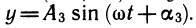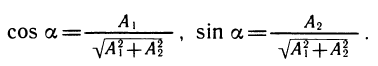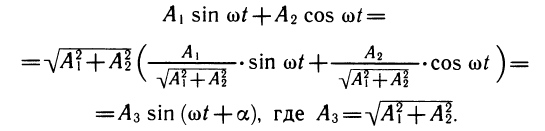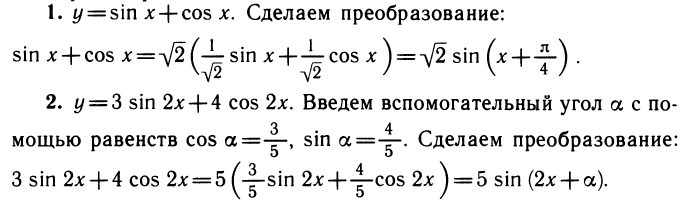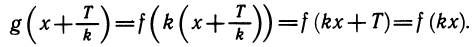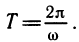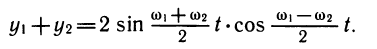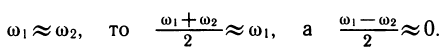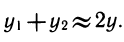Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
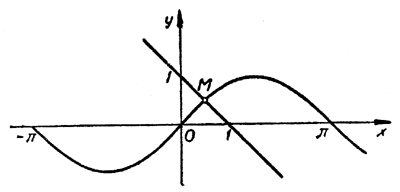
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
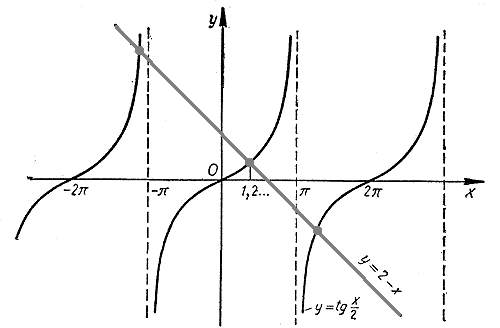
Графики функций у = tg x /2 и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
- Геометрия. Урок 1. Тригонометрия
- Тригонометрия в прямоугольном треугольнике
- Тригонометрия: Тригонометрический круг
- Основное тригонометрическое тождество
- Тригонометрия: Таблица значений тригонометрических функций
- Тригонометрия: градусы и радианы
- Тригонометрия: Формулы приведения
- Тригонометрия: Теорема синусов
- Тригонометрия: Расширенная теорема синусов
- Тригонометрия: Теорема косинусов
- Примеры решений заданий из ОГЭ
- Тригонометрия: Тригонометрические уравнения
- Тригонометрические функции с примерами решения и образцами выполнения
- Область определения и множество значений тригонометрических функций
- Четность, нечетность, периодичность тригонометрических функций
- Функция у = cos x, ее свойства и график
- Функция y=sin x, ее свойства и график
- Функция y=tg x, ее свойства и график
- Углы и их измерение
- Вращательное движение и его свойства
- Определение тригонометрических функций
- Периодичность
- Знаки тригонометрических функций
- Четность
- Формулы приведения
- Значения тригонометрических функций
- Решение простейших тригонометрических уравнений
- Исследование тригонометрических функций
- Основные свойства синуса и косинуса
- Графики синуса и косинуса
- Исследование тангенса и котангенса
- Производные тригонометрических функций
- Приближенные формулы
- Тождественные преобразования
- Формулы сложения
- Формулы удвоения
- Тригонометрические функции половинного угла
- Преобразование суммы тригонометрических функций в произведение и обратные преобразования
- Тригонометрические уравнения
- Арксинус
- Арккосинус
- Арктангенс
- Решение тригонометрических уравнений
- Гармонические колебания
- Периодические функции
- Разложение на гармоники
- Тригонометрические и обратные тригонометрические функции
Видео:Отбор корней тригонометрического уравнения с помощью графикаСкачать

Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Видео:ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 11 класс графики тригонометрических функцийСкачать

Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Видео:Отбор корней по окружностиСкачать

Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрия: Таблица значений тригонометрических функций
Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Видео:10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать

Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Видео:Алгебра 10 класс. 16 октября. Строим тригонометрические графики синусаСкачать

Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Видео:ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙСкачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Видео:Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.Скачать

Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Видео:Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать

Тригонометрические функции с примерами решения и образцами выполнения
Тригонометрические функции — служат прежде всего для описания разнообразных периодических процессов. С периодически повторяющимися ситуациями человек сталкивается повсюду. Его жизнь сопровождают различные астрономические явления — восход и заход Солнца, изменение фаз Луны, чередование времен года, положение звезд на небе, затмения и движения планет. Человек давно заметил, что все эти явления возобновляются периодически. Жизнь на Земле тесно связана с ними, и поэтому неудивительно, что астрономические наблюдения явились источником многих математических открытий.
Биение сердца, цикл в жизнедеятельности организма, вращение колеса, морские приливы и отливы, заполненность городского транспорта, эпидемии гриппа — в этих многообразных примерах можно найти общее: эти процессы периодичны.
Открывая утром газету, мы часто читаем сообщение об очередном запуске искусственного спутника Земли. Обычно в сообщении указываются наименьшее и наибольшее расстояния спутника от поверхности Земли и период его обращения. Если сказано, что период обращения спутника составляет 92 мин, то мы понимаем, что его положение относительно Земли в какой-то момент времени и через каждые 92 мин с этого момента будет одинаковым. Так мы приходим к понятию периодической функции как функции, обладающей периодом, т. е. таким числом Т, что значения функции при значениях аргумента, отличающихся на Т, 2Т, ЗТ и т. д., будут одинаковыми.
Астрономия, которая дает нам наиболее наглядное представление о периодических процессах, определяет положение объектов в небесной сфере с помощью углов. Можно сказать так: в качестве аргумента периодических функций очень часто выступает угол. Поэтому в нашей беседе мы обсудим вопрос об измерении углов.
Видео:Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Область определения и множество значений тригонометрических функций
Вы знаете, что каждому действительному числу х соответствует единственная точка единичной окружности, получаемая
поворотом точки (1; 0) на угол х радиан. Для этого угла
определены sin х и cos х. Тем самым каждому действительному числу х поставлены в соответствие числа sin х и cos х, т. е. на множестве R всех действительных чисел определены функции
y = sin x и у = cos x.
Таким образом, областью определения функций y = sin x и
у = cos x является множество R всех действительных чисел.
Чтобы найти множество значений функции y = sin х, нужно
выяснить, какие значения может принимать у при различных значениях х, т. е. установить, для каких значений у есть такие значения х, при которых sin x = y. Известно, что уравнение
sin x = a имеет корни, если 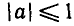
|а |> 1 .
Томсон Уильям, лорд Кельвин (1824— 1907) — английский физик, президент Лондонского королевского общества. Дал одну из формулировок второго начала термодинамики, предложил абсолютную шкалу температур (шкалу Кельвина).
Следовательно, множеством значений функции у = sin x
является отрезок
Аналогично множеством значений функции у = сos x также
является отрезок
Задача:
Найти область определения функции
Найдем значения х, при которых выражение —
не имеет смысла, т. е. значения х, при которых знаменатель равен
нулю. Решая уравнение sin x + cos х = 0, находим tg x = — 1,
Следовательно, областью определения данной функции являются все значения
Задача:
Найти множество значений функции y = 3 + sin х cos х.
Нужно выяснить, какие значения может принимать у при
различных значениях х, т. е. установить, для каких значений а
уравнение 3 + sin х cos х = а имеет корни. Применяя формулу
синуса двойного угла, запишем уравнение так:
откуда sin2x = 2a — 6. Это уравнение имеет корни, если
|2а — 6| = 1, т. е. если 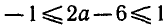
Следовательно, множеством значений данной функции является промежуток
Функция y = tg x определяется формулой
Эта функция определена при тех значениях х, для которых 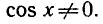
Известно, что cos x = 0 при
Следовательно, областью определения функции y = tg х является множество чисел
Так как уравнение tg x = a имеет корни при любом
действительном значении а, то множеством значений функции
y = tg х является множество R всех действительных чисел.
Функции y = sin x, у = cos x, y = tg x называются
тригонометрическими функциями.
Задача:
Найти область определения функции y = sin Зх + tg 2х.
Нужно выяснить, при каких значениях х выражение
sin 3x + tg 2х имеет смысл. Выражение sin Зх имеет смысл при
любом значении х, а выражение tg 2х — при 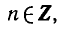
Следовательно, областью определения данной функции является множество действительных чисел
Задача:
Найти множество значений функции
у = 3 sin x + 4 cos х.
Выясним, при каких значениях а уравнение 3 sin x + 4 cos x = a имеет корни. Поделим уравнение на
Так как 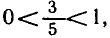
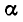
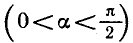
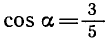
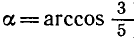
Тогда 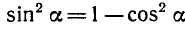
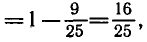
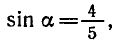
так как 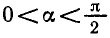
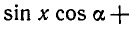
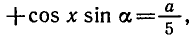
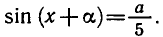
Ответ.
Четность, нечетность, периодичность тригонометрических функций
Вы знаете, что для любого значения х верны равенства
sin ( — x ) = — sin x, cos ( — x) = — cos x.
Следовательно, y = sin х — нечетная функция, а у = cos х —
четная функция. Так как для любого значения х из области
определения функции y — tg x верно равенство tg (— х)= — tg х,
то y = tg х — нечетная функция.
Задача:
Выяснить, является ли функция
четной или нечетной.
Используя формулу приведения, запишем данную функцию
так:
Имеем 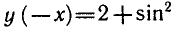
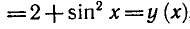
Известно, что для любого значения х верны равенства
Из этих равенств следует, что значения синуса и косинуса
периодически повторяются при изменении аргумента на
Такие функции называются периодическими с периодом
Функция f (x) называется периодической, если существует такое число 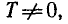
Число 7 называется периодом функции f (х).
Из этого определения следует, что если х принадлежит области определения функции f (х), то числа х + T , х — Т и вообще
числа х + Tn , 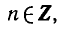
этой периодической функции и f (х + Tn ) = f (х),
Покажем, что число 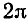
Пусть T > 0 — период косинуса, т. е. для любого х выполняется равенство cos (х + T) = cos х. Положив х = 0, получим
cos T = 1 . Отсюда
Так как T > 0 , то T может принимать значения 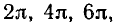
Можно доказать, что наименьший положительный период функции у = sin х также равен
Задача:
Доказать, что f (x) = sin 3 x — периодическая
функция с периодом
Если функция f (х) определена на всей числовой оси, то для
того, чтобы убедиться в том, что она является периодической
с периодом T, достаточно показать, что для любого х верно
равенство f (х + T ) = f (х). Данная функция определена для всех 
Покажем, что функция tg х является периодической с периодом
Если х принадлежит области определения этой функции, т. е. 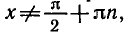
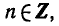
Следовательно, 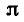
Покажем, что 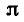
Пусть T — период тангенса, тогда tg ( x + T ) = tg x , откуда
при х = 0 получаем:
Так как наименьшее целое положительное k равно 1, то 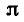
наименьший положительный период функции tg х.
Задача:
Доказать, что 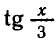
с периодом
Так как 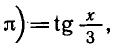
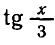
Периодическими функциями описываются многие физические
процессы (колебания маятника, вращение планет, переменный
ток и т. д.).
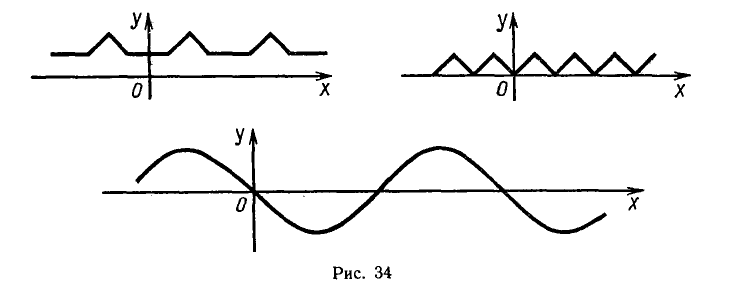
На рисунке 34 изображены графики некоторых периодических функций.
Отметим, что на всех последовательных отрезках числовой
прямой, длина которых равна периоду, график периодической
функции имеет один и тот же вид.
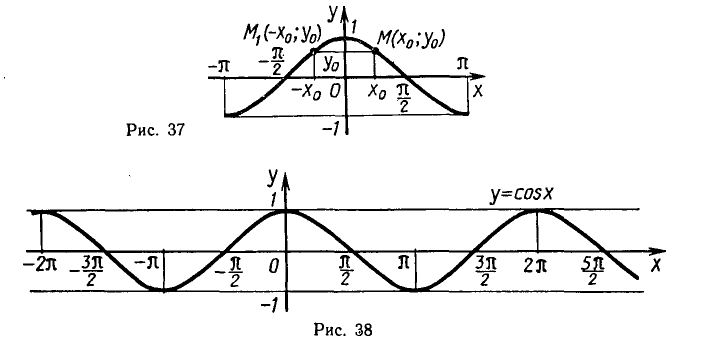
Функция у = cos x, ее свойства и график
Напомним, что функция у = cos х определена на всей числовой прямой и множеством ее значений является отрезок [— 1; 1].
Следовательно, график этой функции расположен в полосе между прямыми у = — 1 и у = 1.
Так как функция у = cos х периодическая с периодом 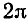
достаточно построить ее график на каком-нибудь промежутке длиной 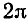
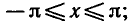
промежутках, получаемых сдвигами выбранного отрезка на 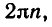
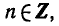
Функция у = cos х является четной. Поэтому ее график симметричен относительно оси Оу. Для построения графика на отрезке 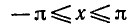
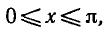
Прежде чем перейти к построению графика, покажем, что
функция у = cos х убывает на отрезке
В самом деле, при повороте точки Р (1; 0) вокруг начала координат против часовой стрелки на угол от 0 до 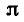
т. е. cos х, уменьшается от 1 до — 1. Поэтому если 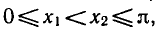

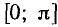
Используя свойство убывания функции y = cos x на отрезке 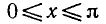
построим его на этом отрезке (рис. 36).
Пользуясь свойством четности функции у = cos х, отразим
построенный на отрезке 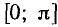
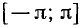
Так как у = cos х — периодическая функция с периодом 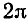
и ее график построен на отрезке 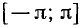
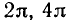
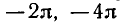
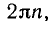
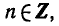
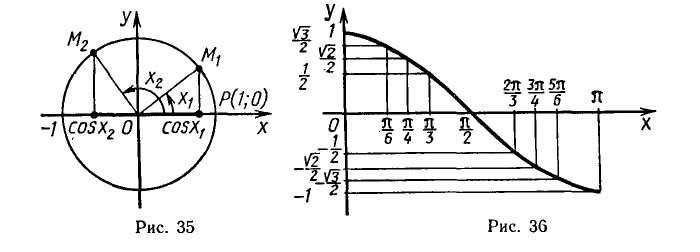
Итак, график функции у = cos x: построен геометрически на
всей числовой прямой, начиная с построения его части на отрезке 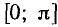
опираясь на свойства этой функции на отрезке 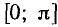
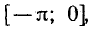
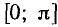
Перечислим основные свойства функции у = cos х;
1) Область определения — множество R всех действительных
чисел.
2) Множество значений — отрезок [— 1; 1].
3) Функция у = cos х периодическая с периодом 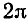
4) Функция у = cos х четная.
5) Функция у = cos х принимает:
— значение, равное 0, при 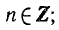
— наибольшее значение, равное 1, при 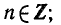
— наименьшее значение, равное — 1, при 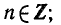
— положительные значения на интервале 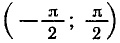
интервалах, получаемых сдвигами этого интервала на 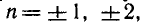
— отрицательные значения на интервале 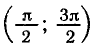
интервалах, получаемых сдвигами этого интервала на 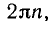
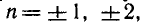
6) Функция у = cos х:
— возрастает на отрезке 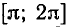
сдвигами этого отрезка на 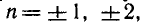
— убывает на отрезке 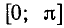
сдвигами этого отрезка на 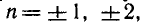
Задача:
Найти все корни уравнения
принадлежащие отрезку
Построим графики функций у = сos х и 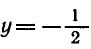
отрезке (рис. 39). Эти графики пересекаются в трех точках,
абсциссы которых 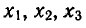
На отрезке 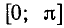
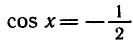
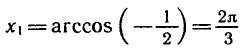
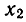
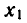
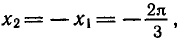
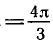
Ответ.
Задача:
Найти все решения неравенства 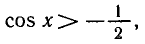
Из рисунка 39 видно, что график функции у = cos x лежит
выше графика функции 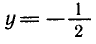
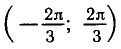
Ответ.
Функция y=sin x, ее свойства и график
Функция y = sin x определена на всей числовой прямой, является нечетной и периодической с периодом 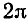
построить таким же способом, как и график функции у = cos x,
начиная с построения, например, на отрезке 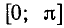
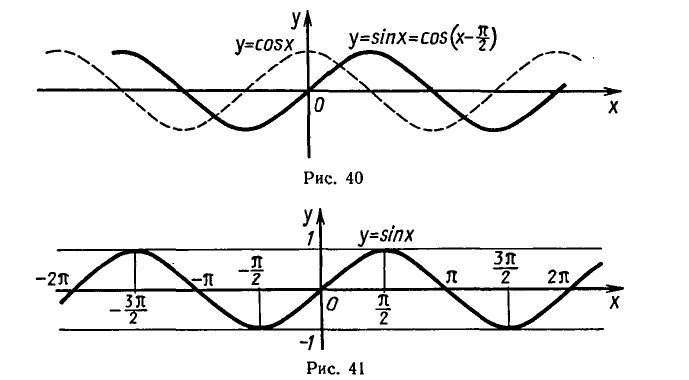
Эта формула показывает, что график функции у = sin х можно
получить сдвигом графика функции у = соs х вдоль оси абсцисс
вправо на 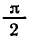
График функции у = sin х изображен на рисунке 41.
Кривая, являющаяся графиком функции у = sin х, называется
синусоидой.
Так как график функции у = sin х получается сдвигом графика функции у = соs х, то свойства функции у = sin х можно получить из свойств функции у = соs x.
Перечислим основные свойства функции у = sin х :
1) Область определения — множество Я всех действительных чисел.
2) Множество значений — отрезок [— 1; 1].
3) Функция у = sin x периодическая с периодом 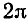
4) Функция у = sin х нечетная.
5) Функция y = sin x принимает:
— значение, равное 0 , при 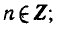
— наибольшее значение, равное 1, при 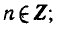
— наименьшее значение, равное — 1, при 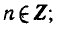
— положительные значения на интервале 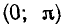
интервалах, получаемых сдвигами этого интервала на 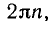
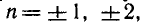
— отрицательные значения на интервале 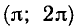
интервалах, получаемых сдвигами этого интервала
на 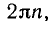
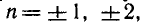
6) Функция у = sin х:
— возрастает на отрезке 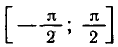
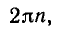
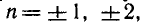
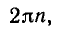
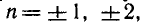
Задача:
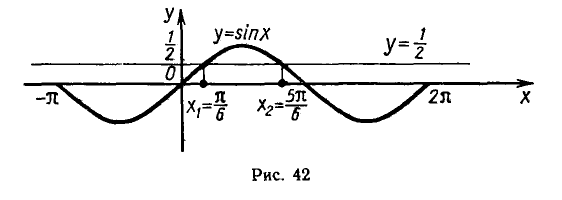
Найти все корни уравнения
принадлежащие отрезку
Построим графики функций у = sin х и 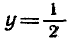
отрезке (рис. 42). Эти графики пересекаются в двух точках,
абсциссы которых являются корнями уравнения
На отрезке 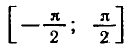
Второй корень 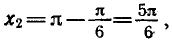
Ответ .
Задача:
Найти все решения неравенства
принадлежащие отрезку
Из рисунка 42 видно, что график функции y = sin x лежит
ниже графика функции 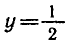
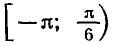
Ответ.
Функция y=tg x, ее свойства и график
Напомним, что функция y = tg x определена при 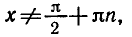
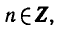
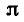
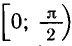
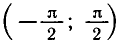
Наконец, используя периодичность, построить график функции
y = tgx на всей области определения.
Прежде чем строить график функции на промежутке 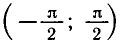
покажем, что на этом промежутке функция y = tg x возрастает.
Пусть 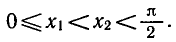
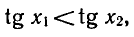
По условию 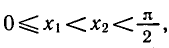
у = sin х, имеем 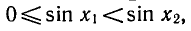
y = cos x имеем 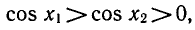
Перемножив неравенства 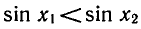
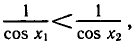
Используя свойство возрастания функции y = tg x на промежутке 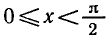
Пользуясь свойством нечетности функции y = tg x, отразим
построенный на промежутке 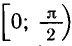
Напомним, что при 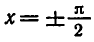
Если 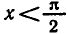
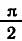
a cos х, оставаясь положительным, стремится к 0. При этом дробь 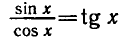
у = tg х приближается к вертикальной прямой 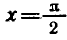
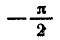
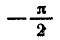
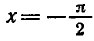
Перейдем к построению графика функции у = tg х на всей области определения. Функция y = tg х периодическая с периодом 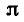
Следовательно, график этой функции получается из ее графика
на интервале 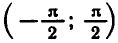
на 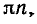
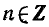
Итак, весь график функции у = tg х строится с помощью
геометрических преобразований его части, построенной на
промежутке 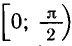
Поэтому свойства функции y = tg x можно получить, опираясь
на свойства этой функции на промежутке 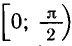
функция y = tg x возрастает на интервале 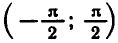
эта функция возрастает на промежутке 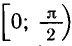
нечетной.
Перечислим основные свойства функции y = tg x:
1) Область определения — множество всех действительных
чисел
2) Множество значений — множество R всех действительных
чисел.
3) Функция у = tg х периодическая с периодом 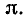
4) Функция y = tg x нечетная.
5) Функция у = tg x принимает:
— значение, равное 0, при 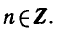
— положительные значения на интервалах 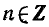
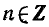
6) Функция у = tg х возрастает на интервалах
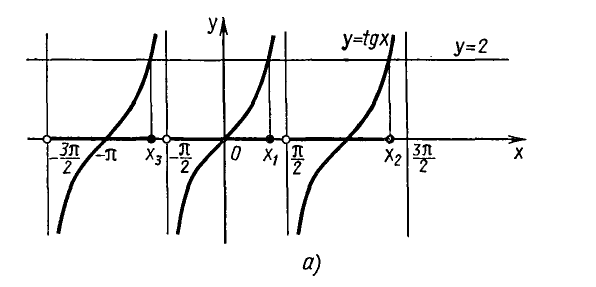
Задача:
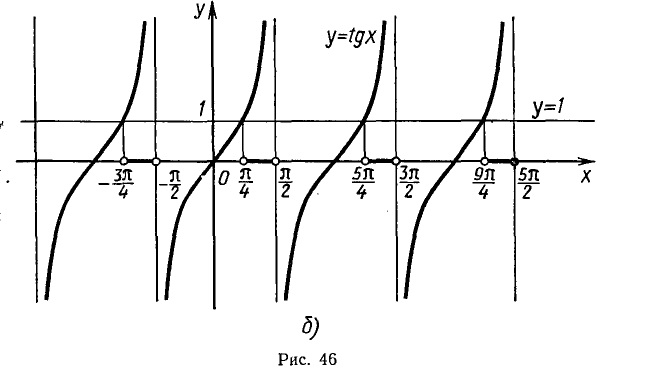
Найти все корни уравнения tg х = 2, принадлежащие отрезку
Построим графики функций y = tg х и у = 2 на данном отрезке (рис. 46, а) . Эти графики пересекаются в трех точках, абсциссы которых 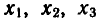
На интервале 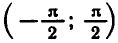
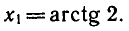
Так как функция у = tg х периодическая с периодом 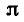
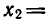
Ответ.
Задача:
Найти все решения неравенства
принадлежащие отрезку
Из рисунка 46, а видно, что график функции y = tg х лежит
не выше прямой у = 2 на промежутках
и 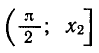
Ответ. 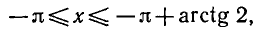
Задача:
Решить неравенство tg х > 1.
Построим графики функций y = tg x и у = 1 (рис. 46, б).
Рисунок показывает, что график функции y = tgx лежит выше
прямой у = 1 на промежутке 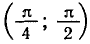
полученных сдвигами его на и т. д.
Ответ.
Тригонометрические функции широко применяются в математике, физике и технике. Например, многие процессы, такие, как колебание струны, колебание маятника, напряжение в цепи
переменного тока и т. д., описываются функцией, которая задается формулой 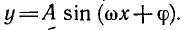
гармоническими колебаниями, а описывающие их функции —
гармониками (от греческого harmonikos — соразмерный). График
функции 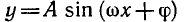
сжатием или растяжением ее вдоль координатных осей и
сдвигом вдоль оси Ох. Обычно гармоническое колебание является
функцией времени: 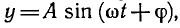
колебания, 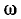
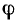
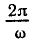
Видео:11 Преобразования графиков тригонометрических функцийСкачать

Углы и их измерение
Геометрический угол — это часть плоскости, ограниченная двумя лучами, выходящими из одной точки, вершины угла. Чтобы сравнивать углы, удобно закрепить их вершины в одной точке и вращать стороны.
Как измеряют углы? В качестве единицы измерения геометрических углов принят градус 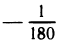
Конкретные углы удобно измерять в градусах с помощью транспортира. Многие оптические приборы также используют градусную меру угла. Углы, получающиеся при непрерывном вращении, удобно измерять не в градусах, а с помощью таких чисел, которые отражали бы сам процесс построения угла, т. е. вращение. На практике углы поворота зависят от времени, и поэтому удобно связать измерение углов со временем.
Представим себе, что зафиксирована не только вершина угла, но и один из образующих его лучей. Заставим второй луч вращаться вокруг вершины. Ясно, что получающиеся углы будут зависеть от скорости вращения и времени. Можно считать, что вращение происходит равномерно (с постоянной угловой скоростью). Тогда поворот будет определяться путем, который пройдет какая-либо фиксированная точка подвижного луча.
Если расстояние точки от вершины равно /?, то при вращении точка движется по окружности радиуса R. Отношение пройденного пути к радиусу R не зависит от радиуса и может быть взято за меру угла. Численно она равна пути, пройденному точкой по окружности единичного радиуса.
Итак, пусть угол получен вращением подвижного луча от некоторого начального положения. Его величина численно равна пути, который пройдет точка этого луча, находящаяся на единичном расстоянии от вершины.
Развернутый угол измеряется половиной длины единичной окружности. Это число обозначается буквой л. Число я было известно людям с глубокой древности и с довольно большой точностью. Первые десятичные знаки этого числа таковы:
π = 3,14159265358….
Угол величиной π часто используется как самостоятельная единица измерения углов — прямой угол равен 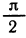
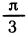
Часто встречаются записи меры углов в виде 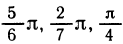
АННА ВОВК u715078663 ДЕЛАЕТ АЛГЕБРУ №2 (дополнительная)
Гаусс Карл Фридрих
(1777—1855) — немецкий математик, астроном и физик. Еще студентом написал «Арифметические исследования», определившие развитие теории чисел до нашего времени. В 19 лет определил, какие правильные многоугольники можно построить циркулем и линейкой. Занимался геодезией и вычислительной астрономией. Создал теорию кривых поверхностей. Один из создателей неевклидовой геометрии.
Так как на практике приходится иметь дело как с градусной, так и с радианной мерой, то на микрокалькуляторе обычно есть рычажок, регулирующий способ измерения используемого в вычислениях угла. Фактически микрокалькулятор умеет переводить градусы в радианы и обратно.
Выведем формулы для этого перевода. Достаточно сравнить меры одного и того же угла, например прямого:
Откуда
Обратно можно выразить единицу (т. е. один радиан) в градусной мере:
В географии, астрономии и других прикладных науках используют доли градуса — минуту и секунду. Минута — это 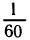
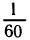
Заметим еще, что обозначение градуса (минуты, секунды) нельзя пропускать в записи, а обозначение радиана опускают. С физической точки зрения угол — безразмерная величина, поэтому имеют смысл записи: а = 0,23, а = 3,14, а=0,01. Во всех этих записях подразумевается, что угол а измерен в радианах. Подведем некоторые итоги. Угол мы можем получить вращением подвижного луча. Радианная мера угла численно равна пути, который проходит точка этого луча, отстоящая от вершины на расстояние 1.
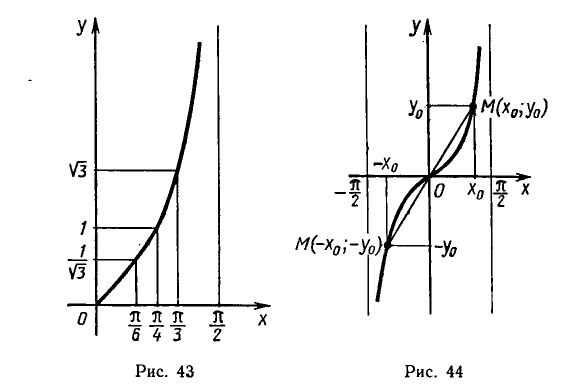
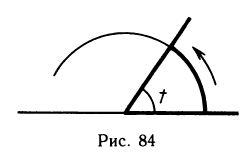
Движение точки по окружности во многом аналогично движению точки по прямой. Чтобы определить положение точки на прямой, недостаточно знать путь, пройденный ею от начальной точки, нужно указать еще направление движения. Обычно на прямой фиксируют положительное направление, а положение точки определяют одним числом, которое может быть не только положительным (как путь), но и отрицательным.
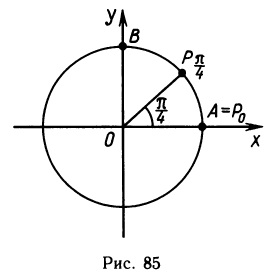
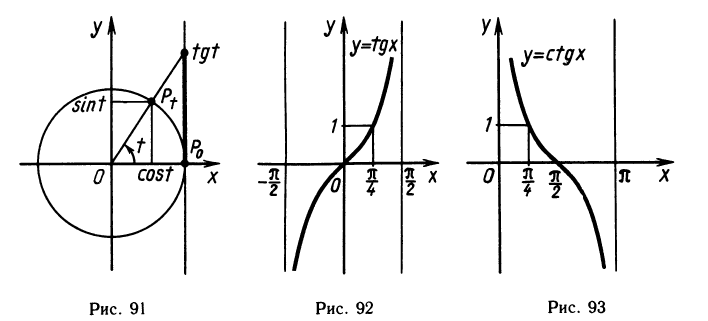
Аналогично поступают и с вращательным движением. В качестве положительного направления движения по окружности выбирается движение против часовой стрелки. Угол задают числом t (которое может принимать произвольное значение). Чтобы построить угол t, на единичной окружности от неподвижной точки откладывают путь, равный|t|, в направлении, определяемом знаком числа t. Таким образом, для произвольного числа t мы построили угол t, определяемый двумя лучами — неподвижным и тем, который проходит через построенную точку (рис. 84).
При таком обобщении понятия угла постепенно отходят от его геометрического образа как части плоскости, лежащей между двумя лучами. Фактически слово «угол» становится для нас синонимом слова «число». Угол t (т. е. произвольное число t) может выступать у нас в качестве аргумента тригонометрических функций. Изображать угол t нам будет удобно не в виде пары лучей, а в виде точки единичной окружности. Для этого мы подробно рассмотрим вращательное движение.
Вращательное движение и его свойства
Представим себе маленький шарик, который равномерно вращается по единичной окружности в положительном направлении (т. е. против часовой стрелки). Будем считать, что в момент времени t = О шарик находился в положении А и что за время t = 1 он проходит по окружности расстояние, равное 1. Половину окружности шарик проходит за время, равное π, а всю окружность — за время 2 π.
Обозначим через Pt точку на окружности, в которой шарик находится в момент времени t. Для того чтобы найти на окружности точку Рt надо отложить от точки Р0—А по окружности дугу длиной |t| в положительном направлении, если t>0, и в отрицательном направлении (т. е. по часовой стрелке), если t
2. Пусть 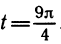
Заметим, что 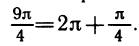
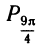
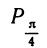
3. Найдем теперь точку 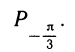
Таким образом, мы для каждого значения t можем построить точку Рt. На языке механики аргумент t — это время, на языке геометрии t — это угол.
Оси координат делят плоскость на четыре части. В зависимости от того, в какую часть плоскости попадает точка Рt, говорят о том, в какую четверть попадает угол t. При этом полезно помнить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла. Перечислим некоторые свойства вращательного движения.
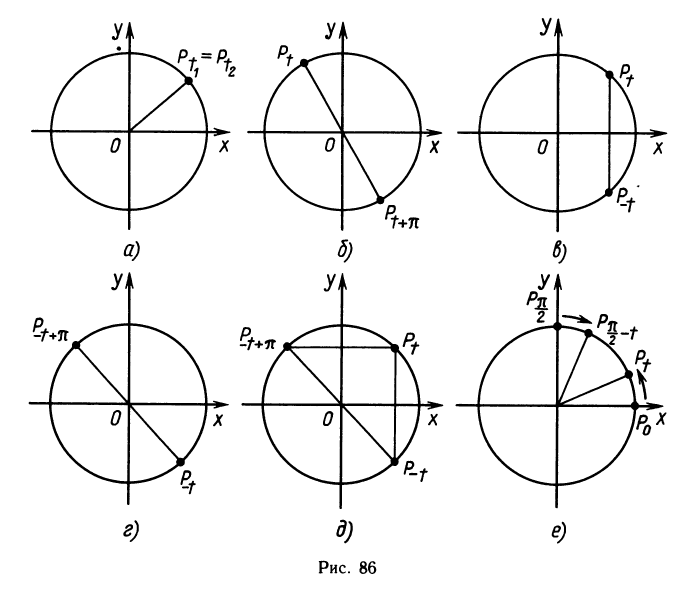
Свойство 1. Для всякого целого числа k точка Рt совпадает с точкой 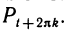
Свойство 2. Если 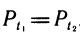
Свойство 3. Для всякого значения t точки Рt и Рt+π диаметрально противоположны.
Свойство 4. Для всякого значения t точки Рt и Р_t симметричны друг другу относительно оси абсцисс.
Свойство 5. Для всякого значения t точки Рt и Р_t+π симметричны относительно оси ординат.
Свойство 6. Для всякого значения t точки Рt и 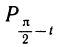
Эти свойства легко объяснить с помощью рисунка 86. Сделаем лишь пояснение к свойству 6. Возьмем две точки Р0 и
Они симметричны друг другу относительно биссектрисы первого и третьего координатных углов. Чтобы построить точку Рt, надо от точки Р0 двигаться в одном каком-то направлении на расстояние |t|, а чтобы построить точку 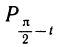
расстояние двигаться от точки 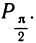
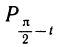
оставаться симметричными друг другу относительно указанной прямой.
Видео:Тригонометрические уравнения | Борис ТрушинСкачать

Определение тригонометрических функций
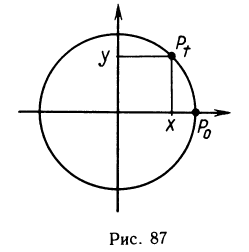
Тригонометрические функции определяются с помощью координат вращающейся точки. Рассмотрим на координатной плоскости ху единичную окружность, т. е. окружность единичного радиуса с центром в начале координат. Обозначим через Ро точку единичной окружности с координатами (1; 0) (рис. 87). Точку Ро будем называть начальной точкой. Возьмем произвольное число t. Повернем начальную точку на угол t. Получим точку на единичной окружности, которую обозначим через Рt.
Определение. Синусом числа t называется ордината точки Pt, косинусом числа t называется абсцисса точки Pt, где Р, получается поворотом начальной точки единичной окружности на угол t.
Если обозначить координаты точки Р, через х и у, то мы получим x = cost y = sint или можно записать, что точка Рt имеет координаты (cos t; sin t).
Так как координаты точки Р, (х; у), лежащей на единичной окружности, связаны соотношением х2 + у2 = 1, то sin t и cos t связаны соотношением
которое называют основным тригонометрическим тождеством.
Определение. Тангенсом числа t называется отношение синуса числа t к его косинусу, т. е. по определению
Котангенсом числа t называется отношение косинуса числа t к его синусу, т. е. по определению
Тангенс числа t определен для тех значений t, для которых cos t ≠ 0. Котангенс числа t определен для тех значений t, для которых sin t ≠ 0.
Периодичность
Тригонометрические функции являются периодическими функциями.
Число 2π является периодом синуса и косинуса.
Доказательство. Необходимо доказать тождества
Значения тригонометрических функций определяются с помощью координат вращающейся точки. Так как точки Pt и Рt+2π совпадают, то совпадают и их координаты, т. е. cos t = cos (t + 2π) и sin t = sin (t + 2π), что и требовалось доказать.
Действительно, 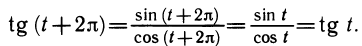
Равенство sin (t + 2π) = sin t верно при всех значениях t. Подставляем в это равенство вместо t число t+2π, получаем цепочку равенств sin(t+ 2 π +2 π ) = sin (t + 2 π ) = sin t, т. е. равенство sin (t + 4 π ) = sin t также верно при всех значениях t. Аналогично, подставляя вместо t число t— 2 π , получим тождество sin (t —2 π ) = sin t. Можно сказать так, что раз 2 π является периодом синуса, то и 2-2 π , —2 π также являются его периодами. Получаем, что всякое число вида 2πk <k ∈ Z) является периодом синуса.
Число 2π выделяется тем, что это наименьший положительный период синуса. Аналогично 2π — наименьший положительный период косинуса. У тангенса и котангенса наименьшим положительным периодом будет число π. Эти утверждения мы докажем позже.
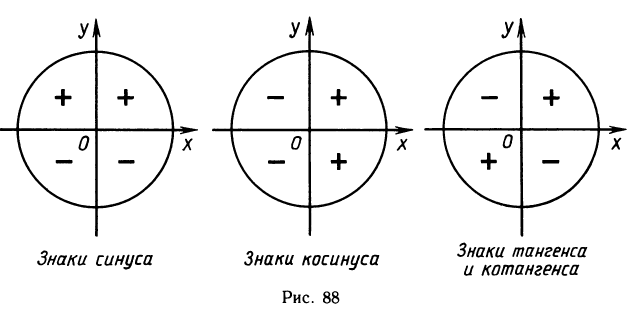
Знаки тригонометрических функций
Знаки тригонометрических функций определяются в зависимости от того, в какой четверти лежит рассматриваемый угол.
Синус числа t есть ордината точки Рt. Поэтому синус положителен в первой и второй четвертях и отрицателен в третьей и четвертой.
Косинус числа t как абсцисса точки Рt положителен в первой и четвертой четвертях и отрицателен во второй и третьей.
Тангенс и котангенс являются отношением координат. Поэтому они положительны тогда, когда эти координаты имеют одинаковые
знаки (первая и третья четверти), и отрицательны, когда разные (вторая и четвертая четверти). Знаки тригонометрических функций по четвертям приведены на рисунке 88.
Четность
Синус — нечетная функция, т. е. при всех t выполнено равенство sin (— t) = — sin t.
Косинус — четная функция, т. е. при всех t выполнено равенство cos ( — t) =cos t.
Действительно, мы знаем, что для всякого значения t точки Р, и Р_( симметричны друг другу относительно оси абсциссы (т. е. cos t = cos ( — t)), а ординаты противоположны (т. е. sin t=— sin ( — t)), что и требовалось доказать.
Следствие. Тангенс и котангенс — нечетные функции.
Действительно, 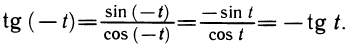
Формулы приведения
Значения тригонометрических функций острых углов можно вычислить по таблицам или с помощью прямоугольного треугольника. Их вычисление для любого значения аргумента можно привести к вычислению значений для аргумента
Соответствующие формулы так и называются — формулы приведения. Они основаны на симметрии вращательного движения.
Формула (1) —это запись в координатной форме свойства 3 вращательного движения, формула (2) — это запись свойства 5, а формула (3) — запись свойства 6.
С помощью периодичности и формул (1) — (3) можно привести вычисление синуса и косинуса любого числа t к их вычислению для t, лежащего между 0 и 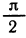
Из основных формул (1) — (3) можно вывести и другие формулы приведения:
Аналогично выводятся формулы
Формулы приведения для тангенса и котангенса получаются как следствие аналогичных формул для синуса и косинуса. Например:
Мнемоническое правило для запоминания формул приведения следующее:
1) Название функции не меняется, если к аргументу левой части добавляется — π или + π, и меняется, если добавляется число ± 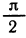
2) Знак правой части определяется знаком левой, считая, что
1.Вычислить sin 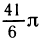
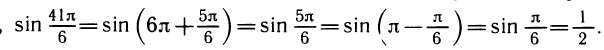
Значения тригонометрических функций
Вычисление значений тригонометрических функций имеет длинную историю. Потребности точных астрономических наблюдений вызвали к жизни появление огромных таблиц, позволявших производить вычисления с четырьмя, пятью и даже семью и более знаками. На составление этих таблиц было затрачено много усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем моментально получить требуемое значение с очень высокой точностью. С помощью большой вычислительной машины нетрудно найти, если нужно, значения тригонометрических функций с любой степенью точности.
Некоторые соображения о значениях тригонометрических функций надо помнить всегда, так как они облегчают вычисления.
1) С помощью формул приведения вычисление значения тригонометрической функции любого числа можно свести к вычислению функции угла, лежащего в первой четверти.
2) Достаточно знать значение лишь одной из тригонометрических функций. С помощью основных тождеств и зная четверть, в которой лежит значение аргумента, легко найти значения остальных функций.
Примеры:
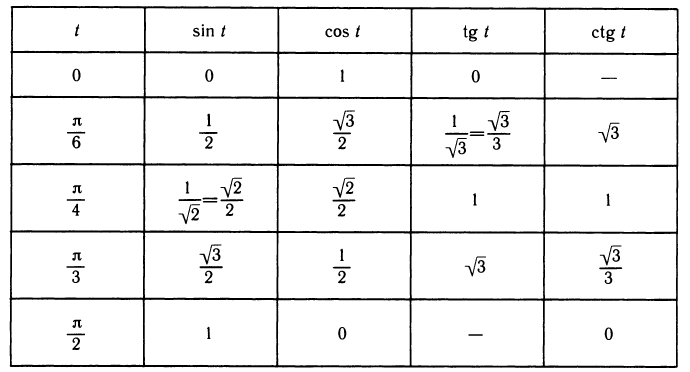
3) Полезно помнить значения тригонометрических функций для углов двух «знаменитых» прямоугольных треугольников —для равнобедренного и для треугольника с углами 30° (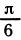
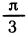
Сведем их в таблицу, дополнив ее значениями t = 0 и t=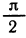
Решение простейших тригонометрических уравнений
Для решения некоторых,особенно простых, но важных уравнений достаточно вспомнить определение тригонометрической функции.
- sin t = 0. Вращающаяся точка Рt имеет нулевую ординату в моменты времени t—0, π, 2 π, …, а также t— π, —2 π…..В общем виде множество этих значений можно записать в виде t=πk, k ∈ Z. Таким образом, решением уравнения sin t = 0 будут числа t = πk, k ∈ Z.
Запишем кратко решения еще нескольких уравнений, правильность которых предлагается проверить самостоятельно.
Все рассмотренные уравнения имеют бесчисленное множество решений. Эти решения записываются в виде бесконечных серий с помощью переменной (в наших примерах к), которая может принимать любые целые значения.
Теперь легко доказать, что 2π является наименьшим положительным периодом синуса и косинуса. Действительно, формула 3 показывает, что значение 1 синус принимает только в точках
Расстояние между соседними точками этой последовательности равно 2 π, поэтому синус не может иметь положительный период, меньший 2 π. Рассуждения для косинуса аналогичны.
Видео:#2. Как решать тригонометрические уравнения? 3 способа!Скачать

Исследование тригонометрических функций
Основные свойства синуса и косинуса
При введении тригонометрических функций мы обозначали аргумент буквой t, так как буквы х и у были заняты — они обозначали координаты вращающейся точки Рt. Сейчас при исследовании мы вернемся к обычным обозначениям: х — аргумент, у — функция.
Рассмотрим функции y = sinx и y = cosx.
1) Область определения. Синус и косинус числа х задаются как координаты точки Рх, получающейся из точки Ро (1; 0) поворотом на угол х. Так как поворот возможен на любой угол, то областью определения синуса и косинуса является множество R всех вещественных чисел.
2) Промежутки монотонности. Проследим за характером изменения координат точки Рх, движущейся по окружности. При х = 0 точка занимает положение Ро (1; 0). Пока она движется по окружности, оставаясь в первой четверти, ее абсцисса уменьшается, а ордината увеличивается. При x= 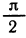
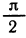
Когда точка переходит во вторую четверть, ордината начинает убывать от 1 до 0. Абсцисса становится отрицательной и растет по абсолютной величине, значит, косинус продолжает убывать от 0 до — 1. В третьей четверти синус становится отрицательным и убывает от 0 до —1, а косинус начинает возрастать от — 1 до 0.
Наконец, в четвертой четверти синус возрастает от — 1 до 0 и косинус возрастает от 0 до 1. Монотонность синуса и косинуса по четвертям показана на схеме VIII.
3) Точки экстремума. Координаты вращающейся точки меняются между —1 и +1. Эти числа являются наименьшими и наибольшими значениями синуса и косинуса. Если требуется указать абсциссы точек экстремума, то надо решить уравнения sin х = ±1 и cos х= ± 1.
4) Промежутки постоянного знака и корни функции. Мы повторим их еще раз при построении графика.
5) Множество значений. Синус и косинус принимают любые значения от —1 до +1, так как являются координатами точки, движущейся по единичной окружности.
Графики синуса и косинуса
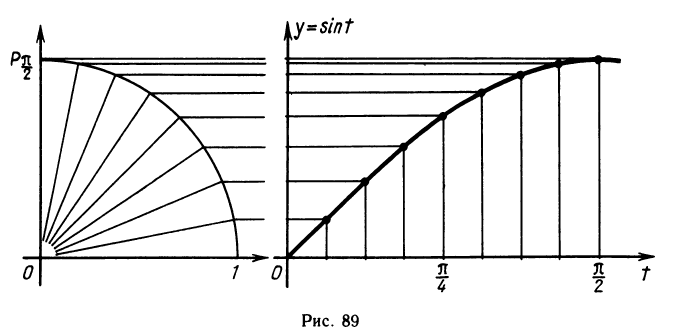
Для приближенного построения синусоиды можно поступить так. Разделим первую четверть на 8 равных частей и на столько же частей разделим отрезок [0; 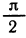
Так мы получим график синуса на промежутке [0;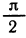
как sin (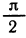
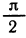
симметричен относительно прямой x=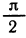
график синуса на отрезке [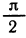
синуса, получим график синуса на отрезке [ — π; 0] симметричным отражением построенной части синусоиды относительно начала координат. Так как отрезок [— π; π] имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельными переносами построенной кривой.
График синуса мы построили, воспользовавшись его свойствами. При этом к определению синуса мы обращались только при построении графика на отрезке [0; 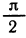
Построение графика на всей оси потребовало знания симметрии вращательного движения (формулы приведения, нечетность, периодичность). После того как график построен, полезно вернуться к свойствам синуса и посмотреть, как они проявляются на графике.
Функция y = sin х имеет период 2 π. На графике это свойство отражается следующим образом: если мы разобъем ось х на отрезки длиной 2 π, например, точками… —4 π, —2 π, 0, 2 π, 4 π, …, то весь график разобьется на «одинаковые» части, получающиеся друг из друга параллельным переносом вдоль-оси х. При этом видно, что 2 π — наименьший положительный период синуса.
Функция y = sin x: нечетна. На графике это свойство проявляется так: синусоида симметрична относительно начала координат.
Функция y = sin x обращается в нуль при х = πk, k ∈ Z. На графике это точки пересечения синусоиды с осью абсцисс.
Функция y = sin x положительна при 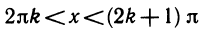
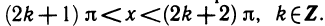
Указанные отрезки соответствуют четвертой-первой и второй-третьей четвертям.
Множеством значений функции y = sinx является отрезок [— 1; 1]. Действительно, проекции вращающейся точки на ось заполняют отрезок [—1; 1]. На графике это свойство проявляется так: синусоида расположена в полосе 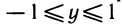
График косинуса можно построить так же, как и график синуса. Возможен и другой путь. Формулы приведения показывают, что синус и косинус связаны между собой простыми соотношения-
ми. Воспользуемся, например, формулой cosx = sin (x+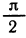
Эта формула показывает, что график косинуса получается сдвигом синусоиды на 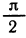
Если изображать графики синуса и-косинуса в системе координат с одинаковым масштабом по осям, то синусоида получается очень растянутой. Однако на практике величины х и у, связанные с помощью тригонометрических функций, имеют различные единицы измерения и необязательно изображать их в одном масштабе.
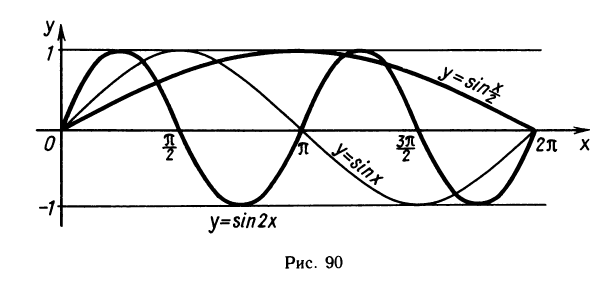
Если аргумент умножить на некоторое число, то синусоида будет, как гармоника, сжиматься и растягиваться по оси х. Примеры такого преобразования приведены на рисунке 90.
Если значение синуса умножить на число, то будет происходить растяжение (сжатие) по оси у.
Графики функций вида у = А sin ( ω х + а) при различных А, ω, а являются синусоидами. Эти функции описывают так называемые гармонические колебания — движение проекции вращающегося шарика на ось или колебания конца упругой пружины.
Постоянные величины А, ω, а, задающие колебания, имеют наглядный физический смысл: А — амплитуда колебания, ω — его частота, а — начальная фаза.
Исследование тангенса и котангенса
Если свойства синуса и косинуса мы получили, рассматривая свойства движения точки по окружности, то для исследования тангенса и котангенса нам нет необходимости возвращаться к механической модели.
По определению тангенс числа х задается как отношение sin х и cos х. Изучим свойства тангенса.
1.Областью определения функции 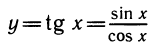
множество всех вещественных чисел, за исключением тех, в которых косинус обращается в нуль. Мы запишем это множество следующим образом:
2. Тангенс — периодическая функция с периодом π:
3. Тангенс — нечетная функция, т. е. tg ( — х)= — tg х.
4. Функция y = tg x обращается в нуль одновременно с синусом, т. е. при x=πk, k ∈ Z.
5. Функция у= tg x: положительна в первой и третьей четвертях и отрицательна во второй и четвертой.
Выберем для дальнейшего изучения тангенса какой-либо промежуток числовой оси длиной, равной периоду, т. е. числу π. Можно было бы выбрать отрезок от 0 до π, но это неудобно, так как внутри этого отрезка есть точка x= 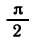
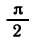
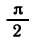
6. Тангенс возрастает в первой четверти. Действительно, пусть
Тогда 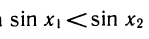
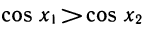
Умножим это неравенство на неравенство с положительными членами: sin х1
На промежутке (—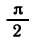
В итоге тангенс возрастает на промежутке (-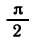
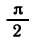
7. Какие же значения принимает тангенс? Когда х возрастает от 0 до 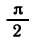
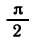
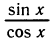
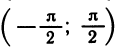
Мы показали, что областью значений тангенса является вся числовая ось R.
Вообще на этой оси, которую часто называют осью тангенсов, можно проследить все свойства тангенса.
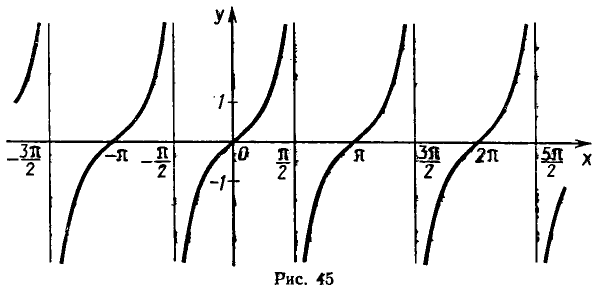
8. Построим график тангенса. На промежутке 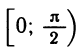
тангенса можно построить по точкам, учтя, что тангенс строго возрастает, в нуле обращаясь в нуль, а при приближении к 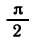
Отразив построенную часть графика относительно начала координат (тангенс — нечетная функция), получим график тангенса на промежутке 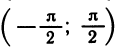
разобьем числовую ось на отрезки, перенося 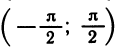
и влево на π, 2 π, З π и т. д.
График тангенса распадается на отдельные, не связанные между собой части. Это вызвано тем, что в точках 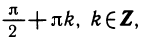
Замечание (о монотонности тангенса).
Мы доказали, что функция тангенс возрастает на 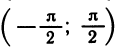
Можно ли сказать, что тангенс возрастает на всей области определения? Нет. Достаточно посмотреть на график. Если взять
Нарушение монотонности связано с тем, что между точками х1 и х2 лежала точка х = 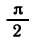
Однако можно сказать, что тангенс возрастает на каждом промежутке, который целиком попадает в его область определения.
Свойства котангенса получаются так же, как и свойства тангенса. Перечислим кратко эти свойства, оставляя их доказательство для самостоятельной работы.
1.Функция 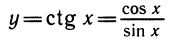
2. Функция у = ctg х периодична. Ее периодом является число π:
3. Функция у = ctg x нечетна: ctg ( — х)= — ctg х.
4. Функция у = ctg х обращается в нуль одновременно с косинусом, т. е. при х = 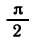
5. Функция у = ctgx: положительна в первой и третьей четвертях и отрицательна во второй и четвертой.
6. Функция y=ctgx убывает на промежутке (0; π). Перенося его на kπ, получаем, что котангенс убывает на каждом промежутке ( πk; π + πk).
7. Область значений котангенса — множество R всех вещественных чисел.
8. График котангенса изображен на рисунке 93.
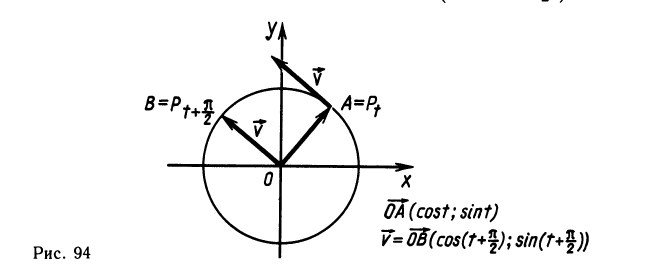
Производные тригонометрических функций
Пусть точка А движется с единичной скоростью . по окружности радиуса 1 с центром в начале координат О в положительном направлении. Координаты точки А в момент времени t равны cos t и sin t. Вектор мгновенной скорости точки А в момент времени t направлен по касательной к окружности в точке А (рис. 94), и в силу теоремы о перпендикулярности касательной к радиусу, проведенному в точку касания, вектор 
Вычислим координаты вектора 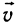
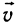
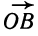
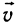
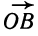
Вектор 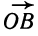
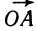
то 
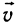
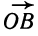
С другой стороны, координаты скорости 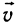
Найдем производную функции y = A sin ( ωt + а):
Вычислим теперь производную функции y = tgx. Так как 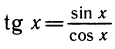
Примеры:
Приближенные формулы
Главная приближенная формула: вблизи нуля sin t ≈ t.
Доказательство. Дифференциал функции y = sin х равен dy = cos х dx. Найдем dy при х = 0. Так как cos 0=1, то при х = 0 dy = dx. Найдем приращение функции:
∆y = sin ∆х — sin 0 = sin ∆х.
Так как ∆y ≈ dy, то получим ∆y = sin ∆х ≈ dy=dx = ∆х. Вместо ∆х можно написать t и получить sin t ≈ t.
Эта формула дает тем точнее значение синуса, чем ближе t к нулю. Возможность заменять sin t на t при маленьких значениях угла t широко употребляется в приближенных вычислениях. Можно дать различные интерпретации этой приближенной формулы.
1. 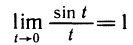
функции к его главной части стремится к единице при стремлении к нулю приращения аргумента.
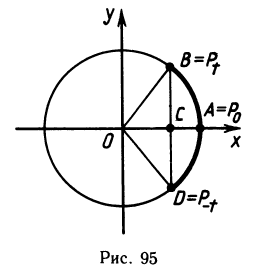
2. Рассмотрим единичный круг. Пусть для простоты t>0. Тогда длина дуги АВ равна t, а длина отрезка ВС равна sin t. Удвоим дугу АВ и отрезок ВС — дуга BD имеет длину 2t, а хорда BD — длину 2 sin t. Соотношение sin t ≈ t означает, что отношение длины хорды к длине стягиваемой ею дуги стремится к единице, когда дуга стягивается в точку (рис. 95).
3. Рассмотрим касательную к синусоиде в начале координат. Так как (sin x)’=cos х, a cos 0= 1, то уравнение этой касательной у — х. Таким образом, заменяя вблизи начала координат график синуса отрезком касательной, мы вычисляем приближенное значение синуса по формуле sin t ≈ t.
Для получения других приближенных формул выпишем дифференциалы тангенса и косинуса:
При x = 0 получим приближенное значение тангенса:
Применяя этот же прием к косинусу, мы получим, что дифференциал косинуса при x=0 равен —sin0 • dx т. е. равен 0. Это означает, что главная часть приращения косинуса равна нулю и в первом приближении cos x ≈ cos 0 = 1. Можно получить более точную формулу таким путем. Запишем cos х так:
Заменим в этой формуле sin х на х и воспользуемся приближенной формулой для квадратного корня:
Полученная приближенная формула для косинуса вблизи точки x = 0 весьма точна.
Более точные приближения можно получить с помощью формул
Примеры:
- Вычислить приближенно sin 0,03 • tg 0,12. sin 0,03 ≈ 0,03, tg 0,12 ≈ 0,12, sin 0,03 • tg 0,12 ≈ 0,0036 ≈ 0,004.
- Вычислить приближенно sin 2°. Переводим 2° в радианную меру: 2° ≈ 0,034. sin 2° ≈ 0,034.
Видео:Построение графиков тригонометрических функцийСкачать

Тождественные преобразования
Формулы сложения
Тригонометрические функции связаны между собой многочисленными соотношениями. Первая серия тождеств описывает связь между координатами точки окружности — это так называемые основные соотношения. Эти соотношения позволяют выразить значения одних функций через другие (при одном и том же значении аргумента). Вторая серия тождеств происходит от симметрии и периодичности в движении точки по окружности. Отсюда мы получаем формулы приведения. Третий источник тригонометрических формул — это изучение поворотов. Поворот точки на угол а + β можно составить из композиции двух поворотов — на угол а и на угол β. Есть простые формулы, связывающие координаты точек 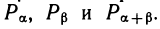
Нашей целью является вывод формул, связывающих sin (а ± β), cos (а ± β), tg (а ± β), ctg (а ± β) с тригонометрическими функциями углов а и β. Достаточно вывести формулу косинуса разности, остальные формулы получатся как ее следствия.
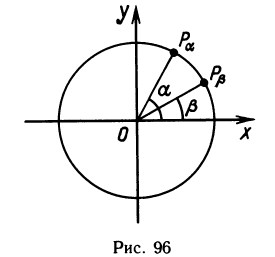
Теорема. Косинус разности двух углов равен произведению косинусов этих углов, сложенному с произведением синусов:
cos (а — β) =cos а cos β + sin а sin β.
Доказательство. Построим углы а и β помощью единичной окружности, т. е. точки Ра и Рβ , такие, что векторы 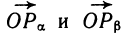
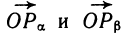
Вычислим скалярное произведение этих векторов. По определению скалярного произведения
(так как векторы 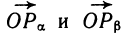
Теперь вычислим это же скалярное произведение с помощью координат:
Сравнивая результаты вычислений, получаем требуемую формулу:
Доказательство теоремы закончено. Выведем остальные формулы.
Косинус суммы. Сумму а + β представим как разность а — ( — β) и подставим в формулу для косинуса разности:
Воспользуемся тем, что cos( —p) = cos p (четность косинуса), a sin( —p)=—sin p (нечетность синуса). Получим:
Синус суммы. Воспользуемся одной из формул приведения:
Теперь по формуле косинуса разности получим:
В качестве примера вычислим sin 15°. Представим 15° как разность 45° —30°. Получим sin 15° = sin (45° — 30°) = sin 45° cos 30°
Тангенс суммы и разности. По определению tg(a + β) 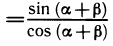
Разделив числитель и знаменатель этой дроби на cos a cos β, получим:
Заменяя β на ( — β) и пользуясь нечетностью тангенса, получаем:
Формулы удвоения
Формулы сложения являются одними из основных формул, связывающих тригонометрические функции. Из них можно вывести различные следствия. Полагая а = р, получим так называемые формулы удвоения.
Заметим, что в формуле для cos 2a можно заменить 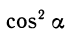
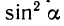
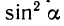
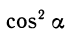
Тригонометрические функции половинного угла
Из формул двойных углов 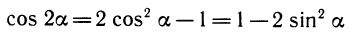
Затем в этих формулах подставив 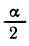
Извлекая корень, получим:
(Для того чтобы раскрыть модули, надо знать, в какой четверти лежит угол 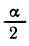
Обилие тригонометрических формул связано с тем, что между основными тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом — есть соотношения, которые позволяют по-разному написать одно и то же выражение. Возникает вопрос: нельзя ли выбрать одну какую-то функцию и через нее выражать все остальные? Если в качестве такой функции мы выберем синус, то во многих формулах появятся квадратные корни. Так, например, выражая sin 2а через sin а, мы получим sin 2а = 2 sin а cos а = 2 sin а 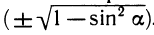
Оказывается, что все тригонометрические функции от аргумента х (и от nх при целом n) выражаются через тангенс угла 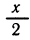
Напишем формулы двойного угла для исходного угла
Представим число 1 в виде 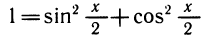
Поделим теперь числитель и знаменатель каждой дроби на
Пользуясь этими формулами, можно функцию вида у = а sin x + b cos x + c представить в виде рациональной функции от tg 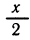
Пример. Выразить у = 2 sin х + З cos х — 1 в виде функции от tg 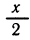
Преобразование суммы тригонометрических функций в произведение и обратные преобразования
Пусть требуется преобразовать сумму sin a + sin β в произведение. Используем следующий искусственный прием: напишем тождества
заменим а и β выражениями, стоящими справа, в формулах для синуса суммы и разности:
Аналогично выводятся еще три формулы:
Выпишем подряд четыре формулы сложения:
Вычитая почленно из четвертого равенства третье, получим:
Складывая третье и четвертое равенства, получим:
Складывая два первых равенства, получим:
Мы рассмотрели различные тождества, связывающие тригонометрические функции. Все их запомнить трудно, и приходится обращаться к таблицам и справочникам. Важнее запомнить не сами формулы, а то, какие функции между собой они связывают, что с их помощью можно получить.
Видео:Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Тригонометрические уравнения
Простейшим тригонометрическим уравнением называется уравнение вида sinx=a, где cos x=a, tgx=a, где a — некоторое действительное число.
Арксинус
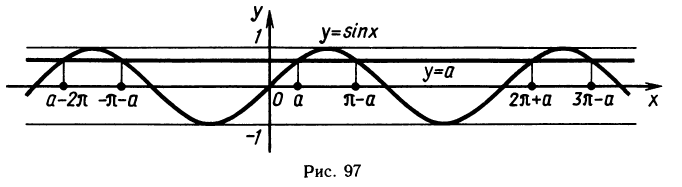
Рассмотрим уравнение sin x = a. Так как областью значений синуса является отрезок [—1; 1], то это уравнение не имеет решений при |a| > 1. Пусть теперь |а|
По рисунку ясно, что прямая у = а пересечет синусоиду бесконечно много раз. Это означает, что при |a| ≤ 1 уравнение sin x = a имеет бесконечно много корней. Так как синус имеет период 2π, то достаточно найти все решения в пределах одного периода. По графику видно, что при |a|
Эти две серии решений иногда записываются одной формулой:
Пример. Решить уравнение
Одно решение этого уравнения 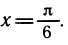
Как мы уже выяснили, уравнение sinx=a при |а| ≤ 1 имеет бесконечно много решений. Для одного из них имеется специальное название — арксинус.
Определение. Пусть число а по модулю не превосходит единицы. Арксинусом числа а называется угол х, лежащий в пределах от 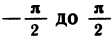
Обозначение: х = arcsin а.
Итак, равенство x = arcsin a равносильно двум условиям: sin z = a и
Обратим еще раз внимание на то, что arcsin а существует лишь, если |а|≤ 1.
Примеры:
Теперь решения уравнения sin х = а (при |а| ≤ 1) можно записать так: х = arcsin а+2πk, х= π — arcsin а+2πk, или в виде одной формулы:
Запишем некоторые тождества для арксинуса.
- sin arcsin а = а.
Это тождество вытекает из определения арксинуса (arcsin а — это такой угол х, что sin х=а).
Действительно, обозначим sin х через а. Тогда наше тождество будет равносильно определению арксинуса: arcsin а = х, если 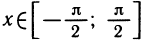
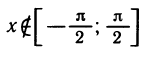
Действительно, синусы от правой и левой частей равны: sin (arcsin ( —а)) = —а и sin ( — arcsin а)= —sin (arcsin а)= —а. В то же время правая часть доказываемого равенства — это угол, принадлежащий отрезку 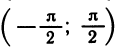
Арккосинус
Так же как и в предыдущем пункте, при |а|>1 уравнение cosx = a решений не имеет; если |а| ≤ 1 то решений уравнения бесконечно много.
Если a — какое-либо решение уравнения cos х=а, то —а также есть решение этого уравнения, так как cos a = cos ( — a). По графику или на единичном круге видно, что при |а|
Эти серии обычно записывают в виде одной формулы:
Пример. Решить уравнение
Одно решение находится легко: 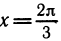
Запишем все решения так:
Так же как и для синуса, выделяется одно определенное решение уравнения cos х = а и ему дается специальное название — арккосинус.
Определение. Пусть а — число, по модулю не превосходящее единицы. Арккосинусом числа а называется угол х, лежащий в пределах от 0 до π, косинус которого равен а.
Обозначение: х= arccos а.
Равенство x = arccos a равносильно двум условиям: cos x = a и 0 ≤ х ≤ π. Арккосинус числа а существует лишь при |а| ≤ 1 .
Пример:
Решение уравнения cos х=а (при |а| ≤ 1) можно записать теперь в общем виде:
По каким причинам для значений арксинуса был выбран отрезок 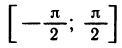
Это объясняется тем, что на этих отрезках, во-первых, синус и косинус принимают все возможные значения от — 1 до 1 и, во-вторых, каждое значение принимается ровно один раз. Отрезков с этими условиями бесконечно много, но при этом выбраны отрезки «поближе к нулю».
Для арккосинуса можно вывести ряд тождеств.
- cos (arccos а) = а.
Это тождество следует из определения арккосинуса.
Обозначим cos x = а. Получим определение арккосинуса: arccos а = х, если x ∈ [0; π ] и cos х = а.
Сначала вычислим косинус от левой и правой частей:
Если равны косинусы двух чисел, то это еще не означает, что равны сами числа. Проверим, что правая часть принадлежит отрезку [0; π]. (Так как левая часть тоже принадлежит этому отрезку, то из равенства косинусов двух чисел теперь уже будет следовать равенство самих чисел.) Итак, надо доказать, что π —arccos а принадлежит [0; π]. Действительно, arccos а ∈ [0; π — arccos а ∈ [ — π ; 0], π— arccos а ∈ [0; π], что и требовалось доказать.
Арктангенс
Область значений тангенса (котангенса) — вся числовая ось. Поэтому уравнения tgx = a, ctg х — а имеют решения при любом а. В пределах одного периода π тангенс и котангенс принимают каждое значение ровно один раз. Поэтому если известно одно решение уравнения tg х—а или ctg х=а, то все остальные получают прибавлением периода:
где a — какое-либо решение соответствующего уравнения. Примеры. Решить уравнения:
Определения арктангенса и арккотангенса вводятся аналогично определениям арксинуса и арккосинуса, поэтому мы проведем его короче.
Определение. Арктангенсом числа а называется угол 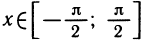
Обозначения: х = arctg а и x = arcctg а. Примеры.
2. Решить уравнения:
Решение тригонометрических уравнений
Тригонометрические уравнения встречаются в задачах, в которых из соотношений между тригонометрическими функциями требуется найти неизвестные углы. Основными, чаще всего встречающимися тригонометрическими уравнениями являются уравнения простейшего типа sin х — а, cos х = а, tg х = а и ctg х = а, которые уже рассмотрены в предыдущих пунктах. Следует отметить, что такие уравнения обычно имеют бесконечные серии решений, задаваемые с помощью параметра, принимающего целые значения.
Более сложные тригонометрические уравнения обычно решаются сведением их к простейшим с помощью различных алгебраических и тригонометрических формул и преобразований. Рассмотрим некоторые приемы решения тригонометрических уравнений.
а) Уравнения, алгебраические относительно одной из тригонометрических функций.
Примеры решения уравнений.
Это уравнение является квадратным относительно sin х. Корни этого квадратного уравнения 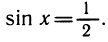
Если в уравнении встречаются разные тригонометрические функции, то надо пытаться заменить их все через какую-нибудь одну, используя тригонометрические тождества.
Так как квадрат синуса легко выражается через косинус, то, заменяя sin2 х на 1 —cos2 х и приводя уравнение к квадратному относительно cos х, получим 2 (1 —cos2 х) — 5 cos х — 5 = 0, т. е. квадратное уравнение 2 cos2 x + 5 cos x + 3 = 0, корни которого
Уравнение 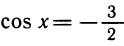
Заменив ctg x на 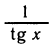
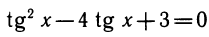
Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то получим уравнение с радикалами. Чтобы избежать этого, используют формулы, выражающие синус и косинус через тангенс половинного угла, т. е.
Делая замену, получаем уравнение относительно
Квадратное уравнение 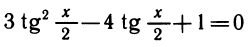
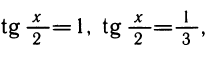
б) Уравнения, решаемые понижением их порядка.
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменить линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.
Примеры решения уравнений.
- Решить уравнение
Можно заменить cos 2х на 2 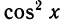
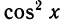
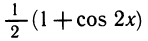
2. Решить уравнение
Подставляя вместо 
в) Уравнения, решаемые после преобразований с помощью тригонометрических формул.
Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы преобразования суммы в произведение.
Примеры решения уравнений.
Преобразуем произведение синусов в сумму:
Полученное уравнение можно решить разными способами. Можно воспользоваться формулами сложения и преобразовать в произведение. Удобнее воспользоваться условием равенства косинусов двух углов 2х и 6х:
Получим два уравнения:
Проверьте, что решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче:
г) Однородные уравнения.
Решим уравнение
Если считать, что sin х и cos х — члены первой степени, то каждое слагаемое имеет вторую степень. Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решать делением на старшую степень синуса (или косинуса). Делим наше уравнение на cos2 х. (При этом мы не потеряем корней, так как если мы в данное уравнение подставим cos x = 0, то получим, что и sin x=0, что невозможно.)
Гармонические колебания
Гармонические колебания — это процесс, который может быть описан функцией вида у = A sin (ω + а).
Примеры:
1) Колебания упругой пружины. Конец упругой пружины (точка Р) при ее сжатии или растяжении описывает колебательные движения. Если на прямой, по которой движется точка Р, ввести координату х так, чтобы в положении равновесия xр = 0, оттянуть конец пружины в положительном направлении на расстояние A и в момент времени t = 0 отпустить его, то зависимость координаты точки Р от времени t (рис. 98) будет иметь следуюший вид: 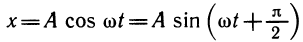
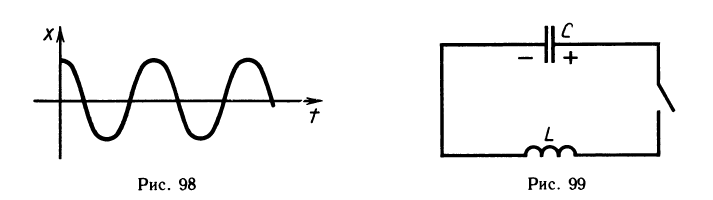
2) Электрический колебательный контур. Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора С и катушки индуктивности L (рис. 99). Если эту цепь замкнуть накоротко и считать, что в ней есть некоторый запас энергии (например, ненулевой заряд в конденсаторе), то по этой цепи пойдет ток, напряжение которого U будет меняться со временем. При идеальном предположении отсутствия потерь в цепи зависимость U от времени t будет иметь следующий вид: U = U0 sin (ωt + a), где ω — некоторая характеристика контура, которая вычисляется через параметры конденсатора и катушки. Константы Uo и а зависят от состояния цепи в начальный момент времени.
Таким образом, гармоническое колебание у=А sin (ωt + a) определяется тремя параметрами: амплитудой A>0, угловой скоростью ω>0 и так называемой начальной фазой а. Часто вместо угловой скорости ω говорят о частоте колебаний v, которая связана с угловой скоростью ω (или иначе круговой частотой) формулой ω = 2πv. Функция у периодична. Ее основной период равен
Колебания приходится складывать. В механике это связано с тем, что на точку может действовать несколько сил, каждая из которых вызывает гармонические колебания. В электро-и радиотехнике сложение колебаний происходит как естественное наложение токов. Оказывается, имеет место замечательный закон: при сложении гармонических колебаний одной и той же частоты получается снова гармоническое колебание той же частоты. На математическом языке это означает, что сумма двух функций
есть функция того же вида:
Достаточно научиться складывать функции вида у = A1 sin ωt и
y = A2 cos ωt. Для их сложения применяется прием введения вспомогательного угла. Итак, рассмотрим выражение у = A1 sin ωt + A2 cos ωt. Оно похоже на формулу синуса суммы: sin (ωt + a) = sin ωt cos a+ cos ωt sin a. Числа A1 и A2 нельзя считать косинусом и синусом, однако если их разделить на число 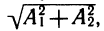
Примеры:
Периодические функции
Тригонометрические функции являются периодическими. В общем виде функция y = f(x) называется периодической, если существует такое число Т ≠ О, что равенство f (x+T)=f (х) выполняется тождественно при всех значениях х.
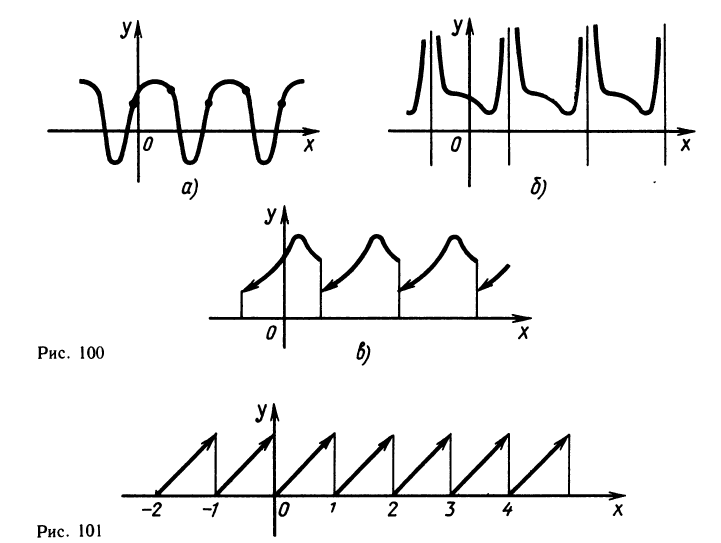
Обычно среди периодов периодической функции можно выделить наименьший положительный период, который часто называют основным периодом. Все другие периоды функции являются целыми кратными основного. График периодической функции состоит из повторяющихся кусков, поэтому достаточно построить его на отрезке изменения аргумента длиной, равной основному периоду. На рисунке 100 изображены графики различных периодических функций.
Приведем пример одной интересной периодической функции. Всякое число х можно представить в виде суммы его целой и дробной частей. Целая часть числа х определяется как наибольшее целое число, не превосходящее х, и обозначается [х]. Например, [3]=3; [3,14]=3; [ — 3,14]=— 4. Дробная часть обозначается и равна по определению x — [x]. Функция у — <х)=х — [х] является периодической с основным периодом, равным единице. Ее график изображен на рисунке 101.
Если функция y — f (х) периодична и ее периодом является число Т, то и функция y=f (kx) будет периодической, причем ее пе-риодом будет число 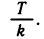
Сдвиг аргумента не меняет период функции. Отсюда следует, что функция у=А sin (ωt + а), задающая гармоническое колебание, имеет период
Если Т является общим периодом двух функций f и g, то Т остается периодом их суммы, произведения, частного. Правда, как мы видим на примере тангенса, если Т является основным периодом f и g, то это может быть не так для новых функций, полученных из f и g арифметическими операциями.
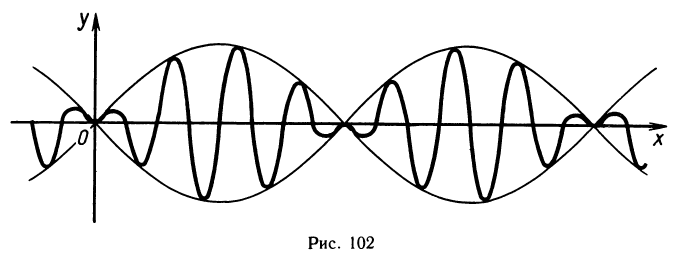
Сумма двух функций с различными периодами необязательно будет периодической. Интересен случай сложения двух функций с различными, но очень близкими периодами. Рассмотрим, например, сумму функций 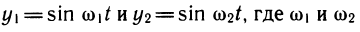
Поэтому 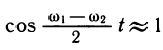
Однако с ростом t множитель 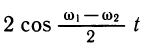
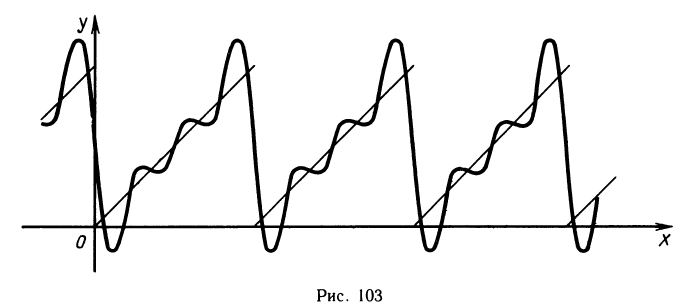
«Ровное» гармоническое колебание типа у1 заменится «биением», график которого изображен на рисунке 102. Можно представить себе, что «биение» — это колебание, амплитуда которого медленно (и тоже периодически) меняется. Явление «биения» можно наблюдать при наложении звуков близкой частоты, при измерении величины океанских приливов, которые вызываются наложением двух периодических процессов с близкими, но различными периодами — притяжением Солнца и притяжением Луны.
Разложение на гармоники
Чистый звуковой тон представляет собой колебание с некоторой постоянной частотой. Музыка, которую мы слышим, представляет собой наложение различных чистых тонов, т. е. получается сложением колебаний с различными частотами. Преобладание звука той или иной частоты (скажем, низких звуков или высоких) связано с амплитудой соответствующих колебаний. Это знакомое нам разложение звуков на чистые тона часто встречается при изучении различных колебательных процессов.
Можно сказать так: простейшие гармонические колебания являются теми кирпичиками, из которых складывается любое колебание. На языке математики это означает, что любую периодическую функцию можно представить с наперед заданной точностью как сумму синусов.
Эйлер Леонард
(1707—1783) — швейцарский математик и механик, академик Петербургской Академии наук, автор огромного количества научных открытий во всех областях математики. Эйлер первым применил средства математического анализа в теории чисел, положил начало топологии.
«Математика, вероятно, никогда не достигла бы такой высокой степени совершенства, если бы древние не приложили столько усилий для изучения вопросов, которыми сегодня многие пренебрегают из-за их мнимой бесплодности».
Л. Эйлер
Этот замечательный факт обнаружен еще в XVIII в. Д. Бернулли при решении задачи о колебании струны. Это показалось удивительным и невозможным по отношению к любой функции даже такому гениальному математику, как Л. Эйлер, который, кстати, является автором всей современной символики тригонометрии. Систематически разложения периодических функций в сумму синусов (или, как говорят, на гармоники) изучал в начале XIX в. французский математик Ж. Фурье, которые так теперь и называются разложениями (или рядами) Фурье.
Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Тригонометрические и обратные тригонометрические функции


Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института