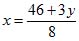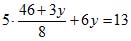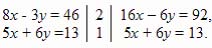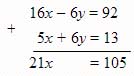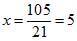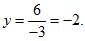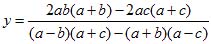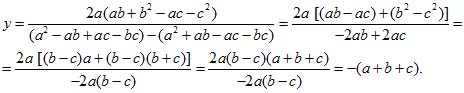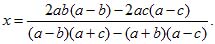а) Способ подстановки состоит в том, что:
1) из одного уравнения мы находим выражение одного из неизвестных, например x, через известные величины и другое неизвестное у,
2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;
3) решаем полученное уравнение и находим значение у; 4) подставляя найденное значение у в выражение неизвестного x, найденное в начале решения, получаем значение х.
Пример. Решить систему уравнений:
8x – 3y = 46, 5x + 6y = 13.
1) Из первого уравнения находим выражение х через данные числа и неизвестное у:
2) Подставляем это выражение во второе уравнение:
3) Решаем полученное уравнение:
5(46+3y)/8 + 48y/8 = 13, 5(46+3y) + 48y = 104, 230 + 15y + 48y = 104, 15y+48y = 104 – 230, 63y = — 126, y = — 2.
4) Найденное значение y = — 2 подставляем в выражение 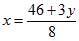
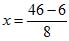
Способ сложения или вычитания
1) обе части одного уравнения умножаются на некоторый множитель; обе части второго уравнения умножаются на другой множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну, и ту же абсолютную величину.
2) Складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки; этим одно из неизвестных исключается.
3) Решаем полученное уравнение с одним неизвестным.
4) Другое неизвестное можно найти тем же приемом, но обычно, проще всего подставить найденное значение первого неизвестного в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.
Пример. Решить систему уравнений:
8x – 3y = 46, 5x + 6y = 13.
1) Проще всего уравнять абсолютные величины коэффициентов при у; обе части первого уравнения умножим на 2; обе части второго — на 1, т. е. оставляем второе уравнение неизменным:
2) Складываем два уравнения:
3) Решаем полученное уравнение:
4) Подставляем значение x = 5 в первое уравнение; имеем: 40 — 3y = 46; — 3y = 46 – 40; — 3y = 6. Отсюда
Способ сложения и вычитания следует предпочесть другим способам:
1) когда в данных уравнениях абсолютные величины коэффициентов при одном из неизвестных равны (тогда первый из этапов решения становится ненужным);
2) когда сразу видно, что числовые коэффициенты при одном из неизвестных уравниваются с помощью небольших целочисленных множителей;
3) когда коэффициенты уравнений содержат буквенные выражения.
Пример. Решить систему:
(a + c)x – (a – с)y = 2ab, (a + b)x – (a — b)y = 2ac.
1) Уравниваем коэффициенты при х, помножая обе части первого уравнения на (a + b), а второго на (а + с), получаем:
(a + c)(a +b)x – (a + b)(a — c)y = 2ab(a + b), (a +c)(a +b)x – (a-b)(a + c)y = 2ac(a +c).
2) Вычитаем из первого уравнения второе; получаем:
[(a — b)(a + c) – (a + b)(a — c)]y = 2ab(a + b) – 2ac(a + c).
3) Решаем полученное уравнение:
Это выражение можно значительно упростить, для чего однако, потребуются довольно долгие преобразования. В числителе и знаменателе раскроем скобки,
4) Чтобы найти x, уравняем коэффициенты при y в исходных уравнениях, помножив первое на (a — b), второе на (a — с). Вычтя одно полученное уравнение из другого, решим уравнение с одним неизвестным; найдем:
Выполняя такие же преобразования, как в предыдущем пункте, получим х = b + c — a. Подстановка значения y d одно из исходных уравнений потребовала бы более утомительных вычислений; при решении буквенных уравнений так бывает очень часто.
Видео:Решение систем уравнений методом подстановкиСкачать

Системы уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
 | x — 4y = 2 |
| 3x — 2y = 16 |
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
Видео:Решение систем уравнений. Методом подстановки. Выразить YСкачать

Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
 | x — 4y = 2 |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3( 2 + 4y ) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
Например, для решение системы:
 | x — 4y = 2 |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
| 2 — x | = | 16 — 3x |
| -4 | -2 |
Решаем уравнение, чтобы узнать значение x:
| ||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Видео:Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
 | x — 4y = 2 |
| 3x — 2y = 16 |
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
 | x — 4y = 2 |
| -6x + 4y = -32 |
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
| + | x — 4y = 2 |
| -6x + 4y = -32 | |
| -5x = -30 |
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
 | 3x — 12y = 6 |
| 3x — 2y = 16 |
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
| — | 3x — 12y = 6 |
| 3x — 2y = 16 | |
| -10y = -10 |
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
| 3x — 2y = 16 |
| 3x — 2 · 1 = 16 |
| 3x — 2 = 16 |
| 3x = 16 + 2 |
| 3x = 18 |
| x = 18 : 3 |
| x = 6 |
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Алгебра. 7 класс
Конспект урока
Решение задач при помощи систем уравнений первой степени
Перечень рассматриваемых вопросов:
• Решение системы уравнений.
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Решить систему – это значит найти все её решения.
Алгебраический способ состоит в получении ответа на вопрос задачи с помощью составления уравнения или системы уравнений и последующего решения уравнения или системы.
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Рассмотрим задачу. Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
Мы не знаем, сколько овец у Ивана, и сколько у Петра.
Обозначим за х число овец у Ивана, а за у – число овец у Петра.
Мысленно разделим условие задачи на две независимые части:
1. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!»
2. А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!»
Для каждой из частей составим уравнение с двумя неизвестными.
Начнем с первой части.
Если бы Пётр отдал Ивану одну овцу, то у Петра осталось бы (у – 1) овец.
А у Ивана стало бы (х + 1) овец.
Но тогда у Ивана было бы вдвое больше овец, чем у Петра.
Можем составить уравнение x + 1 = 2(y – 1).
Составим уравнение с двумя неизвестными для второй части. Если бы Иван отдал Петру 1 овцу, то у Ивана осталось бы (x – 1) овец. А у Петра стало бы (y + 1) овец, и тогда они имели бы овец поровну. Можем составить уравнение: x – 1 = y + 1
Мы составили два уравнения.
И в первом и во втором уравнении х обозначает число овец у Ивана, а у – число овец у Петра. Другими словами, каждое неизвестное число обозначает одно и то же в обоих уравнениях. Значит, эти уравнения можно рассматривать совместно, то есть объединить их в систему уравнений:
Решим эту систему способом подстановки.
Раскроем скобки в правой части первого уравнения.
Выразим х через у.
Подставим (2у – 3) вместо х во второе уравнение системы. Получим уравнение с одним неизвестным у.
Решим его. Упростим левую часть уравнения.
Перенесем неизвестные в левую часть. уравнения, а числа – в правую.
Подставим у = 5 в первое уравнение.
Система имеет единственное решение: х = 7, у = 5.
Вернемся к исходным обозначениям.
Получаем, что у Ивана было 7 овец, а у Петра 5 овец.
Таким образом, мы решили задачу при помощи системы уравнений первой степени.
Задачи с помощью системы уравнений можно решать по следующей схеме.
Сначала вводим обозначения неизвестных.
Мысленно разделив условие задачи на две части, составляем 2 уравнения и объединяем их в систему.
Решаем полученную систему уравнений.
Возвращаемся к условию задачи и использованным обозначениям.
Отбираем решения и записываем ответ.
Разбор заданий из тренировочного модуля.
1. Решим задачу алгебраическим способом.
Даны 3 числа, сумма которых равна 23. Если к удвоенному первому числу прибавить второе число и вычесть третье, то получится 32. А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.
В задаче 3 неизвестные, поэтому введем следующие обозначения:
Пусть х – первое число, у – второе число, z – третье число.
Мысленно разделим условие задачи на 3 части, по каждой из которых составим уравнение с тремя неизвестными:
Вернёмся к условию задачи: первое число 15, второе число 5, третье число 3.
Составим систему уравнений по условию задачи.
В трех сосудах 54л воды. Если из первого перелить во второй сосуд 4л, то в обоих сосудах будет воды поровну, а если из третьего сосуда перелить во второй 17л, то во втором сосуде окажется в 4 раза больше воды, чем в третьем. Сколько воды в каждом сосуде?
Пусть x л воды было в первом сосуде, y л воды – во втором, z воды – в третьем. Значит, всего в трёх сосудах было x + y + z л воды, что равно 54 л. Составим уравнение: x + y + z = 54.
Когда из первого сосуда перелили 4 л воды во второй сосуд, то во втором сосуде стало y + 4 л воды, а в первом сосуде x – 4 л воды. По условию задачи воды стало в сосудах поровну. Составляем уравнение:
Если из третьего сосуда перелить во второй 17 л, то в третьем останется z – 17 л, а во втором станет y + 17 л. По условию задачи во втором сосуде окажется в 4 раза больше воды, чем в третьем. Можем составить уравнение: y + 17 = 4(z – 17).
Записываем систему уравнений:
2. Система уравнений по условию задачи.
Составим систему уравнений по условию задачи: 5% одного числа и 4% другого вместе составляют 46, а 4% первого числа и 5% второго вместе составляют 44. Найдите эти числа.
📽️ Видео
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Начинаем решать 11-й вариант сборника Добротина (номера 1-28)Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение систем уравнений методом сложенияСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Алгебра 7 класс (Урок№46 - Системы двух уравнений первой степени с двумя неизвестными.)Скачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Алгебра.7 класс (Урок№42 - Уравнения первой степени с одним неизвестным.)Скачать

Алгебра 7 класс (Урок№49 - Решение задач при помощи систем уравнений первой степени.)Скачать