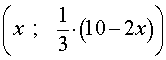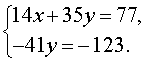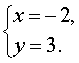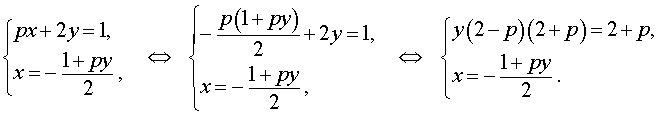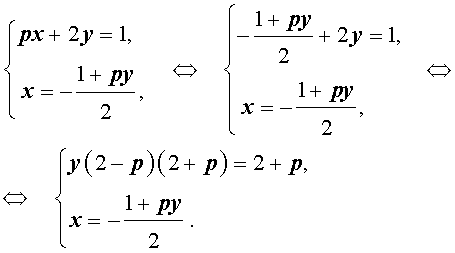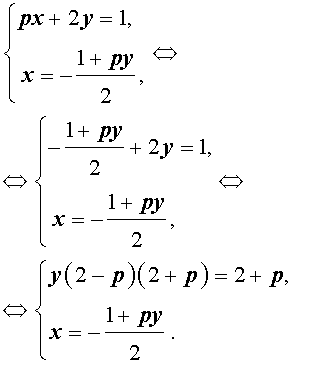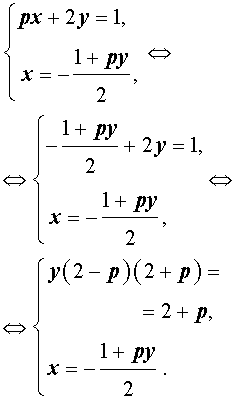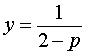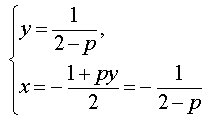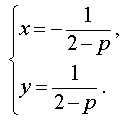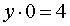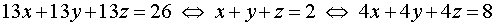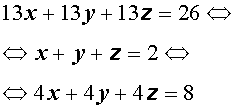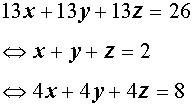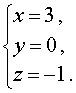Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Линейные уравнения
- Линейные уравнения
- Квадратные уравнения
- Разложение квадратного трехчлена на множители
- Дробно рациональные уравнения
- Системы уравнений
- Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.
- Системы линейных уравнений
- Линейные уравнения (уравнения первой степени) с двумя неизвестными
- Системы из двух линейных уравнений с двумя неизвестными
- Системы из трех линейных уравнений с тремя неизвестными
- Системы линейных уравнений с тремя переменными
- 🎥 Видео
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Линейные уравнения
Линейное уравнение – уравнение вида a x = b , где x – переменная, a и b некоторые числа, причем a ≠ 0 .
Примеры линейных уравнений:
- 3 x = 2
- 2 7 x = − 5
Линейными уравнениями называют не только уравнения вида a x = b , но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.
Как же решать уравнения, которые приведены к виду a x = b ? Достаточно поделить левую и правую часть уравнения на величину a . В результате получим ответ: x = b a .
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Для того, чтобы решить линейное уравнение , необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида a x = b . Решение данного линейного уравнения: x = b a .
Примеры решения линейных уравнений:
- 2 x + 1 = 2 ( x − 3 ) + 8
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
2 x + 1 = 4 x − 6 + 8
В левую часть переносятся все слагаемые с x , в правую – числа:
Теперь поделим левую и правую часть на число ( -2 ) :
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
x 2 + 3 x − 8 = x − 1
Это уравнение не является линейным уравнением.
Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)
- 2 x − 4 = 2 ( x − 2 )
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 2 x = − 4 + 4
И как же здесь искать x , если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом. Запишем ответ к данном линейному уравнению.
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
2 x − 4 = 2 x − 16
2 x − 2 x = − 16 + 4
В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x , при которых равенство становилось бы верным. Запишем ответ к данному линейному уравнению.
Видео:Система с тремя переменнымиСкачать

Квадратные уравнения
Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .
Алгоритм решения квадратного уравнения:
- Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
- Выписать, чему равны в числах коэффициенты: a = … b = … c = …
- Вычислить дискриминант по формуле: D = b 2 − 4 a c
- Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
- Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
- Если D 0, решений нет: x ∈ ∅
Примеры решения квадратного уравнения:
- − x 2 + 6 x + 7 = 0
a = − 1, b = 6, c = 7
D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64
D > 0 – будет два различных корня:
x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7
Ответ: x 1 = − 1, x 2 = 7
a = − 1, b = 4, c = − 4
D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0
D = 0 – будет один корень:
x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2
a = 2, b = − 7, c = 10
D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31
D 0 – решений нет.
Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!
Видео:Как решать уравнения с дробью? #shortsСкачать

Разложение квадратного трехчлена на множители
Квадратный трехчлен можно разложить на множители следующим образом:
a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )
где a – число, коэффициент перед старшим коэффициентом,
x – переменная (то есть буква),
x 1 и x 2 – числа, корни квадратного уравнения a x 2 + b x + c = 0 , которые найдены через дискриминант.
Если квадратное уравнение имеет только один корень , то разложение выглядит так:
a x 2 + b x + c = a ⋅ ( x − x 0 ) 2
Примеры разложения квадратного трехчлена на множители:
- − x 2 + 6 x + 7 = 0 ⇒ x 1 = − 1, x 2 = 7
− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )
- − x 2 + 4 x − 4 = 0 ; ⇒ x 0 = 2
− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2
Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:
- c = 0 ⇒ a x 2 + b x = x ( a x + b )
- b = 0 ⇒ применить формулу сокращенного умножения для разности квадратов.
Видео:Система уравнений. Метод алгебраического сложенияСкачать

Дробно рациональные уравнения
Пусть f ( x ) и g ( x ) – некоторые функции, зависящие от переменной x .
Дробно рациональное уравнение – это уравнение вида f ( x ) g ( x ) = 0 .
Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.
ОДЗ – область допустимых значений переменной.
В выражении вида f ( x ) g ( x ) = 0
ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).
Алгоритм решения дробно рационального уравнения:
- Привести выражение к виду f ( x ) g ( x ) = 0 .
- Выписать ОДЗ: g ( x ) ≠ 0.
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни.
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Пример решения дробного рационального уравнения:
Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.
Решение:
Будем действовать в соответствии с алгоритмом.
- Привести выражение к виду f ( x ) g ( x ) = 0 .
Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:
x 2 − 4 2 − x − 1 2 − x = 0
x 2 − 4 2 − x − 2 − x 2 − x = 0
x 2 − 4 − ( 2 − x ) 2 − x = 0
x 2 − 4 − 2 + x 2 − x = 0
x 2 + x − 6 2 − x = 0
Первый шаг алгоритма выполнен успешно.
Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2
- Приравнять числитель дроби к нулю f ( x ) = 0 и найти корни:
x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.
a = 1, b = 1, c = − 6
D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25
D > 0 – будет два различных корня.
x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3
- Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.
Корни, полученные на предыдущем шаге:
Значит, в ответ идет только один корень, x = − 3.
Видео:Решение систем уравнений методом подстановкиСкачать

Системы уравнений
Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y ) , которые объединены в общую систему фигурной скобкой.
Пример системы уравнений
Решить систему уравнений – найти пару чисел x и y , которые при подстановке в систему уравнений образуют верное равенство в обоих уравнениях системы.
Существует два метода решений систем линейных уравнений:
- Метод подстановки.
- Метод сложения.
Алгоритм решения системы уравнений методом подстановки:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
- Найти оставшуюся неизвестную.
Решить систему уравнений методом подстановки
Решение:
- Выразить из любого уравнения одну переменную через другую.
- Подставить в другое уравнение вместо выраженной переменной полученное значение.
- Решить уравнение с одной неизвестной.
3 ( 8 − 2 y ) − y = − 4
y = − 28 − 7 = 28 7 = 4
- Найти оставшуюся неизвестную.
x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0
Ответ можно записать одним из трех способов:
Решение системы уравнений методом сложения.
Метод сложения основывается на следующем свойстве:
Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.
Решить систему уравнений методом сложения
Давайте избавимся в данном примере от переменной x . Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3 . Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент ( − 3 ) . Для этого домножим левую и правую часть первого уравнения на ( − 3 ) .
Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.
( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )
− 3 x − 6 y + 3 x − y = − 24 − 4
y = − 28 − 7 = 28 7 = 4
Осталось найти переменную x . Для этого подставим y = 4 в любое из двух уравнений системы. Например, в первое.
Ответ можно записать одним из трех способов:
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.
Видео:Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Системы линейных уравнений
 Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
Видео:Решение системы трех уравнений по формулам КрамераСкачать

Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
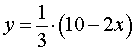 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Видео:Матричный метод решения систем уравненийСкачать

Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
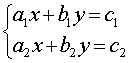 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
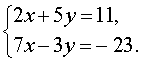 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
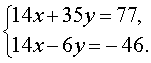 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
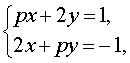 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
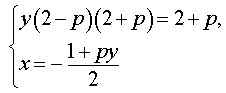 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
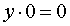
и его решением является любое число 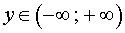
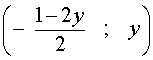
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
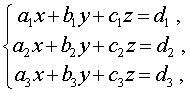 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
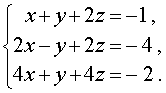 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
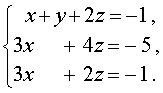 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
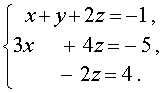 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
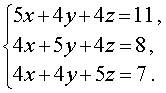 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Системы линейных уравнений с тремя переменными


Линейным уравнением называется уравнение вида:
В этом уравнении — неизвестные, а — действительные (или комплексные) числа. При этом называются коэффициентами уравнения, а — свободным членом.
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
Из трех способов решения этих систем: графического, способа подстановки и способа сложения остается два последних способа. Графический способ уже не проходит, так как пришлось бы находить точку пересечения трех плоскостей. А это трудно изобразить.
Способ подстановки для трех уравнений похож на способ подстановки для двух уравнений с двумя неизвестными, только у этого способа на один шаг больше. Первое: выражаем одно из неизвестных из одного уравнения через два остальных неизвестных и подставляем это выражение в оставшиеся два уравнения. Эти оставшиеся два уравнения составляют систему из двух уравнений с двумя неизвестными. А дальше решаем эту полученную систему и находим два неизвестных, а затем, зная их, и третье неизвестное.
Пример 1 Решить систему уравнений: способом подстановки.
Выразим из первого уравнения через остальные неизвестные и свободный член. Найденное выражение подставим в остальные уравнения.
Далее, оставляя первое уравнение в покое, решаем систему из двух получившихся уравнений с неизвестными и (предварительно разделив обе части второго уравнения на ).
Получили единственное решение системы
Рассмотрим теперь способ сложения. Так же как и для двух уравнений с двумя неизвестными, нужно при помощи сложения уравнений добиться, чтобы одно из неизвестных пропало.Приведем пример.
Пример 2 Решить систему уравнений: способом сложения.
Постараемся получить два уравнения с двумя неизвестными. Избавимся от неизвестной . Для этого удвоенное первое уравнение сложим почленно с удвоенным вторым уравнением, а удвоенное второе уравнение прибавим к третьему уравнению:
Далее производим почленное сложение двух уравнений с двумя неизвестными, исключая неизвестную :
Из последнего уравнения системы находим 
В заключении решим задачу, которая приводится к системе с тремя неизвестными.
Задача В трех урнах — шариков. В первой урне шариков больше чем во второй на столько, сколько шариков в третьей урне. Число шариков во второй урне относится к числу шариков в третьей урне как . Сколько шариков в каждой урне?
Обозначим число шариков в 1-й, 2-й и 3-й урнах через соответственно. Тогда первое условие задачи дает уравнение , второе условие — , а третье условие — . Запишем три полученные уравнения в систему, сделав предварительно третье уравнение линейным:
Складывая почленно первые два уравнения находим .Решаем систему из двух оставшихся уравнений:
Итак, в урнах соответственно и шариков.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.


Нужна помощь с курсовой или дипломной работой?
🎥 Видео
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

МЕТОД ПОДСТАНОВКИ 7 класс СИСТЕМА УРАВНЕНИЙСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решить уравнение с дробями - Математика - 6 классСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать