Как решать рекуррентные неоднородные уравнения

В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.

Видео:Решение неоднородного рекуррентного уравненияСкачать

Как решать рекуррентные соотношения?

Для решения рекуррентных соотношений применяют один из двух основных способов:

• Метод производящих функций
• Метод характеристического уравнения

В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.

Метод производящих функций

1. Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$) $$a_ = …, \ a_ = …, \ a_ = …, \ … \ a_ = …, ngeqslant k$$
2. Домножить каждую строчку на $z$ в соответствующей степени $z^ cdot a_$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_^ a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
3. Решить полученное уравнение относительно $G(z)$.
4. Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.

Метод характеристических функций

Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:

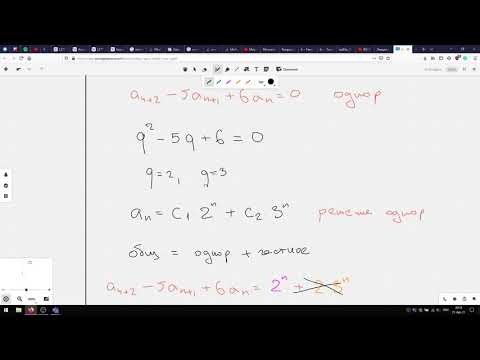
1. Записать соответствующее однородное рекуррентное уравнение (РУ): $$ p_ a_ + p_a_ + . + p_n a_n =f to \ to p_ a_ + p_a_ + . + p_n a_n =0. $$
2. Выписать для него характеристическое уравнение и найти его корни $lambda_i$ $$ p_ lambda^ + p_lambda^ + . + p_lambda + p_n =0. $$
3. Выписать согласно полученным корням $lambda_1, . lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже). $$ C_1 lambda_1^n +. +C_k lambda_k^n , mbox , $$ $$ C_1 lambda_1^n + C_2 nlambda_1^n +. +C_m n^m lambda_1^n+. +C_k lambda_k^n mbox , lambda_1 , , m. $$
4. Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
5. Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
6. Подставить начальные условия $a_0, a_1, . a_$ и получить значения констант $C_1, . C_k$.

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решение для последовательности чисел Фибоначчи

Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:

$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , . $$

Числа Фибоначчи растут быстро: $f_=55$, $f_=6765$, а $f_=354224848179261915075$.

Общая формула данной рекуррентной последовательности имеет вид6

Способ 1. Производящяя функция

Начинаем с второго шага алгоритма, домножаем на $z^n$:

$$begin 1cdot f_0 &= &0cdot 1,\ zcdot f_1 &= &1cdot z,\ zcdot f_n & = &(f_+f_)cdot z^n, quad ngeq2.\ end $$

Складываем все строчки:

На третьем шаге алгоритма приводим все суммы к замкнутому виду:

откуда выводим искомое выражение для производящей функции:

Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:

Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:

Аналогично (но с делением на $z_2$) действуем со второй дробью:

Преобразуем данное выражение, используя то, что

$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt $$ $$f_n=frac<sqrt>left( biggl( frac<1+sqrt> biggr)^n — biggl( frac<1-sqrt> biggr)^n right). $$

Способ 2. Характеристическое уравнение

Запишем характеристический многочлен для $f_n=f_+f_$, и найдем его корни:

Тогда общее решение однородного рекуррентного уравнения имеет вид:

Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.

Решая систему, найдем

Итоговое выражение для последовательности чисел Фибоначчи:

Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.

Видео:21.04 - дискра, рекуррентные соотношенияСкачать

Примеры решений

Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку

Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку

Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$ с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.

Задача 4. Найти последовательность $$, удовлетворяющую рекуррентному соотношению $a_ + 4 a_ + 3 a_ = 0$ и начальным условиям $a_1=2$, $a_2=4$.

Видео:R-1 Рекуррентные соотношения: введениеСкачать

Мудров В.В. Высшая математика в задачах и упражнениях: основы комбинаторного анализа — файл n5.doc

приобрести
Мудров В.В. Высшая математика в задачах и упражнениях: основы комбинаторного анализа
скачать (456.8 kb.)
Доступные файлы (10):

Видео:Неоднородная система линейных уравненийСкачать

n5.doc

Глава 4. Рекуррентные уравнения (соотношения)
4.1. Основные понятия и определения
Рекуррентные уравнения (соотношения), которые ранее уже неоднократно встречались (в том числе получались, строились), являются дискретными аналогами обыкновенных дифференциальных уравнений. Они, в отличие от дифференциальных, используемых в качестве математических моделей непрерывных систем, описывают динамику дискретных (импульсных) систем (одна из таких простейших систем фигурирует, в частности, в задаче Фибоначчи, рассмотренной в главе 2).

Любое рекуррентное уравнение связывает неизвестную величину f (n) – значение бесконечной числовой последовательности (решетчатой функции), служащей решением уравнения, с аналогичными величинами f ( i ), имеющими меньший индекс i ( i 0), характеризующий глубину (продолжительность) связей между элементами искомой последовательности;

g (n) – заданная, как правило, аналитическим выражением последовательность – возмущающая функция натурального аргумента (ее присутствие в рекуррентном уравнении необязательно).

Так, например, три соотношения
f (n+1) = f (n) + 2 sin n ,

f (n+3) = f (n) + 3 f (n+1) ∙ f (n+2)
являются соответственно рекуррентными уравнениями 1-го, 2-го и 3-го порядков. При этом в первых двух уравнениях роль возмущающей функции g (n) выполняют две последовательности
< 2 sin n >, < -5n ∙ exp (- n) >,
а в третьем уравнении функция g (n) отсутствует, т.е. g (n) = 0.

Частное решение (или просто решение) рекуррентного уравнения — любая последовательность (решетчатая функция), удовлетворяющая уравнению (4.1), т.е. приводящая после ее подстановки в рекуррентное уравнение к тождеству.

Так, например, последовательность y (n) = < 2,4,8. , . > является одним из частных решений рекуррентного уравнения
f (n+2) = 10 f (n) – 3 f (n+1),
в чем легко убедиться, если подставить y (n) в это уравнение.

Начальные условия рекуррентного уравнения. Если в (4.1) n = 0, то будем иметь соотношение для k-го элемента последовательности
f (k ) = F [ g (0), f (k-1), f (k-2). f (0) ],
значение которого может быть вычислено с помощью уравнения, если предварительно задать совокупность значений
= . ( 4.2 )

Эти значения (по аналогии с теорией дифференциальных уравнений, когда интегрирование сводится к решению задачи Коши) называются начальными условиями рекуррентного уравнения (4.1).

Общее решение рекуррентного уравнения — последовательность
f (n) = f (n ,C ), ( 4.3 )
зависящая от k произвольных постоянных ( j = 1,2. k ) и отвечающая двум требованиям (см. пример 4.1):

1) для любых допустимых значений произвольных постоянных эта последовательность удовлетворяет уравнению (4.1), т.е. является одним из его частных решений;

2) для любой заданной совокупности начальных условий (4.2) найдутся такие постоянные , что последовательность (4.3) будет удовлетворять этим условиям, т.е. системе k уравнений
, ( i = 0,1,2. k—1)
относительно k искомых значений постоянных .
4.2. Линейные рекуррентные уравнения

с постоянными коэффициентами
Линейное уравнение — рекуррентное соотношение вида
,( 4.4 )
где ( i = 1,2. k ) — коэффициенты уравнения, являющиеся в общем случае функциями натурального аргумента.

Линейное уравнение с постоянными коэффициентами – частный случай уравнения (4.4), когда все коэффициенты — постоянные действительные числа, не зависящие от натурального аргумента n.

Линейное однородное уравнение — линейное рекуррентное уравнение

, ( 4.5 )
у которого отсутствует правая часть, т.е. g (n) = 0.

Свойство аддитивности решений однородного уравнения: если последовательности x (n), y (n) являются частными решениями уравнения (4.5), т.е.

,
то при любых (произвольных ) числах A , B последовательность
z (n) = A ∙ x (n) + B ∙ y (n),
представляющая собой линейную комбинацию решений x (n), y (n), также будет являться решением, т.е. для z (n) будет выполняться
.
Так, например, две последовательности , являются (в чем несложно удостовериться путем подстановки) решениями рекуррентного уравнения
f (n+2) – f (n+1) — 6f (n) = 0. ( 4.6 )
Как следует из свойства аддитивности, решениями уравнения (4.6) будут также любые линейные комбинации этих последовательностей и, в частности, функции натурального аргумента
, ,
где r – любое действительное число. В этом легко убедиться, если z (n) и w (n) подставить в уравнение ( 4.6 ).

Общее решение однородного уравнения — последовательность , представляющая собой линейную комбинацию вида
, ( 4.7 )
где f j (n) ( j = 1,2. k ) — линейно независимые частные решения, составляющие фундаментальную систему решений.

Общее решение неоднородного уравнения — последовательность f (n), которую можно записать в виде суммы
, ( 4.8 )
слагаемыми которой служат

— общее решение однородного уравнения;

— любое частное решение неоднородного уравнения.

Так, для рассмотренного в качестве примера линейного однородного рекуррентного уравнения (4.6) общее решение можно записать в виде линейной комбинации
.
Если это уравнение дополнить правой частью – решетчатой функцией , в результате чего уравнение станет неоднородным, то последовательность

будет удовлетворять полученному неоднородному уравнению
,
т.е. являться его частным решением.

Таким образом, согласно (4.8) общее решение уравнения (4.6) можно записать следующим образом
.
4.3. Построение общего решения

однородного рекуррентного уравнения

по корням характеристического многочлена
Характеристический многочлен линейного рекуррентного уравнения (4.4) с постоянными коэффициентами – полином k—й степени
, ( 4.9 )
получающийся посредством замены на всех f (n + j ) ( j = 0,1. k ), фигурирующих в левой части неоднородного уравнения .

Уравнение принято называть характеристическим уравнением.

Формулировка задачи. Пусть имеется линейное однородное рекуррентное уравнение вида (4.5), в котором все коэффициенты ( i = 1,2. k ) — постоянные действительные числа. Требуется найти его общее решение , т.е. построить фундаментальную систему решений
,
входящих в линейную комбинацию (4.7).

Обоснование возможности использования характеристического многочлена для решения сформулированной задачи.

Запишем решение уравнения в виде и подставим его в (4.5). После преобразований получим
, ( 4.10 )
где есть не что иное, как записанный в виде (4.9) характеристический многочлен.

Так как нас не интересует тривиальное решение ( когда h = 0 ), то из (4.10) следует — аргумент h должен удовлетворять характеристическому уравнению . Решая это уравнение, получим (с учетом кратности) k корней. Каждому корню соответствует одно частное решение, причем аналитический вид решения зависит от типа (характера) корня (действительный, комплексный, кратный).

Правила определения вида частных решений уравнения (4.5) по корням характеристического многочлена:

1. Если h — простой (однократный) действительный корень, то ему соответствует частное решение вида
. ( 4.11 )
2. Если h = a + ib — простой комплексный корень, то этому корню и сопряженному с ним (т.е. паре сопряженных корней) соответствуют два линейно независимых частных решения

( 4.12 )

— модуль комплексного числа (комплексного корня) ;

? = arctg ( b / a ) — аргумент комплексного числа .
3. Если h — действительный корень кратности m, то ему

(точнее всем совпадающим корням ) соответствуют частные решения
, , . , ( 4.13 )
составляющие группу m линейно независимых функций натурального аргумента.
4. Если h = a + ib — комплексный корень кратности m, то с учетом предыдущих правил группе совпадающих пар сопряженных корней соответствуют частные решения
( 4.14 )

составляющие группу 2m линейно независимых функций натурального аргумента.

Порядок построения общего решения линейного однородного рекуррентного уравнения с постоянными коэффициентами:

1. По заданному рекуррентному уравнению (4.5) записываем характеристический многочлен (4.9) и находим его корни.

2. Каждому корню характеристического уравнения, строго придерживаясь сформулированных правил и выражений (4.11)– (4.14), ставим в соответствие одно частное решение.

3. Используя полученную на предыдущем этапе совокупность частных решений (фундаментальную систему решений), записываем искомое общее решение в виде линейной комбинации (4.7).

Построению общих решений конкретных линейных однородных рекуррентных уравнений с помощью сформулированных выше правил посвящен пример 4.2.

1. Нахождение частного решения

неоднородного рекуррентного уравнения

с помощью метода неопределенных коэффициентов
Метод неопределенных коэффициентов предназначен (как и в случае интегрирования дифференциальных уравнений) для нахождения частного решения линейного неоднородного рекуррентного уравнения (4.4) с постоянными коэффициентами. Он применим в ситуации, когда правая часть g ( n ) уравнения представляет собой некоторую сумму, слагаемыми которой служат функции натурального аргумента двух видов:
, ( 4.15 )

, ( 4.16 )
в которых b,  — действительные числа, а d(n), , — полиномы относительно переменной n с действительными коэффициентами.

Ниже рассматривается возможность применения метода неопределенных коэффициентов, когда правая часть g (n) рекуррентного уравнения является последовательностью вида (4.15). Для правой части вида (4.16) удобнее использовать рассматриваемый в следующей главе операционный подход.

Формулировка задачи. Пусть имеется линейное неоднородное рекуррентное уравнение с постоянными коэффициентами
( 4.17 )
в котором d (n) — полином s-й степени,
.
Требуется с помощью метода неопределенных коэффициентов найти аналитическое выражение частного решения записанного уравнения.

Правила определения аналитического вида частного решения неоднородного уравнения (4.17):

1. Если b не принадлежит к корням характеристического многочлена (4.9), то частное решение будет иметь вид

, ( 4.18 )
где D (n) – полином с неизвестными (неопределенными) коэффициентами,

, ( 4.19 )
порядок которого совпадает с порядком заданного полинома d ( n ).

2. Если b — действительный корень характеристического многочлена (4.9) кратности m, то частное решение будет иметь вид
( 4.20 )
где D (n) – полином вида (4.19).

Порядок нахождения частного решения линейного неоднородного рекуррентного уравнения с постоянными коэффициентами:

1. По заданному рекуррентному уравнению (4.17) записываем характеристический многочлен (4.9).

2. Проверяем, является ли величина b корнем характеристического уравнения, и если да, то определяем его кратность m.

3. Записываем, строго придерживаясь сформулированных правил и выражений (4.18) –(4.20), аналитический вид частного решения .

4. Подставив частное решение в рекуррентное уравнение, после преобразований получаем — слева и справа от знака равенства стоят многочлены s-й степени.

5. Приравнивая коэффициенты при одинаковых степенях натурального аргумента n, получим систему (s+1) уравнений относительно неизвестных коэффициентов

6. Решая систему линейных алгебраических уравнений, определяем коэффициенты полинома (4.19) и записываем конкретный вид искомого частного решения.

Замечание. Если корни характеристического уравнения известны, то выполнение пункта 2 не вызывает трудностей. В противном случае можно предложить следующий алгоритм (не требующий вычисления корней). Сначала проверяем (посредством подстановки в характеристическое уравнение ), является ли величина b корнем. Если да, то путем последовательного дифференцирования характеристического многочлена и подстановки величины b в его производные находим порядок первой, не обращающейся в ноль, производной. Именно этот порядок и будет искомой кратностью m корня.

Нахождению с помощью сформулированных выше правил частных решений линейных неоднородных рекуррентных уравнений с различными правыми частями посвящен пример 4.3.

1. Определение решения рекуррентного уравнения, удовлетворяющего заданным начальным условиям

Формулировка задачи. Пусть имеется линейное неоднородное рекуррентное уравнение и известно его общее решение
( 4.21 )
в котором — любое частное решение, а (j = 1,2. k) – решения, образующие фундаментальную систему решений однородного уравнения .

Требуется среди всего множества решений, составляющих общее решение (4.21), выделить (найти) единственное решение , удовлетворяющее заданным начальным условиям f (i) ( i = 0,1. k-1).

Система уравнений для нахождения решения — линейная неоднородная алгебраическая система k уравнений относительно совокупности неизвестных постоянных

квадратная матрица которой составлена из значений = элементов последовательностей ( j = 1,2. k ), входящих в фундаментальную систему решений.

Замечание 1. Система всегда совместна и имеет единственное решение, так как ее квадратная матрица является (в силу независимости фундаментальной системы решений) невырожденной, т.е. определитель матрицы не равен нулю.

Замечание 2. Ясно, что в ситуации, когда исходное рекуррентное уравнение однородное, частное решение = 0 и, как следствие, все значения , входящие в правую часть системы, будут нулевыми.

Порядок нахождения решения линейного неоднородного рекуррентного уравнения по заданным начальным условиям:

1. Вычисляем значения последовательностей , для всех

значений n = i (i = 0,1. k-1) и записываем систему (4.22).

2. Решая алгебраическую систему, находим неизвестные постоянные (j = 1,2. k).

3. Подставляя в общее решение (4.21) вместо найденные значения постоянных , получаем конечный аналитический вид искомого решения f (n,).

В примере 4.4 для двух линейных рекуррентных уравнений (однородного и неоднородного) с заданными начальными условиями находятся решения, удовлетворяющие этим условиям. При этом в качестве однородного фигурирует уравнение, описывающее динамику изменения последовательности чисел Фибоначчи.

Примеры задач с решениями
Пример 4.1. Показать, что общее решение рекуррентного уравнения
f (n+2) = 7∙f (n+1) — 12∙f (n)
можно записать в виде

.
Легко проверить, что последовательность f (n) при любых значениях произвольных констант обращает заданное рекуррентное уравнение в тождество, т.е. первое требование к общему решению удовлетворяется. Действительно,

Чтобы убедиться в выполнении второго требования, выберем в качестве начальных условий произвольные числа A, B, т.е. f (0 ) = A,

f (1) = B. Так как из предполагаемого общего решения имеем
, ,
то для нахождения постоянных используем систему линейных уравнений

Решая эту систему, получим аналитические выражения для искомых величин

.
Из полученных выражений следует — для любых начальных условий A, B существует единственная последовательность
,
удовлетворяющая этим условиям и самому рекуррентному уравнению, что подтверждает выполнение второго требования к общему решению.
Пример 4.2. Найти общие решения однородных рекуррентных уравнений
a) f (n+3) – 9 f (n+2) + 26 f (n+1) – 24 f (n) = 0,

б) f (n+4) – f (n) = 0,

1. в) f (n+3) + 6 f (n+2) + 12 f (n+1) + 8 f (n) = 0,

г) f (n+4) + 2 f (n+2) + f (n) = 0.
a) Характеристическое уравнение, соответствующее первому из заданных рекуррентных уравненений,
,
имеет три различных действительных корня
.
В соответствии с правилом 1 функции натурального аргумента

составляют фундаментальную систему решений. В итоге общее решение рекуррентного уравнения имеет вид

.
б) Характеристическое уравнение

имеет четыре различных корня:

два комплексных сопряженных ;

два действительных .

В соответствии с правилами 1, 2 четыре линейно независимые функции натурального аргумента

в которых  = , составляют фундаментальную систему решений.

Следовательно, искомое общее решение рекуррентного уравнения имеет вид
.
в) Характеристическое уравнение

имеет один корень h = — 2 кратности m = 3.

Согласно правилу 3, фундаментальную систему решений составляют три функции натурального аргумента

и, как следствие, искомое общее решение рекуррентного уравнения записывается в виде равенства
.
г) Характеристическое уравнение

имеет два комплексных сопряженных корня кратности m = 2. В этом случае, согласно правилу 4, фундаментальная система решений включает четыре линейно независимые функции натурального аргумента

в которых  =  , и общее решение однородного рекуррентного уравнения имеет вид
.

Пример 4.3. Найти частное решение рекуррентного уравнения

для следующих вариантов правых частей:
a) а = 5, d (n) = 12,

в) а = 3, d (n) = 2.
Запишем характеристический многочлен
,
который является общим для всех вариантов исходных данных и имеет три различных действительных корня
.
а) Число а = 5 не относится к корням характеристического многочлена (R (5) = 6). Учитывая, что полином d (n) = 12 в правой части имеет нулевой порядок, записываем (в соответствии с правилом 1) аналитический вид частного решения и подставляем его в исходное уравнение. В результате будем иметь равенство
,
из которого находим D = 2, т.е. искомое частное решение можно записать в виде
.
б) Число а = — 2 также не относится к корням характеристического многочлена ( R (-2) = — 120 ). В данном случае полином d (n) имеет первый порядок, т.е. согласно правилу 1, неизвестный полином D (n), входящий в частное решение, можно записать следующим образом
D (n) = An + B,
где A, B — неопределенные коэффициенты. Подставим частное решение в рекуррентное уравнение

и преобразуем полученное выражение с учетом равенств
D ( n + 1 ) = A∙n + ( A + B ),

в результате чего будем иметь
.
Приравнивая коэффициенты при одинаковых степенях n (при нулевой и первой), получим систему уравнений

-148 А – 120В = 28,
разрешая которую, находим A = -1, B = 1, т.е. искомое частное решение можно записать следующим образом
.
в) Число а = 3 является простым (однократным) корнем характеристического многочлена. Для данного варианта исходный полином d (n) = 2 .

Записываем, согласно правилу 2, аналитический вид частного решения и подставляем его в исходное уравнение
.
После сокращения на и приведения подобных членов несложно заметить, что будет выполняться равенство
,
где R (3), — значения характеристического многочлена и его производной при h = 3.

Учитывая R (3) = 0, получаем , т.е. D существует, если значение отлично от нуля. Это подтверждает необходимость строгого соблюдения правила 2 (проверки и учета кратности корня).

Так как в рассматриваемом случае , то и искомое решение имеет вид

.
Пример 4.4. Найти решения рекуррентных уравнений с известными начальными условиями:
a) f (n+2) – f (n+1) – f (n) = 0, f (0) = 1, f (1) = 2,
б) f (n+2) – 2 f (n+1) + f (n) = 6n, f (0) = 1, f (1) = 3.
a) Характеристическое уравнение

имеет два действительных корня
, ( А = ).
Следовательно, фундаментальную систему решений составляют две функции натурального аргумента
, ,
а общее решение имеет вид
.
Вычисляем необходимые значения функций ( n = 0,1 ):
, , ,
и записываем систему линейных уравнений относительно неизвестных значений произвольных постоянных:

Решая эту систему, получим выражения для неизвестных величин
, .
После подстановки последних в общее решение записываем аналитический вид искомого решения, удовлетворяющего заданным начальным условиям:
.
На первый взгляд, кажется удивительным, что это выражение, с помощью которого получаются числа Фибоначчи, для любого n принимает целые значения.

б) Характеристическое уравнение

имеет один действительный корень h = 1 кратности m = 2. Следовательно, фундаментальную систему решений составляют две функции

а общее решение однородного уравнения записывается следующим образом

.
Правая часть рекуррентного уравнения, согласно условиям примера, имеет вид (4.15) с параметрами
a = 1, d ( n ) = 6 n,

т.е. a = h = 1 — двукратный корень характеристического уравнения.

Исходя из этого, записываем аналитический вид частного решения

и подставляем его в исходное уравнение
.
После преобразования имеем 6A∙n + 6A + 2B = 6n. Приравнивая коэффициенты при одинаковых степенях n, получаем систему уравнений
6 A = 6,

6 A + 2 B = 0,
разрешая которую, находим A = 1, B = — 3, т.е. частное решение неоднородного уравнения удовлетворяет равенству
,
а с учетом ранее записанного его общее решение имеет вид
.
Для нахождения решения, удовлетворяющего начальным условиям, вычисляем значения функций , , ( n = 0,1 )
=1, =1, =0, =1, , ,
записываем систему линейных уравнений

и, решая эту систему, получаем .

Подставляя полученные значения в общее решение, будем иметь функцию натурального аргумента
f (n) = (n – 3)∙+ 4 n + 1,
представляющую искомое частное решение, удовлетворяющее заданным начальным условиям.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дискретная математика — рекуррентное соотношение

В этой главе мы обсудим, как рекурсивные методы могут выводить последовательности и использоваться для решения задач подсчета. Процедура поиска членов последовательности рекурсивным способом называется рекуррентным отношением . Мы изучаем теорию линейных рекуррентных соотношений и их решения. Наконец, мы вводим производящие функции для решения рекуррентных отношений.

Видео:9. Решение рекуррентных соотношений. Дискретная математика.Скачать

Определение

Рекуррентное отношение — это уравнение, которое рекурсивно определяет последовательность, в которой следующий член является функцией предыдущих членов (выражая F n как некоторую комбинацию F i с i n ).

Пример — ряд Фибоначчи — F n = F n − 1 + F n − 2 , Ханойская башня — F n = 2 F n − 1 + 1

Видео:Решение рекуррентных уравненийСкачать

Линейные рекуррентные отношения

Линейное рекуррентное уравнение степени k или порядка k — это рекуррентное уравнение в формате x n = A 1 x n − 1 + A 2 x n − 1 + A 3 x n − 1 + d o t s A k x n k ( A n — константа, а A k n e q 0 ) на последовательности чисел как полинома первой степени.

Вот некоторые примеры линейных рекуррентных уравнений —

Как решить линейное рекуррентное соотношение

Предположим, что два упорядоченных линейных рекуррентных соотношения имеют вид — F n = A F n − 1 + B F n − 2 , где A и B — действительные числа.

Характеристическое уравнение для вышеуказанного рекуррентного соотношения —

x 2 − A x e − B = 0

Три случая могут возникнуть при поиске корней —

Случай 1 — Если это уравнение учитывается как ( x − x 1 ) ( x − x 1 ) = 0 и оно дает два различных реальных корня x 1 и x 2 , то F n = a x n 1 + b x n 2 является решение. [Здесь a и b являются константами]

Случай 2 — Если это уравнение вычисляется как ( x − x 1 ) 2 = 0 , и оно порождает один действительный корень x 1 , то решением является F n = a x n 1 + b n x n 1 .

Случай 3 — Если уравнение дает два различных комплексных корня, x 1 и x 2 в полярной форме x 1 = r a n g l e t h e t a и x 2 = r a n g l e ( − t h e t a ) , то F n = r n ( a c o s ( n t h e t a ) + b s i n ( n t h e t a ) ) является решением.

Решите рекуррентное соотношение F n = 5 F n − 1 − 6 F n − 2 , где F 0 = 1 и F 1 = 4 .

Характеристическое уравнение рекуррентного соотношения —

Итак, ( x − 3 ) ( x − 2 ) = 0

x 1 = 3 и x 2 = 2

Корни реальны и различны. Итак, это в форме дела 1

F n = a x n 1 + b x n 2

Здесь F n = a 3 n + b 2 n ( A s x 1 = 3 a n d x 2 = 2 )

1 = F 0 = a 3 0 + b 2 0 = a + b

4 = F 1 = a 3 1 + b 2 1 = 3 a + 2 b

Решая эти два уравнения, мы получаем a = 2 и b = − 1

Следовательно, окончательное решение —

$$ F_n = 2,3 ^ n + (-1). 2 ^ n = 2,3 ^ n — 2 ^ n $$

Решите рекуррентное соотношение — F n = 10 F n − 1 − 25 F n − 2 , где F 0 = 3 и F 1 = 17 .

Характеристическое уравнение рекуррентного соотношения —

x 2 − 10 x − 25 = 0

Итак, ( x − 5 ) 2 = 0

Следовательно, существует один действительный корень x 1 = 5

Поскольку существует единый действительный корень, он имеет вид случая 2

F n = a x n 1 + b n x n 1

3 = F 0 = a .5 0 + b .0 .5 0 = a

17 = F 1 = a .5 1 + b .1 .5 1 = 5 a + 5 b

Решая эти два уравнения, мы получаем a = 3 и b = 2 / 5

Следовательно, окончательное решение — F n = 3.5 n + ( 2 / 5 ) . n .2 n

Решите рекуррентное соотношение F n = 2 F n − 1 − 2 F n − 2 , где F 0 = 1 и F 1 = 3

Характеристическое уравнение рекуррентного соотношения —

📹 Видео

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейные рекуррентные соотношения || Гущин Д. Д.Скачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Рекуррентные уравненияСкачать

Рекуррентное вычисление определителя порядка nСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Райгородский А. М. - Комбинаторика - Линейные рекуррентные соотношенияСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Рекуррентное уравнениеСкачать

18. Линейные неоднородные дифференциальные уравнения 2 порядка с постоянными коэффициентами. часть 3Скачать

10. Линейные однородные рекуррентные соотношения. Дискретная математикаСкачать

R-16 Случай неоднородных соотношенийСкачать