Как решать неполные квадратные уравнения подробно (8 видео)

Неполные квадратные уравнения

Неполное квадратное уравнение – это уравнение вида

в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид:

ax 2 + bx = 0,	если c = 0;
ax 2 + c = 0,	если b = 0;
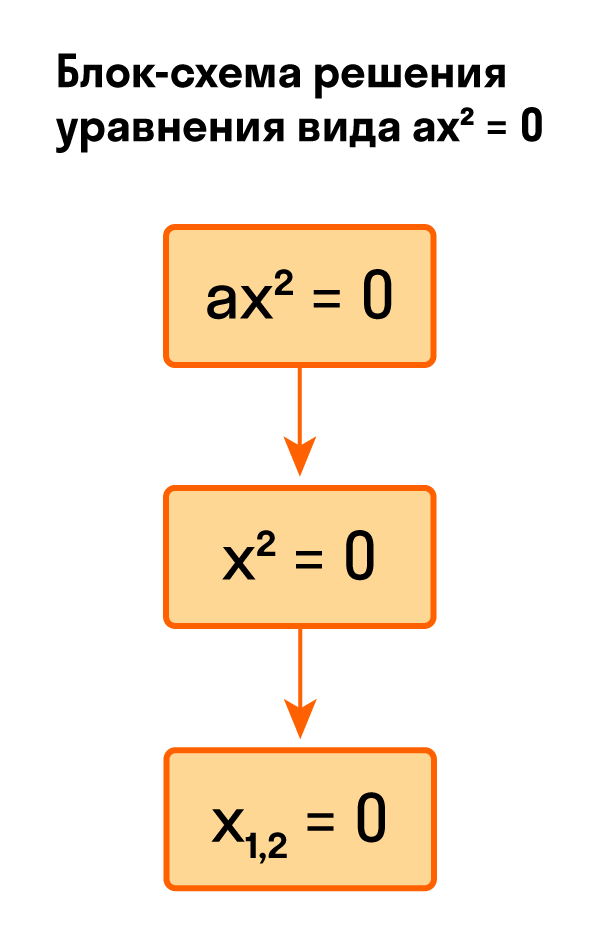
ax 2 = 0,	если b = 0 и c = 0.

Содержание

Решение неполных квадратных уравнений
Методы решения неполных квадратных уравнений
Алгоритм нахождения решений
Уравнение вида ax2+bx=0 при отсутствии c
ax2+c=0 при b равном нулю
Особый вид уравнения
Другие способы решения неполных уравнений
Видео
Неполные квадратные уравнения
Основные понятия
Решение неполных квадратных уравнений
Как решить уравнение ax² = 0
Как решить уравнение ax² + с = 0
В двух словах
Как решить уравнение ax² + bx = 0
Видео

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение неполных квадратных уравнений

Чтобы решить уравнение вида ax 2 + bx = 0 , надо разложить левую часть уравнения на множители, вынеся x за скобки:

Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит:

Чтобы ax + b было равно нулю, нужно, чтобы

x = —	b	.
	a

Следовательно, уравнение ax 2 + bx = 0 имеет два корня:

x₁ = 0 и x₂ = —	b	.
	a

Неполные квадратные уравнения вида ax 2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю.

Пример 1. Решите уравнение:

a 2 — 12a = 0
a(a — 12) = 0
a₁ = 0	a — 12 = 0
a₂ = 12

Пример 2. Решите уравнение:

7x 2 = x
7x 2 — x = 0
x(7x — 1) = 0

x₁ = 0

7x — 1 = 0

7x = 1

x₂ =	1
	7

Чтобы решить уравнение вида ax 2 + c = 0 , надо перенести свободный член уравнения c в правую часть:

ax 2 = —c, следовательно, x 2 = —	c	.
	a

В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа.

Если данное неполное уравнение будет иметь вид x 2 — c = 0 , то сначала опять переносим свободный член в правую часть и получаем:

В этом случае уравнение будет иметь два противоположных корня:

Неполное квадратное уравнение вида ax 2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами.

Пример 1. Решите уравнение:

24 = 2y 2
24 — 2y 2 = 0
-2y 2 = -24
y 2 = 12
y₁ = +√ 12	y₂ = -√ 12

Пример 2. Решите уравнение:

b 2 — 16 = 0
b 2 = 16
b₁ = 4	b₂ = -4

Уравнение вида ax 2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax 2 = 0 следует, что x 2 = 0, значит, и x = 0. Любое другое значение x не будет являться корнем данного уравнения.

Видео:НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ 8 классСкачать

Методы решения неполных квадратных уравнений

Научившись решать уравнения первой степени, хочется научиться работать с более сложными уравнениями, например, с квадратными. Многим известно, как решаются стандартные квадратные уравнения, но есть особый вид таких выражений, которые называют квадратные уравнения в краткой записи. Рассмотрим подробнее, как решать неполные квадратные уравнения.

Видео:МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать

Алгоритм нахождения решений

На сегодняшний день существует три вида таких выражений. В зависимости от этого каждое решение имеет свои особенности, от которых зависит решение конкретного примера, будь оно целым или в виде иррационального числа.

Уравнение вида ax2+bx=0 при отсутствии c

Это наиболее распространенное выражение в укороченном типе с квадратными корнями. Как решить нечто похожее в этом случае? Для этого надо разложить левую часть на множители. Алгоритм решения следующий, и обычно не меняется:

Раскладываем выражение как x*(ax+b), равное нулю.
Так как выражение равно нулю, если хотя бы один из множителей равен ему, то запишем следующую систему уравнений в виде x и ax+b=0.
Первое решение так и пишется x=0. Второе равенство линейное и решается как равное -b/a.

В качестве примера приведем следующее равенство: x2+18x=0. Раскладываем его в виде x*(x+18)=0. Получаем x=0 и -18. Оба решения являются правильными и подойдут под результат. Также решаются и остальные выражения, относящиеся к неполным квадратным уравнениям такого вида.

ax2+c=0 при b равном нулю

Не такой частый, но встречающийся тип квадратного выражения. Здесь имеются два корня, отличающиеся лишь знаками, в крайнем случае корней не имеется вообще.

План действий для решения такого выражения разберем на следующем примере:

Имеем уравнение x2−49=0 или аналогичное ему.
Раскладываем его как (x-7)*(x+7)=0.
Получаем решение типа x=7 и -7.
Записываем ответ в виде двух корней.

А вот при одинаковых знаках в записи решения не будет в принципе. Например, для выражения 25×2+1=0 не имеется ответа, потому что сумма положительных чисел никогда не может равняться нулю.

В школьном курсе алгебры эти равенства стараются решить так, чтобы прийти к формату x2=d. То есть 9×2−2 равно нулю. Тогда x2=2/9, а ответом послужат два одинаковых корня с разными знаками.

Особый вид уравнения

Имеется также один особый тип укороченного выражения. Он имеет следующий вид ax2, которое равно нулю. У таких уравнений имеется решение в виде единственного корня. В учебниках есть указание, что решение состоит в виде двух корней, каждый из которых равен нулю.

Видео:АЛГЕБРА 8 класс : Решение неполных квадратных уравнений | ВидеоурокСкачать

Другие способы решения неполных уравнений

Любое подобное выражение в квадрате можно решить, не применяя формулу квадратных корней. К таким видам решения называют формулу сокращенного умножения и правило деления на число.

Допустим, выражение 5×2=0. В этом выражении только умножение на ноль даст результат, а значит, единственный ответ здесь x=0.

Теперь возьмем выражение вида 5×2=125. Делим обе части уравнения на 5. Получим следующий промежуточный результат: x2=25. Переносим все в левую часть и получится x2−25=0. Затем используем формулу разности квадратов в виде (x-5)*(x+5)=0. Получаем итоговый результат в виде x=5 или x=-5.

Далее разберем, как решить вышеописанными способами равенство 16*x2-x=0. Выносится общий множитель за скобки x*(16x-1)=0. Получается два варианта ответа: x=0 и 16x=1. После этого делим каждую часть на 16, в итоге получаем x=1/16. Записываем итоговый ответ в виде x1=0 и x2=1/16.

Стоит отметить, что если вы не знаете, как применить формулы сокращенного умножения или деления на число, то лучше применить способ решения такого выражения согласно стандартным правилам решения квадратного уравнения. Каким именно методом решить данные квадратные выражения, выбирает сам человек. Иногда самые очевидные способы решения не подойдут для определенного примера, может и вовсе не оказаться конкретных ответов. Также не является обязательным такой вариант, как стандартные целые числа.

Здесь могут быть и иррациональные числа, а также дробные. Все будет зависеть от конкретного выражения.

Не являющиеся полными примеры по типу квадрата, несмотря на свое название, решаются достаточно просто. Можно применить как стандартные методы нахождения ответа, например, квадратные корни, так и формулы сокращенного умножения, а также деления на число.

При этом нельзя сказать, что какой-либо из вышеописанных способов является универсальным. Под каждое конкретное уравнение подбирается свой способ нахождения ответа. Не забывайте также о том, что не все такие квадратные равенства имеют ответ, иногда у них нет корней вовсе. Это верно, если оба числа являются положительными, а их сумма не может равняться нулю.

Видео:РЕШЕНИЕ НЕПОЛНОГО КВАДРАТНОГО УРАВНЕНИЯ ЗА 5 СЕКУНДСкачать

Видео

Из видео вы узнаете способы решения неполных квадратных уравнений.

Видео:Как решать неполное квадратное уравнение? 😎Скачать

Неполные квадратные уравнения

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Алгебра 8 класс (Урок№27 - Квадратные уравнения. Неполные квадратные уравнения.)Скачать

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Решение неполных квадратных уравнений

Как мы уже знаем, есть три формулы неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!

Видео:Как решать неполные квадратные уравненияСкачать

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при — c/а 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Разделим обе части на 9:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Разделим обе части на -1:

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Видео:Как решать неполные квадратные уравнения.Скачать

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 2x² — 32x = 0

Это уравнение равносильно х = 0 и 2x — 32 = 0.

Решить линейное уравнение:

Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² — 12x = 0

Разложить левую часть уравнения на множители и найти корни: