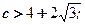План урока:
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Модуль числа
Напомним, что такое модуль числа. Так называют значение числа, взятое без учета его знака. То есть модуль чисел 9 и (– 9) одинаков и равен 9. Для обозначения модуля применяют специальные прямоугольные скобки:
|2,536| = |– 2,536| = 2,536
Грубо говоря, операция нахождения модуля сводится к отбрасыванию у числа знака «минус», если он у него есть. Вообще, если число х неотрицательно, то его модуль |х| = х. Если же число отрицательно, то его модуль имеет противоположное значение: |х| = х. Математически это можно записать так:
Именно такое определение обычно и применяется в математике.
Модуль играет важную роль в математике. Дело в том, с его помощью удобно записывать расстояние между двумя точками на координатной прямой. Пусть на ней отмечены точки a и b. Расстояние между ними равно |a – b|, причем неважно, какое из этих чисел больше, а какое меньше:
Также модуль возникает при извлечении квадратного корня из четной степени числа:
В частности, если n = 1, получим формулу:
Для того чтобы получить график функции у = |x|, сначала надо построить график функции без учета знака модуля:
Далее следует выполнить преобразование. Те точки графика, которые располагаются выше оси Ох, остаются на своем месте. В данном случае это та часть графика, которая находится в I четверти. Те же точки, которые располагаются ниже оси Ох, должны быть симметрично (относительно этой самой оси Ох) отображены. В результате они окажутся выше оси Ох:
В результате получилась «галочка».
Пример. Постройте график ф-ции у = |х 2 – 4х + 3|
Решение. Для построения графика функции, содержащей модуль, сначала надо построить график для «подмодульного» выражения. Поэтому построим график у = х 2 – 4х + 3. Это квадратичная ф-ция, ее график – это парабола:
Часть графика, в промежутке от 1 до 3, находится ниже оси Ох. Чтобы построить ф-цию у = |х 2 – 4х + 3|, надо перевернуть эту часть графика:
Видео:Как решать уравнение с параметром и модулем ★ Решите уравнение: x-|x|=aСкачать

Решение уравнений с модулем
Изучим простейший случай уравнения, содержащего модуль, когда вся его слева записано выр-ние в модульных скобках, а справа находится число. То есть уравнение имеет вид
где b – какое-то число, а у(х) – произвольная ф-ция.
Если b 10 + 97x 4 – 12,56х 3 + 52х 2 + 1001х – 1234| = – 15
Решение: Справа стоит отрицательное число. Однако модуль не может быть меньше нуля. Это значит, что у ур-ния отсутствуют корни.
Ответ: корни отсутствуют.
Если b = 0, то мы получим какое-то произвольное ур-ние у(х) = 0, у которого могут быть корни. Проще говоря, модульные скобки в таком случае можно просто убрать.
Пример. Решите ур-ние
Ясно, что подмодульное выр-ние равно нулю:
Наиболее интересен случай, когда b> 0, то есть в правой части стоит положительное число. Ясно, что тогда под модулем находится либо само это число b, либо противоположное ему число – b:
То есть мы получаем два различных ур-ния: у(х) = bи у(х) = – b.
Пример. Решите ур-ние
Решение. В правой части – положительное число, поэтому либо х = – 10, либо х = 10.
Пример. Решите ур-ние
Решение. Исходное ур-ние разбивается на два других ур-ния:
10х + 5 = 7 или 10х + 5 = – 7
10х = 2 или 10х = – 12
х = 0,2 или х = – 1,2
Пример. Найдите корни ур-ния
Решение. Снова заменим исходное равенство на два других:
x 2 – 2х – 4 = 4 или x 2 – 2х – 4 = – 4
Имеем два квадратных ур-ния. Решим каждое из них:
D = b 2 – 4ас = (– 2) 2 – 4•1•(– 8) = 4 + 32 = 36
Нашли корни (– 2) и 4. Решаем второе ур-ние:
х = 0 или х – 2 = 0
Получили ещё два корня: 0 и 2.
Встречаются случаи, когда в уравнении, содержащем знак модуля, под ним находятся обе части равенства:
Здесь возможны два варианта. Либо подмодульные выр-ния равны друг другу (у(х) = g(x)), либо у них противоположные значения (у(х) = – g(x)). То есть снова надо решить два ур-ния.
Пример. Решите ур-ние
|x 2 + 2x– 1| = |х + 1|
Решение. Выр-ния справа и слева (без знака модуля) либо равны, либо противоположны. Можно составить два ур-ния:
x 2 + 2x– 1 = х + 1 или x 2 + 2x– 1 = – (х + 1)
х 2 + х – 2 = 0 или х 2 + 3х = 0
Решим 1-ое ур-ние:
D = b 2 – 4ас = 1 2 – 4•1•(– 2) = 1 + 8 = 9
Теперь переходим ко 2-омуур-нию:
х = 0 или х + 3 = 0
Всего удалось найти 4 корня: (– 1), (– 2), 2 и 0.
Возможен случай, когда в левой части равенства находится модуль выр-ния, а в правой – обычное выражение, без модуля. Такое ур-ние имеет вид |у(х)| = g(x). Здесь также возможны два варианта: у(х) = g(x) или у(х) = – g(x). Однако следует учитывать ещё один факт. Модуль не может быть отрицательным, а потому должно выполняться нер-во g(x)⩾ 0. Но это неравенство не надо решать. Достаточно просто подставить в него все полученные корни и проверить, справедливо ли нер-во.
Пример. Найдите решение уравнения, содержащего модуль:
|х 2 + 3,5х – 20| = 4,5х
Решение. Рассмотрим два отдельных равенства:
х 2 + 3,5х – 20 = 4,5х илих 2 + 3,5х – 20 = – 4,5х
х 2 – х – 20 = 0 или х 2 + 8х – 20 = 0
Решим каждое из полученных квадратных ур-ний.
D = b 2 – 4ас = 1 2 – 4•1•(– 20) = 1 + 80 = 81
D = b 2 – 4ас = 8 2 – 4•1•(– 20) = 64 + 80 = 144
Итак, получили 4 корня: (– 4), 5, (– 10) и 2. Однако правая часть исходного ур-ния, 4,5x, не может быть отрицательной, ведь модуль числа – это всегда неотрицательная величина:
Для х = – 4 и х = – 10 это условие не выполняется, поэтому эти корни должны быть исключены.
Мы рассмотрели три случая, когда ур-ние имеет вид:
Однако порою ур-ние не удается свести ни к одному из этих видов. Тогда для решения уравнений и неравенств, содержащих модуль, следует рассматривать их на отдельных интервалах, где подмодульные выр-ния не изменяют свой знак.
Пример. Найдите корни ур-ния
Решение. Выр-ния х + 1 и х – 4 меняют знак при переходе через точки (– 1) и 4:
Если отметить обе точки на прямой, то они образуют на ней 3 интервала:
Исследуем ур-ние на каждом из полученных промежутков.
Так как при х 2 + bx + c = 0
Параметры встречаются не только при описании ур-ний, но и, например, при рассмотрении функций. Так, линейная функция задается формулой у = kx + b. Здесь числа k и b являются параметрами. Так как ур-ние у = kx + b задает на плоскости прямую линию, то величины k и b порою называют параметрами уравнения прямой.
Если при решении обычного ур-ния мы определяем значение его корней в виде конкретных чисел, то при решении ур-ний с параметром находят формулу, позволяющую при заданном значении параметра вычислить значение корня.
Пример. Решите ур-ние
и найдите его корни при значении параметра а, равном 3.
Решение. Вынесем множитель х за скобки:
х = 0 или х – 2а = 0
Получили, что при любом значении параметра а ур-ние имеет два корня. Один из них равен нулю при любом значении а, а второй вычисляется по формуле х = 2а:
при а = 3х = 2•3 = 6
Ответ: есть два корня – 0 и 2а. При а = 2 корни равны 0 и 6.
Пример. Решите ур-ние
р 2 х – 3рх = р 2 – 9
Решение. Слева вынесем за скобки множитель рх, а выр-ние справа преобразуем, используя формулу разности квадратов:
рх(р – 3) = (р – 3)(р + 3)
Возникает желание поделить обе части рав-ва на р(р – 3), чтобы выразить х. Однако сразу так делать нельзя, ведь если величина р(р – 3) равна нулю, то получится деление на ноль.
Поэтому сначала изучим случаи, когда один из множителей слева равен нулю. Если р = 0, то мы получим рав-во
0•х•(0 – 3) = (0 – 3) (3 – 0)
Это неверное тождество, а потому при р = 0 ур-ние корней не имеет.
Если р – 3 = 0, то есть р = 3, получится следующее
Это равенство верно при любом х. Значит, при р = 3 корнем ур-ния является любое число.
Если же р≠ 0 и р ≠ 3, то произведение р(р – 3) также не равно нулю, а потому обе части равенства можно поделить на р(р – 3). Тогда получим
В этом случае ур-ние имеет единственный корень.
Ответ: при р = 0 корней нет; при р = 3 корнем является любое число; при других рх = (р + 3)/р.
Часто в задаче требуется не выразить корень ур-ния через параметр, а лишь оценить количество корней ур-ния или диапазон их значений.
Пример. Сколько корней имеет ур-ние
при различных значениях параметра b.
Решение. Будем решать ур-ние графическим методом. Для этого сначала построим график у = |х 2 – 6х + 5|. В модульных скобках находится обычная квадратичная функция, чьи ветви смотрят вверх. Найдем нули функции:
D = b 2 – 4ас = (– 6) 2 – 4•1•5 = 36 + 20 = 16
Итак, нули ф-ции – это точки 1 и 5. Найдем координату х0 вершины параболы по формуле:
Подставив х0 в квадратичную ф-цию найдем координату у0 вершины параболы:
3 2 – 6•3 + 5 = 9 – 18 + 5 = – 4
Теперь построим квадратичную ф-цию:
Для построения графика, содержащего модуль функции, надо отобразить точки с отрицательными ординатами (они находятся ниже оси Ох) симметрично относительно оси Ох:
Мы построили график левой части ур-ния. График правой части представляет собой горизонтальную прямую у = b. Можно выделить 5 различных случаев взаимного расположения этих графиков:
При b 4 есть горизонтальная прямая пересекает график лишь в 2 точках, то есть получаем 2 корня.
Ответ: нет корней при b 4; 3 корня при b = 4; 4 корня при 0 4 – (а + 2)х 2 + 3а – 3 = 0
имеет ровно 4 корня?
Решение. Это ур-ние является биквадратным, то есть для его решения нужно произвести замену у = х 2 :
у 2 – (а + 2)у + 3а – 3 = 0 (1)
Для того, чтобы исходное ур-ние имело 4 корня, необходимо, чтобы у квадратного уравнения с параметром(1) было два положительных корня: у1 и у2. Тогда, проводя обратную замену х 2 = у1 и х 2 = у2, мы получим два разных квадратных ур-ния, корни которых будут равны
Если же хоть один из двух корней, например, у1, окажется равным нулю, то величины
Совпадут (они обе будут равны нулю), и останется лишь 3 корня. Если же у1 будет отрицательным числом, то ур-ние
вовсе не будет иметь решений, и тогда останется не более 2 корней.
Итак, решим ур-ние (1):
у 2 – (а + 2)у + 3а – 3 = 0
D = b 2 – 4ас = (– (а + 2)) 2 – 4•1•(3а – 3) = (а + 2) 2 – 12 а + 12 =
= а 2 + 4а + 4 – 12а + 12 = а 2 – 8а + 16 = а 2 – 2•4•а + 4 2 = (а – 4) 2
Чтобы у ур-ния (1) было два различных корня, дискриминант должен быть положительным. Величина (а – 4) 2 положительна при всех значениях а, кроме а = 4, которое обращает дискриминант в ноль. Значит, а ≠ 4.
Извлечем корень из дискриминанта:
Корни ур-ния (1) можно вычислить по формулам:
И у1, и у2 должны быть положительными величинами, однако у1 меньше, чем у2 (ведь для его вычисления дискриминант брали со знаком «минус», а не «плюс»). Поэтому достаточно записать нер-во:
Получили неравенство, содержащее модуль. Для избавления от модульных скобок в нер-ве рассмотрим 2 случая. Если а – 4>0, то есть а > 4, выполняется равенство
Это нер-во выполняется при любом допустимом значении а, поэтому при а >4 исходное ур-ние имеет 4 корня.
Итак, при условии, что а 1. Это значит, что а∊(1; 4). С учетом первого случая, при котором было получено решение
можно записать окончательный ответ: а∊(1; 4)∪(4; + ∞).
Пример. При каких параметрах а у ур-ния
х 2 – 2(а + 1)х + а 2 + 2а – 3 = 0
существует два корня, которые принадлежат интервалу (– 5; 5)?
Решение. Данное ур-ние является квадратным. Найдем его дискриминант:
D = b 2 – 4ас = (– 2(а + 1)) 2 – 4•1•( а 2 + 2а – 3) = 4(а 2 + 2а + 1) – 4(а 2 + 2а – 3) =
= 4(а 2 + 2а + 1 – а 2 – 2а + 3) = 4•4 = 16
Получаем, что при любом а дискриминант положителен, а потому уур-ния 2 корня. Вычислить их можно по формулам
Для того, чтобы оба решения уравнения с параметром принадлежали интервалу (– 5; 5), нужно, чтобы меньший из них (это х1) был больше – 5, больший (это х2) – меньше – 5:
Значит, должны выполняться два нер-ва
х1>– 5и х2 – 5 и а + 3 – 4 и а 1 (-1)
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Решение уравнений с модулями и параметрами
Презентация к уроку
Загрузить презентацию (434 кБ)
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные: научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие: развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные: воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a, если a > 0, число – a, если a <
Неравенство | x | 0) равносильно двойному неравенству – a 0.
Неравенство | x | > a, (если a > 0) равносильно двум неравенствам
Неравенство | x | > a, (если a : | x + 3 | + | y – 2 | = 4;
Расcмотрим четыре случая
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 < | x + 3 < | x 0 | y > – 2 |
| – x – 3 – y – 2 = 4 | y = x + 9 |
| < | x + 3 < | x 2 – 1) х = а + 1. Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи: 1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения 2) а = – 1; получаем ОX = О , и очевидно х – любое. Ответ: 3. Решения примеров (из вариантов С) 1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня. Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 | Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой
Числовая прямая при этом разбивает на 5 промежутков
Для случая 3) х0 = – b | 2a = 2, y0 = 25 : 2 + 25 – 10 = 2,5 Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10. Построим график функции, заданной равенством Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 2 – | x | = 6 1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10 1. Решить уравнение | x – 5 | – | 2x + 3| = 10 5. Итог урока 1. Определение модуля. 6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012 Видео:Сможешь решить уравнение с параметром? Что делать с модулем и при чем тут гипербола?Скачать  Уравнения с параметром, содержащие модуль По свойству модуля при всех уравнение будет иметь уравнение будет иметь единственное решение на промежутке x ≥ 5. на промежутке x 1 уравнение имеет два корня При a 1, Раскроем модуль на двух промежутках: уравнение имеет два корня при a + 9 ≥ 0, т.е. a ≥ – 9 неравенство имеет решение Т.е. при a > 0 a ≥ 0; т.е. 0 ≤ a ≤ 9; Т.е. при 0 ≤ a ≤ 9 уравнение имеет два различных корня. уравнение имеет два равных корня Ответим на поставленный вопрос. 2) y = – a – линейная функция, график прямая, параллельная оси OY.
Эскиз графиков. y
Найдем нули модуля: 2x + 6 = 0; x = –3; Раскроем модуль на двух промежутках: x ≥ –3 и x 3 /4 |
|
|
При 

Ответ: 


При каких значениях a уравнение 

 |
При каких значениях параметра a уравнение 
Так как 


Для того чтобы исходное уравнение имело два различных корня, новое уравнение должно иметь только один положительный корень. Это будет в двух следующих случаях:
а) один из корней положителен, другой отрицателен. Для этого достаточно, чтобы дискриминант был положительным, а произведение корней было отрицательным;
б) оба равных корня положительны. Для этого достаточно, чтобы дискриминант был равен нулю, а сумма корней была положительной.
Таким образом, получим совокупность двух систем.


Так как
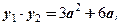






Откуда 
Ответ: 
При каких значениях с уравнение x 2 – ( 3c – 2 ) ∙ | x | + 2c 2 – c = 0 имеет 4 различных корня?
Для того чтобы исходное уравнение могло иметь четыре различных корня новое уравнение должно иметь два положительных корня. Это будет в том случае, когда дискриминант, произведение и сумма корней будут положительны.
Таким образом, получим систему неравенств:



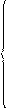
3c – 2 > 0; 
2c 2 – c > 0;
Ответ:
1. М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич. Сборник задач по алгебре 8-9.Москва, 2000
2. Г.А. Ястребинецкий. Задачи с параметрами. Москва, 1986
3. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992
4. В.В.Ткачук. Математика-абитуриенту,т1.Москва, 1994
5. С.Л.Попцов. Как решать задачи с параметром. Тверь, 1999
6. Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави, Москва, 2003
📸 Видео
✓ Четыре способа решить параметр с модулем | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

Самая сложная тема из ЕГЭ. Задание с ПАРАМЕТРОМ | Математика TutorOnlineСкачать

Уравнения с параметром. Алгебра, 8 классСкачать

8 класс, 39 урок, Задачи с параметрамиСкачать

Уравнения с модулемСкачать

Алгебра 8 класс (Урок№33 - Уравнения с параметром. Контрольный урок.)Скачать

Уравнения с параметром. Алгебра 7 класс.Скачать

✓ Параметр с модулями | ЕГЭ-2021. Задание 17. Математика. Профильный уровень | Борис ТрушинСкачать

Уравнение с параметром | Математика TutorOnlineСкачать

✓ Параметр с тройным модулем | ЕГЭ. Задание 17. Математика. Профильный уровень | Борис ТрушинСкачать

Профильный ЕГЭ 2023 математика. Задача 17. Параметр. Аналитический методСкачать

✓ Пять способов решить задачу с параметром | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать

9 класс, 7 урок, Задачи с параметрамиСкачать

11 класс, 34 урок, Задачи с параметрамиСкачать

Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

Уравнение с параметром #4 (Хитрый модуль) ЕГЭ №507512Скачать




 Решить в зависимости от значений параметра а.
Решить в зависимости от значений параметра а. левая часть уравнения неотрицательна, следовательно, при a 0 x – 3 = ± a, откуда x = 3 ± a.
левая часть уравнения неотрицательна, следовательно, при a 0 x – 3 = ± a, откуда x = 3 ± a. единственное решение
единственное решение 
 ;
;  ;
; . уравнение имеет два корня
. уравнение имеет два корня
 x ≥ – 3;
x ≥ – 3;  a ≥ – 9
a ≥ – 9 a ≤ 9; уравнение имеет один корень
a ≤ 9; уравнение имеет один корень
 .
.



 y = – a
y = – a