Как решать квадратные уравнения по теореме пифагора

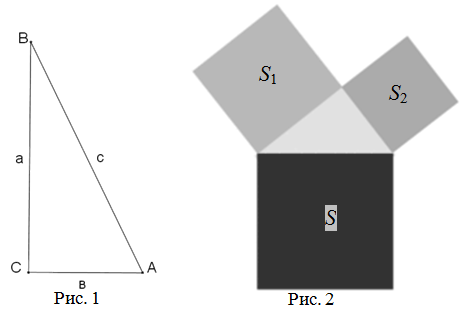
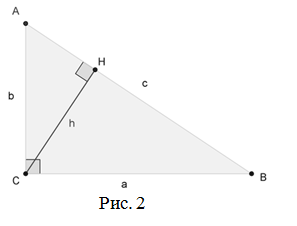
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².

Видео:Теорема Виета за 30 сек🦾Скачать

Доказательство

Доказательство теоремы Пифагора, используя алгебру

Нужно доказать, что c² = a² + b²:

Это квадрат, в котором есть 4 одинаковых треугольника abc:

1. Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
2. Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
3. Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
4. Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
5. Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:

(a + b) (a + b) = c² + 2ab

a² + 2ab + b² = c² + 2ab

Что и требовалось доказать.

«Пифагоровы штаны на все стороны равны»

Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора

На этой фигуре c — гипотенуза, a и b — катеты.

Проведём перпендикулярную линию к гипотенузе (c):

Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).

1. Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
2. Делим «Пифагоровы штаны» на 3 похожие фигуры:

Что и требовалось доказать.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Примеры

Задача 1

На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.

Подставить известные значения

Ответ: длина гипотенузы равна 5.

Задача 2

Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.

Подставить известные значения

Ответ: длина другой стороны треугольника равна 5.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Следствия из теоремы Пифагора

Это основные следствия теоремы:

1. В прямоугольном треугольнике гипотенуза всегда больше любого из двух катетов.
2. Если применить формулу теоремы Пифагора (c² = a² + b²) и равенство будет верным, (т.е. если квадрат одной стороны равен сумме квадратов двух других сторон), то треугольник прямоугольный.
3. Из формулы теоремы Пифагора также можно посчитать любой из катетов: a² = c² − b² либо b² = c² − a².
4. Любой косинус (cos) острого угла будет меньше 1.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Кто придумал теорему Пифагора

Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).

Узнайте также, что такое Теорема Виета и Аксиома.

Видео:Как решить квадратное уравнение (Положительный дискриминант)Скачать

Теорема Пифагора

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

• если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Видео:8 класс, 16 урок, Теорема ПифагораСкачать

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Видео:8 класс, 17 урок, Теорема, обратная теореме ПифагораСкачать

Теорема Пифагора

Видео:Теорема ПИФАГОРА ❤️Скачать

Формула теоремы Пифагора

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов (рис. 1):

Видео:Теорема ПифагораСкачать

Доказательство теоремы Пифагора

Пусть треугольник $A B C$ — прямоугольный треугольник с прямым углом $C$ (рис. 2).

Проведём высоту из вершины $C$ на гипотенузу $A B$, основание высоты обозначим как $H$ .

Прямоугольный треугольник $A C H$ подобен треугольнику $A B C$ по двум углам ( $angle A C B=angle C H A=90^$, $angle A$ — общий). Аналогично, треугольник $C B H$ подобен $A B C$ .

из подобия треугольников получаем, что

Отсюда имеем, что

$$a^=c cdot H B, b^=c cdot A H$$

Сложив полученные равенства, получаем

$$a^+b^=c cdot H B+c cdot A H$$

Что и требовалось доказать.

Видео:ТЕОРЕМА ВИЕТА // Как решать Квадратные Уравнения по АЛГЕБРЕ 8 классСкачать

Геометрическая формулировка теоремы Пифагора

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 2):

Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Примеры решения задач

Задание. Задан прямоугольный треугольник $A B C$, катеты которого равны 6 см и 8 см. Найти гипотенузу этого треугольника.

Решение. Согласно условию катеты $a=6$ см, $b=8$ см. Тогда, согласно теореме Пифагора, квадрат гипотенузы

Отсюда получаем, что искомая гипотенуза

Ответ. 10 см

Задание. Найти площадь прямоугольного треугольника, если известно, что один из его катетов на 5 см больше другого, а гипотенуза равна 25 см.

Решение. Пусть $x$ см — длина меньшего катета, тогда $(x+5)$ см — длина большего. Тогда согласно теореме Пифагора имеем:

Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:

Согласно теореме Виета, получаем, что

Значение $x_$ не удовлетворяет условию задачи, а значит, меньший катет равен 15 см, а больший — 20 см.

Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть

Ответ. $S=150left(mathrm^right)$

Видео:Геометрия 8 класс (Урок№12 - Теорема Пифагора.)Скачать

Историческая справка

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

В древнекитайской книге «Чжоу би суань цзин» говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. Крупнейший немецкий историк математики Мориц Кантор (1829 — 1920) считает, что равенство $3^+4^=5^$ было известно уже египтянам ещё около 2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного прямоугольного треугольника.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Видео:Теорема ВиетаСкачать

Остались вопросы?

Здесь вы найдете ответы.

Согласно теореме Пифагора, значение длины гипотенузы (с) треугольника с прямыми углами, возведенное в квадратную степень, является величиной, равной сумме его катетов (а и b), каждый из которых также возведен в квадрат. Наглядно и с применением условных обозначений это выглядит так:

В теореме Пифагора говорится о том, что в треугольнике с прямыми углами сумма длин катетов, каждая из которых возведена в квадрат, равна длине его гипотенузы, также возведенной в квадратную степень.

При этом под гипотенузой понимается сторона, которая расположена противоположно прямому углу. Катетом считается одна из сторон, участвующих в образовании прямого угла.

Основание прямоугольного треугольника обозначим как Н. Из его вершины С проведем высоту на гипотенузу АВ. Получившийся в результате этого треугольник АСН является подобным треугольнику АВС по двум углам, равным 90º (∠ACB =∠CHA).

В обоих треугольниках есть один общий угол — ∠A.

Подобными также являются треугольные фигуры АВС и СВН. Основанием их подобия являются прямые углы (∠ACB =∠CHB). Оба эти треугольника имеют общий угол, которым является ∠B.

Для продолжения доказательства теоремы Пифагора следует ввести дополнительные обозначения: BC = a, AC = b, AB = c.

На основании полученной ранее информации о подобии треугольников можно утверждать, что:

a/с = HB/a, b/с = AH/b.

Полученное равенство также позволяет сделать следующий вывод:

a2 = c * HB, b2 = c * AH.

На следующем этапе произведем сложение полученных ранее равенств:

a2 + b2 = c * HB + c * AH

Вынесем за скобки общий множитель во второй части равенства:

a2 + b2 = c * (HB + AH)

Теперь можно сократить Н в левой части равенства, в результате получим:

В приведенных выше обозначениях указано, что АВ = с. Это позволяет переписать равенство следующим образом:

a2 + b2 = c * c, или a2 + b2 = c2

Таким образом, теорема Пифагора доказана.

Согласно теореме Пифагора, длина гипотенузы прямоугольного треугольника, которая возведена в квадрат, равна сумме, полученной в результате сложения квадратов длин его катетов. Из этого следует, что:

Извлечем квадрат из обеих частей равенства, в итоге получим:

x = √(5² + 5²)= √(25+25) = √50 = √25*2 = 5√2

Ответ: длина гипотенузы прямоугольного треугольника, катет которого равен 5 см, составляет 5√2, что равно примерно 7,07 см.

Теорема Пифагора не может быть применима к треугольнику с тупыми или острыми углами. Она выполняется только в случае прямоугольного треугольника.

Для треугольника с углом 90º справедливо утверждение о том, что длина его гипотенузы, возведенная во вторую степень, равна сумме длин его катетов, взятых в квадрат.

В теореме Пифагора говорится о том, что сумма длин катетов прямоугольного треугольника, возведенных во вторую степень, равна квадрату длины его гипотенузы. В случае с треугольником, некоторые параметры которого приведены в задании, это утверждение выглядит следующим образом:

х² = 7²-6² = 49-36 = 13.

Для того чтобы найти значение х, нужно извлечь квадратный корень из числа 13:

Ответ: Длина второго катета прямоугольного треугольника равна корню квадратному из 13.

Для решения поставленной задачи следует воспользоваться теоремой Пифагора, которая говорит о том, что сумма длин катетов треугольника с прямым углом, возведенных в квадрат, равна длине его гипотенузы, также возведенной во вторую степень:

Теорема Пифагора может быть применима в данном случае по причине того, что образованная между двумя домами конструкция является прямоугольным треугольником. Зная о том, что сумма квадратов катетов в прямоугольном треугольнике равна длине его катета, возведенной в квадрат, можно вычислить длину неизвестного катета:

24 м – 16 м = 8 м.

Длина одного катета треугольника равна 16 м, второго – 8 м. Зная это, можно применить теорему Пифагора для вычисления длины гипотенузы:

(16*16) + (8*8) = 256 + 64 = 320 м.

Осталось только извлечь квадратный корень из 320, для того чтобы узнать длину расстояния между крышами двух домов.

Ответ: Расстояние между крышами домов равно корню квадратному из 320.

Обозначим длину неизвестного катета как х. Зная то, что по теореме Пифагора длина гипотенузы прямоугольного треугольника, возведенная во вторую степень, равна сумме длин его катетов, которые также возведены в квадрат, можно выразить длину неизвестного катета следующим образом:

х² = 132 – 122 = 169 – 144 = 25

Теперь, для того чтобы узнать длину второго катета, необходимо извлечь квадратный корень из числа 25:

Ответ: длина второго катета прямоугольного треугольника равна 5 см.

Известно, что длина медианы (m), которая проведена к гипотенузе прямоугольного треугольника, равна ½ ее длины. Используя это, можно высчитать длину гипотенузы прямоугольного треугольника:

с = 2*m = 2*6,5 = 13 см.

Высчитав длину гипотенузы и зная длину одного из катетов прямоугольного треугольника, можно вычислить, чему равен его второй катет. Для этого можно использовать теорему Пифагора, согласно которой:

Выражаем из записанного выше равенства длину неизвестного катета:

Из полученного числа нужно извлечь квадратный корень, для того чтобы узнать длину второго катета прямоугольного треугольника:

Ответ: Длина второго катета прямоугольного треугольника равна 12 см.

Равенство, указанное в задании, применимо к треугольнику с прямым углом, как гласит теорема Пифагора.

Каждая из сторон треугольника может быть обозначена прописной буквой, которая соответствует строчной букве, обозначающей угол треугольника, расположенный противоположно этой стороне. На основании этого можно сделать вывод о том, что искомый треугольник является прямоугольным и имеет гипотенузу f и катеты a и b:

Ответ: имеется треугольник АDF с прямым углом F.

Теорема, которая является обратной теореме Пифагора, существует. Согласно этой теореме, треугольник считается прямоугольным в том случае, если длина его большей стороны, возведенная в квадратную степень, равна сумме длин двух других его сторон, которые также возведены в квадратную степень.

Для начала следует провести высоту (h) к основанию равнобедренного треугольника. Данная высота, проведенная к основанию, в случае с равнобедренным треугольником является медианой.

Теперь можно высчитать длину высоты, используя теорему Пифагора. Она будет равна:

h = √((48 см)² — (25,5 см)²) = 10,5√15 см.

Площадь (S) треугольника рассчитывается путем деления на число, полученное в результате умножения длины высоты на длину основания треугольника:

S = ½*10,5√15 см*51 см = 267,75√15 см².

Ответ: Площадь треугольника равна 267,75√15 см².

В равностороннем треугольнике высота (h), проведенная к его основанию, является также его биссектрисой и медианой. Она делит равносторонний треугольник на две части, которые являются равными треугольниками с прямым углом. Их гипотенуза равна а, а катеты – а/2. Для ответа на поставленный вопрос следует применить теорему Пифагора:

Обозначим меньший из катетов как х. Тогда другой катет, длина которого в два раза больше, будет обозначен как 2х. Если в случае с прямоугольным треугольником, длина гипотенузы которого равна √15, применить теорему Пифагора, то она будет выглядеть следующим образом:

После раскрытия скобок в уравнении получаем следующее равенство:

Складываем слагаемые в первой части и получаем:

Сокращаем обе части уравнения на 5, и в итоге получается, что:

Ответ: Длина меньшего из катетов треугольника равна √3, а большего – 2√3.

Если обозначить длину неизвестного катета через х, то гипотенуза будет равна 180-х. Используя введенные обозначения, запишем теорему Пифагора для данного треугольника:

После сокращений получается следующее равенство:

Теперь можно найти значение х:

Длина второго катета равна 80 см.

Зная, что катет в 80 см и неизвестная длина гипотенузы в сумме дают 180 см, можно вычислить длину гипотенузы:

Ответ: Длина гипотенузы равна 100 см.

АВСD является прямоугольной трапецией, у которой AB=9 см и CD=18 см. Диагональ АС данной трапеции составляет 15 см. При этом ВС и AD остаются неизвестными величинами. Длину ВС можно вычислить по следующей формуле:

Произведем перенос высоты:

Тогда получаем, что:

Ответ: Длина основания AD прямоугольной трапеции равна 12+9√3 см.

🎥 Видео

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Теорема Пифагора и решение квадратных уравненийСкачать

ТЕОРЕМА ПИФАГОРА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Теорема Виета. 8 класс.Скачать