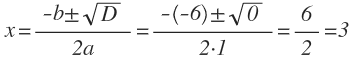Как решать квадратные уравнения через дискриминант с модулем (7 видео)

Решение квадратных уравнений с модулем
учебно-методический материал по алгебре (8 класс)

Урок. Решение квадратных уравнений с модулем

Содержание

Скачать:
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Урок по теме «Квадратные уравнения, содержащие неизвестную под знаком модуля»
Как найти дискриминант квадратного уравнения
Понятие квадратного уравнения
Понятие дискриминанта
Как решать квадратные уравнения через дискриминант
Примеры решения квадратных уравнений с помощью дискриминанта
📸 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Скачать:

Вложение	Размер
урок	26.32 КБ

Видео:#120 Урок 45. Квадратные уравнения с модулем. Алгебра 8 класс. Решить уравнение. Модуль. Математика.Скачать

Предварительный просмотр:

Тема: « Решение квадратных уравнений с

Цель урока: Научить решать квадратные уравнения с модулем с

использованием определения модуля и введением

Организационный момент. (3 мин.)
Повторение изученного материала: (5 мин.)

Способы решения квадратных уравнений:

а) решение квадратных уравнений общим способом (через Д);

б) решение квадратных уравнений с чётным вторым коэффициентом (через Д/4)

в) решение квадратных уравнений с использованием теоремы, обратной теореме Виета;

г) решение квадратных уравнений через сумму коэффициентов

Объяснение нового материала: (20 мин.)

1. Решить уравнение : х 2 – 7IхI + 6 = 0.

а) Используя определение модуля, данное уравнение можно заменить совокупностью двух уравнений:

х 2 – 7х + 6 = 0 и х 2 + 7х + 6 = 0;

х = 1, х = 6; х = -1, х = -6.

Ответ: .

б) Учитывая, что IxI 2 = x 2 , и, обозначив IxI = у, где у 0, данное уравнение можно записать в виде:

х = х = 6

Ответ: .

2. Решить уравнение: (х – 2) 2 – 8I х – 2I + 15 = 0.

Вопрос: Чем данное уравнение отличается от предыдущего?

После ответа на поставленный вопрос, учащиеся решают данное уравнение в тетрадях, сверяя, если есть затруднения, с решением на доске, которое выполняет учащийся.

3. Решить уравнение: х 2 + 4х + Iх +3I + 3 = 0.

Данное уравнение отличается от предыдущих тем, что сумма первых двух слагаемых не является полным квадратом третьего слагаемого. Поэтому, при решении данного уравнения необходимо найти точки, при переходе через которые выражение под знаком модуля изменяет знак. Для этого решаем уравнение

Х + 3 = 0, х = -3. Далее раскрываем знак модуля, используя определение, для х — 3.

При х 2 + 4х — х — 3 + 3 + 0, х 2 + 3х + 0, х = 0, х = -3, но оба эти корни не удовлетворяют условию х

При х — 3, х 2 + 4х + х + 3 + 3 + 0, х 2 + 5х + 6 = 0, х = -2, х = -3.

4. Решить уравнение: х 2 + 17 = 9х + 4Iх – 3I.

Данное уравнение учащиеся решают в тетрадях, сверяя по необходимости с решением, которое выполняет учащийся на доске.

Ответ: ; .

Закрепление изученного материала: (15 мин).

Примеры для самостоятельного решения в классе:

х 2 + 2IхI – 1 = 0, отв. — 1; 1 —
х 2 + 5 IхI -24 = 0, отв. -3; 3.
(2х -3) 2 – 5I2х-3I – 6 = 0. отв. -1,5; 4,5.
2х 2 – 4Iх – 6I +7х = -11, отв. -6,5; 1.
(2х – 1) (IxI – 1) = -0,5. отв. ; .
Ix 2 +2x +3I = 3х +45 отв.-6; 7.

Данные примеры учащиеся выполняют под контролем учителя, при необходимости учащимся оказывается индивидуальная помощь.

Подведение итогов урока. Домашнее задание. (2 мин).

Примеры для домашнего задания:

4х 2 – 3IxI + х = 0,
Ix-2Iх 2 = 10 – 5х,
(х + 4) 2 — 7(х + 4) – 8 = 0,
х 2 – 5х — = 0.
Ix 2 – 4x -9I = 4x.

Тема: «Решение квадратных неравенств с модулем».

Цель урока: Научить решать неравенства второй степени с модулем

по определению модуля и с использованием свойств

Организационный момент. (2 мин.)
Устный опрос и проверка домашнего задания. (10 мин.)

а) Ответить на вопросы учащихся (если есть) и проверить решение примеров:

1. х 2 – 5х — =0,

х = 6, (-1 – не удовлетворяет условию)

оба корня 2 и 3 не удовлетворяют условию.

2. I x 2 – 4x -9I =4х.

По смыслу модуля, данное уравнение решаем для х 0.

x 2 – 4x -9 =4х, x 2 – 4x -9 =-4х

х 2 – 8х -9 = 0, х 2 – 9 = 0,

х = 9, (-1 не удовлетворят х = 3, (-3 не удовлетворяет условию) условию)

б) Решить уравнения (устно):

х 2 – 8IxI + 7 = 0 Отв. -1; -7; 1; 7.

2. х 2 – 10IxI -11 = 0 Отв. -11; 11.

3. х 2 – IxI + 17 = 0 Отв. нет решений.

в) Решить линейные неравенства:

2. IxI > 5; отв. (- ; -5) (5; + )

3. I6x — 42I 0; отв. 7.

4. I7x — 56I решений нет.

III. Объяснение и закрепление нового материала. (30 мин)

Объяснение нового материала построено на разборе трёх типовых неравенств с последующим закреплением при решении подобных примеров.

Решить неравенство: х 2 – 8IxI — 9 .

Обозначив левую часть неравенства через У, и введя новую переменную t = IxI, (t 0), найдём промежуток, на котором функция У = х 2 – 8IxI – 9 принимает значения меньше 0. Это интервал (-1; 9).

Учитывая, что t = IxI, и t 0 при любом х, получим линейное неравенство IxI

Решить неравенство: -4х 2 – 7IxI +11 ≤ 0.

Вопрос: Чем данное неравенство отличается от предыдущего?

После ответа на поставленный вопрос, учащиеся решают данное неравенство в тетрадях, сверяя, если есть затруднения, с решением на доске, которое выполняет учащийся.

Ответ: (- ; -1] [1; + ).

Решить неравенство: х 2 — 7х + 12

Находим точки при переходе через которые выражение под знаком модуля изменяет знак:

Рассмотрим два случая:

б) х 4, тогда х 2 — 7х + 12

Очевидно, что это неравенство решений не имеет.

4. Решить неравенство: х 2 — 13х + 42 Ix – 7I.

Данное неравенство учащиеся решают в тетрадях, сверяя по необходимости с решением, которое выполняет учащийся на доске.

Ответ: (- ; 5] [7; + ).

5 Решить неравенство: Ix 2 – 2xI ≤ -x.

При решении данного неравенства будем пользоваться свойством: IaI ≤ b -b ≤ a ≤ b .

x 2 – 2x ≤ -x,

x 2 – x ≤ 0,

Изобразив решение каждого неравенства на числовой прямой, получим:

◦////////////////////◦ x \\\\\\\\ ///////// x

х = 0 – единственное решение данного неравенства.

Решить неравенство: Ix 2 – 3x – 16I ≥ 3x.

IV. Подведение итогов урока. Домашнее задание. (3 мин.)

2х 2 — 5IxI + 3x ≥ 0,

х 2 — 7IxI + 10
Ix 2 – 5xI
I2x 2 – 5xI ≤ 5x,
Ix + 3I > x 2 + 5x + 6,
Ix 2 + 6xI ≤ -3x.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Эффективное решение квадратных уравнений. Приемы устного решения.

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических.

урок по информатике в 9 классе по теме «Решение задач с конструкцией ветвление. Алгоритм решения квадратного уравнения»

Конспект и презентация к уроку в 9 классе по теме «Алгоритм решения квадратного уравнения».

План конспект урока по алгебре в 8 классе по теме «Решение квадратных уравнений содержащих параметры, решение нестандартных задач»

План конспект урока по алгебре в 8 классе по теме «Решение квадратных уравнений содержащих параметры, решение нестандартных задач&quot.

Конспект урока по теме: квадратные уравнения. Решение квадратных уравнений.

Урок в 8 классе по теме Учитель математики: Папшева Ю.А. Тема урока: Квадратные уравнения. Ре.

Решение уравнений, сводимых к решению квадратных уравнений

Тема «Решение квадратных уравнений» изучается в 8 классе, и она является одной из самых важных тем при изучении математики. В старших классах при изучении различных тем, мы возвращае.

Методические рекомендации к изучению темы: « Решение квадратных уравнений» с применением теоремы Виета для решения приведенного квадратного уравнения и полного квадратного уравнени

Решать квадратные уравнения учащимся приходится часто в старших классах, Решение иррациональных, показательных , логарифмических ,тригонометрических уравнений часто сводится к решени.

Решение задач по теме «Графические способы решения квадратных уравнений»

Цель урока: закрепить графический способ решения квадратных уравнений при решении задач практического содержания, формировать умения строить математические модели, совершенствование навыков пост.

Видео:Уравнения, сводящиеся к квадратным. Уравнение с модулемСкачать

Урок по теме «Квадратные уравнения, содержащие неизвестную под знаком модуля»

Разделы: Математика

Задача: провести повторение, обобщение и систематизацию знаний учащихся по теме “Квадратные уравнения. Квадратные уравнения, содержащие неизвестную под знаком модуля ”.

Тип урока: урок повторения, обобщения и систематизации знаний.

Организационные формы общения: работа в группах, индивидуальная работа.

Форма проведения урока: беседа с элементами самостоятельной работы учащихся, работа у доски, индивидуальная и групповая работа по выполнению учебных заданий.

Оборудование: ПК, проектор, экран.

I. Организационный момент.

(Приветствие учащихся и проверка готовности к уроку.)

– Квадратные уравнения в школьном курсе математики занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.), сегодня на уроке мы должны суметь применить все свои знания и умения к решению квадратных уравнений с параметром и модулем.

II. Постановка цели.

– Тема урока: “Квадратные уравнения, содержащие неизвестную под знаком модуля”. Сегодня у нас урок по решению квадратных уравнений, содержащих неизвестную под знаком модуля. Ребята, как можно сформулировать цель нашего урока исходя из его темы?

– Иными словами, повторить, обобщить и систематизировать весь предшествующий опыт решения квадратных уравнений, квадратных уравнений, содержащих неизвестную под знаком модуля. Для возможности выбора рационального пути решения.

– Итак, наша цель: обобщить опыт решения квадратных уравнений, квадратных уравнений с параметром и модулем, научиться выбирать рациональный путь решения.

III. Воспроизведение и коррекция опорных знаний:

– Прежде всего, вспомним некоторый, изученный материал. Приложение 1

– Выполним устно задания теста. Приложение 2

– Итак, весь необходимый материал повторили, я приглашаю вас на презентацию решения квадратных уравнений, содержащих неизвестную под знаком модуля. Для начала заполним карточки, которые лежат у каждого на столе. Приложение 3

Проверим. Возьмите в руки простой карандаш, сверим ответы.

Поднимите руки те, кто безошибочно справились с работой. Молодцы! Передайте свои заполненные карточки вперед.

IV. Обобщение и систематизация знаний, их применение для выполнения практических заданий:

1. Пример: Решите уравнение: x 2 -5│х│= 0.

Решение. Используя свойство модуля: |a| 2 =a 2 , перепишем данное уравнение в виде: │х│* (│х│– 5) = 0. Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю. Решив уравнение, имеем: х₁= 0, х_2,3= +5.

2. Пример: Существует ли на окружности, заданной уравнением (х-3) 2 + (у+1) 2 = 7, точка: а) с абсциссой, равной 1,5; б) с ординатой, равной – 3?

Решение. а) (у+1) 2 = 7 – (1,5 – 3) 2 >0 – такая точка существует; б) (х+3) 2 =7-(-3+1)>0-такая точка существует.

3.Пример: дано соотношение 2а 2 +4а + 2b 2 -4b – 5(a+1)(b-1) +4 = 0. Выразите b через а.

Решение. Имеем 2(а 2 +2a)+2(b 2 -2b) – 5(a+1)(b-1) +4 = 0;

2(a 2 +2a+1) +2(b 2 -2b+1)-5(a+1)(b-1)=0; 2(a+1) 2 -5(a+1)(b-1)+2(b-1) 2 =0.

Рассматривая это равенство, как квадратное уравнение относительно а+1, получим a+1 = 2(b-1) или a+1=(b-1)/2. Следовательно, b = (a+3)/2 или b= 2a+3.

4. Пример: Решите уравнение:│х 2 +х-3│=х.

Решение. Решим методом замены уравнения совокупностью, по определению модуля получаем систему:

5.Пример: Решите уравнение: │х+3│=│2х 2 +х-5│.

Решение. Решим методом замены уравнения совокупностью двух уравнений, по определению модуля получаем:

6.Пример: Решите уравнение: х 2 +(3-а)х-3а ‗0

Ответ: Нет решений при а = -3 и а = 4; при х = а данное уравнение имеет решение.

VI. Усвоение ведущих идей и основных теорий на основе широкой систематизации знаний:

7.Пример: Решите уравнение: │х-2│х 2 =10-5х.

Решение. Так как │х-2│х 2 =5(2-х), то х≤2.

Тогда уравнение примет вид (х-2)х 2 =5(2-х);

8. Пример: Решите уравнение:

Ответ: При b =7 или b = 2: один корень х = 2 b; при b = 1/2 или b = 3: один корень х = b – 1; при остальных b: два корня х = 2 b и х = b – 1.

VII. Оперирование ЗУН-ми в стандартных ситуациях:

9. Пример: Найдите сумму квадратов всех корней уравнения

Решение. Применив метод – введения новой переменной, решим уравнение. Пусть: t = │х│, получим уравнение t 2 – 3t + 1 = 0, имеющее два корня t₁ и t₂ (так как D>0). Очевидно, что корни t₁ и t₂ – положительны (t₁ + t₂ >0, t₁ * t₂ >0). Следовательно, по свойству модуля исходное уравнение, равносильно совокупности уравнений

имеет четыре корня: + t₁, + t₂. Их сумма квадратов t₁ 2 + (-t₁ ) 2 + t₂ 2 + (-t₂ ) 2 = 2(t₁ 2 +t₂ 2 ). Так как t₁ 2 +t₂ 2 = (t₁+t₂) 2 – 2 t₁ t₂ = 9 – 2*1 = 7, то искомая сумма квадратов всех корней равна 14.

10.Пример: При каком значении параметра а уравнение (а + 4х – х 2 -1)(а+1-│х – 2│) = 0 имеет три корня?

Решение. Данное уравнение равносильно совокупности уравнений:

Рассмотрим уравнение х 2 – 4х + 1 – а = 0.

Так как ¼ D = 4 – 1 + а = 3 + а, то при а > – 3 оно имеет два корня;

при а = – 3 – один корень; при а – 1 – два корня. При а – 1 каждое из уравнений имеет по два корня, симметричных относительно точки х₀ = 2. В этом случае х = 2 не является корнем, а общее число корней уравнений четно.

Итак, исходное уравнение имеет три корня лишь при а = – 1.

VIII. Пауза отдыха:

– Посмотрите на многообразие методов решения. Как, когда, сразу ли появилось такое многообразие? Как много вопросов…

Безусловно, человечество “додумалось” до всего не сразу и не в одночасье. Для этого потребовались долгие годы и даже столетия. Обратимся к историческому путеводителю. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилонии и Древнего Египта. Первое тысячелетие н.э. – Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат “Арифметика” содержит ряд задач, решаемых при помощи квадратных уравнений. В IX веке узбекский математик Аль-Хорезми в Трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь. Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению. И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым он заложил основы буквенной алгебры.

IX. Выполнение упражнений:

11. Одна из цифр двузначного числа на 3 меньше другой, а сумма квадратов этого числа и числа, полученного перестановкой его цифр, равна 1877. Найдите это число.

Решение. Пусть а – одна из цифр числа, тогда а + 3 – другая цифра. Исходное число имеет вид 10а + (а + 3) = 11а + 3.

После перестановки цифр получится число 10(а + 3) + а = 11а + 30. Согласно условию, получаем уравнение (10а + 3) 2 +(11а+30) 2 = 1877, откуда находим а = 1.

Ответ: 14 или 41.

X. Подведение итогов.

– Сегодня на уроке мы:

1) повторили определение квадратного уравнения;

2) рассмотрели виды квадратных уравнений и алгоритм решения квадратных уравнений, формулы для нахождения корней квадратного уравнения;

3) сформулировали теорему Виета и обратную ей теорему;

4) повторили определение модуля и параметра;

5) рассмотрели способы решения квадратных уравнений, содержащих параметр;

6) рассмотрели способы решения квадратных уравнений, содержащих модуль;

7) обобщили опыт решения квадратных уравнений с параметром и модулем;

8) научились выбирать наиболее рациональный метод решения квадратного уравнения с параметром и модулем.

– Оценки на уроке выставляются: – за теоретический опрос;

– за индивидуальную работу у доски;

– за работу по карточкам;

– за самостоятельную работу.

XI. Домашнее задание и его инструктаж:

М.Л. Галицкий, А.М.Гольдман, Л.И.Звавич. Сборник задач по алгебре для 8-9 классов. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Приложение 4

(Учащимся предлагается выполнить задание на приготовленных карточках)

Анищенко А.Г. и др. Имена в математике и информатике. – Брянск: РИО Брянского ИПКРО, 1995. – 96 с.
Балаян Э.Н. Как сдать ЕГЭ по математике на 100 баллов. – Ростов-на-Дону: Феникс, 2003. – 288 с.
Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Москва. 1996 и последующие издания.
Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа (методические рекомендации и дидактические материалы). – М.: Просвещение, 1986.
Глейзер Г.И. История математики в школе. VII-VIII классы. Пособие для учителей. – М.: Просвещение, 1982. – 240 с.
Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. Задания для проведения письменного экзамена по математики в 9 классе. Москва “Просвещение” 1994 и последующие издания.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дополнительные главы к школьному учебнику 8 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Под ред. Г.В.Дорофеева. Москва “Просвещение” 1997 и последующие издания.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Под ред. Г.В.Дорофеева. Москва “Просвещение” 1997 и последующие издания.
Макарычев Ю.Н., Миндюк Н.Г. Дидактические материалы по алгебре для 8 класса с углубленным изучением математики. Москва “Просвещение” 2001 и последующие издания.
Макарычев Ю.Н., Миндюк Н.Г. Дидактические материалы по алгебре для 9 класса с углубленным изучением математики. Москва “Просвещение” 2001 и последующие издания.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Квадратные уравнения с модулем.Скачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.