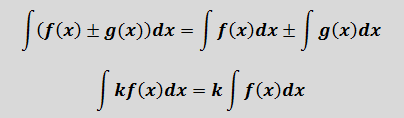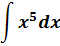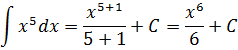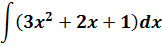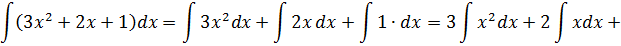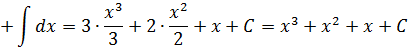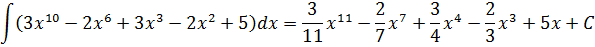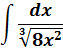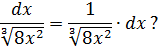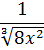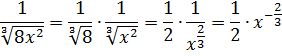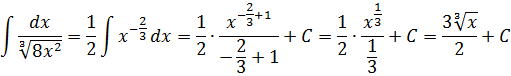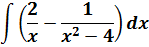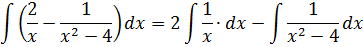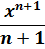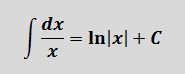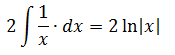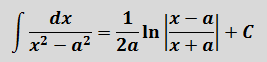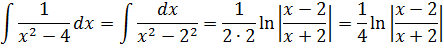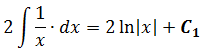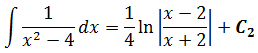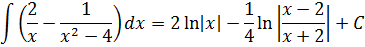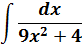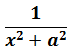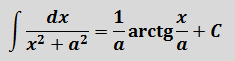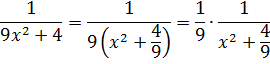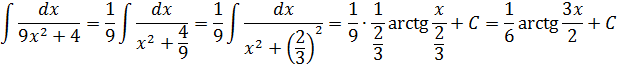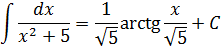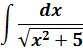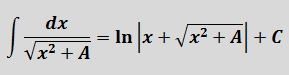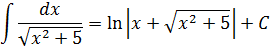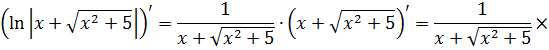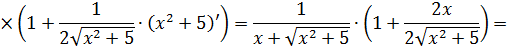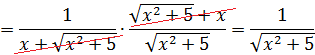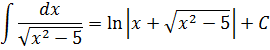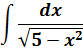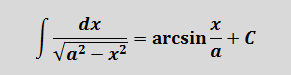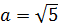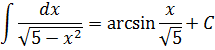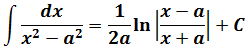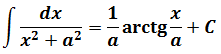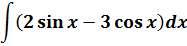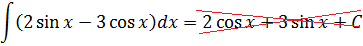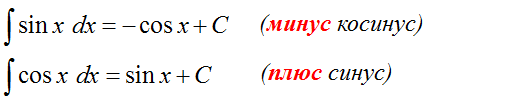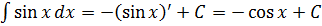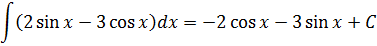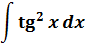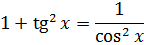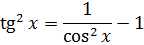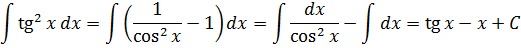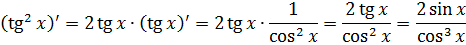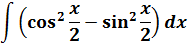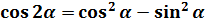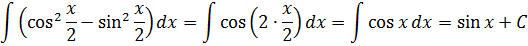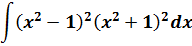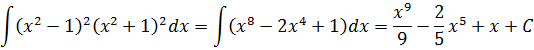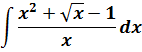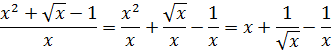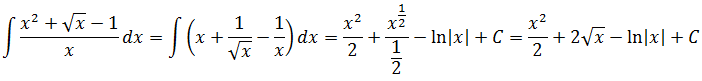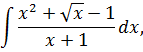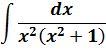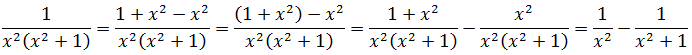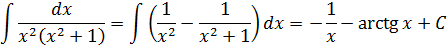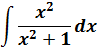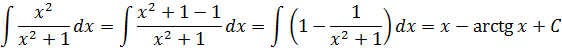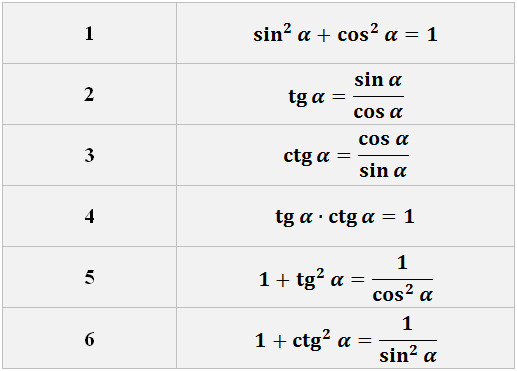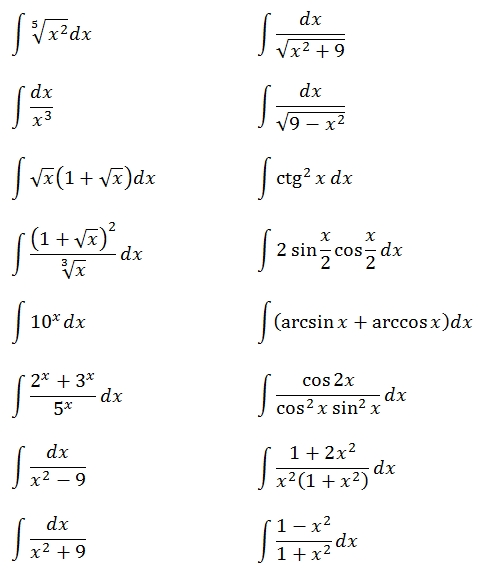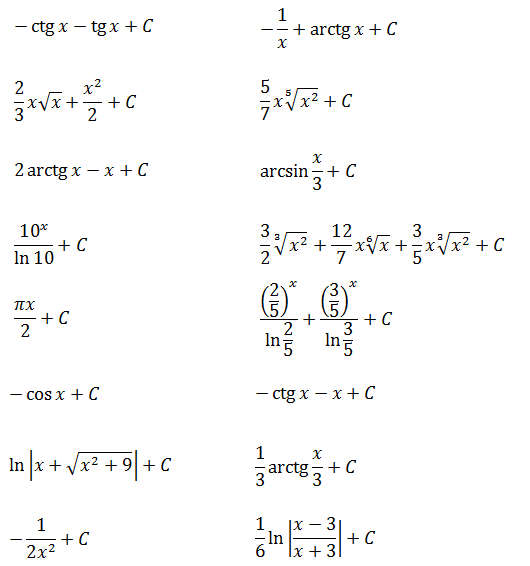Как решать интегральные уравнения для чайников

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решения интегральных уравнений онлайн

В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).

Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:

$$ (I) quad int_a^b K(x,s)u(s)ds = f(x),\ (II) quad u(x)=int_a^b K(x,s)u(s)ds + f(x). $$

В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:

$$ (I) quad int_a^x K(x,s)u(s)ds = f(x),\ (II) quad u(x)=int_a^x K(x,s)u(s)ds + f(x). $$

Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $lambda$ перед интегралом.

Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Примеры решений интегральных уравнений

Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+lambda A)x=y$ в гильбертовом пространстве $X$.

Задача 2. Найти собственные значения и собственные функции уравнения:

$$ y(x)=lambda int_0^1 (cos 2pi x +2x sin 2pi t +t sin pi x)y(t)dt. $$

Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.

Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.

Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.

Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^t^$.

Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $lambda$ (ограничиться случаем вещественных характеристических чисел).

$$ y(x)-lambda int_0^1 x y(t)dt = sin 2pi x. $$

Задача 8. Для симметричного ядра $$K(x,t) = frac sin |x-t| quad (0 le, x,t le pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.

Задача 9. Решить краевую задачу, используя функцию Грина

Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение

Видео:Дифференциальные уравнения. 11 класс.Скачать

Помощь с интегральными уравнениями

Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.

Видео:Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

Вычисление простейших неопределённых интегралов

И снова здравствуйте, друзья!

Как я и обещал, с этого урока мы начнём бороздить бескрайние просторы поэтического мира интегралов и приступим к решению самых разнообразных (порой, очень красивых) примеров. 🙂

Чтобы грамотно ориентироваться во всём интегральном многообразии и не заблудиться, нам потребуется всего четыре вещи:

1) Таблица интегралов. Все подробности о ней — в предыдущем материале. Как именно с ней работать — в этом.

2) Свойства линейности неопределённого интеграла (интеграл суммы/разности и произведения на константу).

3) Таблица производных и правила дифференцирования.

Да-да, не удивляйтесь! Без умения считать производные, в интегрировании ловить совершенно нечего. Согласитесь, бессмысленно, например, учиться делению, не умея умножать. 🙂 И очень скоро вы увидите, что без отточенных навыков дифференцирования не посчитать ни один сколь-нибудь серьёзный интеграл, выходящий за рамки элементарных табличных.

4) Методы интегрирования.

Их очень и очень много. Для конкретного класса функций — свой. Но среди всего их богатого разнообразия выделяется три базовых:

О каждом из них — в отдельных уроках.

А теперь, наконец, приступим к решению долгожданных примеров. Чтобы не скакать из раздела в раздел, я продублирую ещё разок весь джентльменский набор, который пригодится для нашей дальнейшей работы. Пусть весь инструментарий будет под рукой.)

Прежде всего, это таблица интегралов:

Кроме того, нам понадобятся базовые свойства неопределённого интеграла (свойства линейности):

Что ж, необходимая снаряга подготовлена. Пора в путь! 🙂

Прямое применение таблицы

В данном параграфе будут рассматриваться самые простые и безобидные примеры. Алгоритм здесь прост до ужаса:

1) Смотрим в таблицу и ищем нужную формулу (формулы);

2) Применяем свойства линейности (где требуется);

3) Осуществляем превращение по табличным формулам и прибавляем в конце константу С (не забываем!) ;

4) Записываем ответ.

Пример 1

Такой функции в нашей таблице нет. Зато есть интеграл от степенной функции в общем виде (вторая группа). В нашем случае n = 5. Вот и подставляем пятёрку вместо n и аккуратно считаем результат:

Разумеется, этот пример совсем примитивный. Чисто для знакомства.) Зато умение интегрировать степени позволяет легко считать интегралы от любых многочленов и прочих степенных конструкций.

Пример 2

Под интегралом сумма. Ну и ладно. У нас на этот случай есть свойства линейности. 🙂 Разбиваем наш интеграл на три отдельных, выносим все константы за знаки интегралов и считаем каждый по таблице (группа 1-2):

Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла! Конечно, после этого приходится её постоянно таскать за собой. А что делать…

Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить.)

Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к монстрам типа:

Многочлены — самые халявные функции в интегралах.) А уж в диффурах, в физике, в сопромате и прочих серьёзных дисциплинах интегрировать многочлены придётся постоянно. Привыкайте.)

Следующий примерчик будет чуть покруче.

Пример 3

Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:

Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.

Замечание: в этом уроке множитель dx в процессе интегрирования пока никак не участвует, и мы на него пока что мысленно «забиваем». 🙂 Работаем только с подынтегральной функцией. Но забывать про него не будем. Совсем скоро, буквально на следующем уроке, посвящённом подведению функции под знак дифференциала , мы про него вспомним. И ощутим всю важность и мощь этого значка в полную силу!)

А пока наш взор обращён на подынтегральную функцию

Не очень похоже на степенную функцию, но это она. 🙂 Если вспомнить школьные свойства корней и степеней, то вполне можно преобразовать нашу функцию:

А икс в степени минус две трети — это уже табличная функция! Вторая группа, n=-2/3. А константа 1/2 нам не помеха. Выносим её наружу, за знак интеграла, и прямо по формуле считаем:

В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:

Заменяем дроби степенями с отрицательными показателями;

Заменяем корни степенями с дробными показателями.

А вот в окончательном ответе переход от степеней обратно к дробям и корням — дело вкуса. Лично я перехожу обратно — так эстетичнее, что ли.

И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт — что в числитель, а что знаменатель.

Что? Надоели уже скучные степенные функции? Ну ладно! Берём быка за рога!

Пример 4

Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго.) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:

Первый интеграл — обычная степенная функция, (2-я группа, n = -1): 1/x = x -1 .

Традиционная наша формула для первообразной степенной функции

здесь не работает, но зато у нас для n = -1 есть достойная альтернатива — формула с натуральным логарифмом. Вот эта:

Тогда, согласно этой формуле, первая дробь проинтегрируется так:

А вторая дробь — тоже табличная функция! Узнали? Да! Это седьмая формула с «высоким» логарифмом:

Константа «а» в этой формуле равна двойке: a=2.

Важное замечание: Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно.) Строго говоря, константу надо писать после каждого отдельного интегрирования — хоть промежуточного, хоть окончательного: так уж неопределённый интеграл требует…)

Например, после первого интегрирования я должен был бы написать:

После второго интегрирования:

Но вся фишка в том, что сумма/разность произвольных констант — это тоже некоторая константа! В нашем случае для окончательного ответа нам надо из первого интеграла вычесть второй. Тогда у нас получится разность двух промежуточных констант:

И мы имеем полное право эту самую разность констант заменить одной константой! И просто переобозначить её привычной нам буквой «С». Вот так:

Вот и приписываем эту самую константу С к окончательному результату и получаем ответ:

Да-да, дроби они такие! Многоэтажные логарифмы при их интегрировании — самое обычное дело. Тоже привыкаем.)

Запоминаем:

При промежуточном интегрировании нескольких слагаемых константу С после каждого из них можно не писать. Достаточно включить её в окончательный ответ всего примера. В самом конце.

Следующий пример тоже с дробью. Для разминки.)

Пример 5

В таблице, понятное дело, такой функции нет. Но зато есть похожая функция:

Это самая последняя, восьмая формула. С арктангенсом. 🙂

И нам сам бог велел подстроить наш интеграл под эту формулу! Но есть одна проблемка: в табличной формуле перед х 2 никакого коэффициента нету, а у нас — девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби.)

А новая дробь — уже нужная нам табличная функция под номером 8! Здесь а 2 =4/9. Или а=2/3.

Всё. Выносим 1/9 за знак интеграла и пользуемся восьмой формулой:

Вот такой ответ. Этот пример, с коэффициентом перед х 2 , я специально так подобрал. Чтобы ясно было, что делать в таких случаях. 🙂 Если перед х 2 никакого коэффициента нет, то такие дроби тоже будут в уме интегрироваться.

Здесь а 2 = 5, поэтому само «а» будет «корень из пяти». В общем, вы поняли.)

А теперь немного видоизменим нашу функцию: напишем знаменатель под корнем.) Вот такой интеграл теперь будем брать:

Пример 6

В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования, да.) Опять лезем в таблицу и ищем подходящую. Корни у нас есть в формулах 5-й и 6-й групп. Но в шестой группе под корнями только разность. А у нас — сумма. Значит, работаем по пятой формуле, с «длинным» логарифмом:

Число А у нас — пятёрка. Подставляем в формулу и получаем:

И все дела. Это ответ. Да-да, так просто!)

Если закрадываются сомнения, то всегда можно (и нужно) проверить результат обратным дифференцированием. Проверим? А то вдруг, лажа какая-нибудь?

Дифференцируем (на модуль внимания не обращаем и воспринимаем его как обычные скобки):

Кстати, если в подынтегральной функции под корнем поменять знак с плюса на минус, то формула для интегрирования останется той же самой. Не случайно в таблице под корнем стоит плюс/минус. 🙂

Важно! В случае минуса, на первом месте под корнем должно стоять именно х 2 , а на втором — число. Если же под корнем всё наоборот, то и соответствующая табличная формула будет уже другая!

Пример 7

Под корнем снова минус, но х 2 с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формулка.) Формула номер шесть, с ней мы ещё не работали:

А вот теперь — аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A. Здесь же пятёрка будет выступать уже в роли числа а 2 !

Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:

И теперь пример решается в одно действие. 🙂

Вот так вот! Всего лишь поменялись местами слагаемые под корнем, а результат интегрирования изменился существенно! Логарифм и арксинус… Так что, пожалуйста, не путайте эти две формулы! Хотя подынтегральные функции и очень похожи…

В табличных формулах 7-8 перед логарифмом и арктангенсом присутствуют коэффициенты 1/(2а) и 1/а соответственно. И в тревожной боевой обстановке при записи этих формул даже закалённые учёбой ботаны частенько путаются, где просто 1/а, а где 1/(2а). Вот вам простой приёмчик для запоминания.

в знаменателе подынтегральной функции стоит разность квадратов х 2 — а 2 . Которая, согласно боянной школьной формуле, раскладывается как (х-а)(х+а). На два множителя. Ключевое слово — два. И эти две скобки при интегрировании идут в логарифм: с минусом вверх, с плюсом — вниз.) И коэффициент перед логарифмом тоже 1/(2а).

А вот в формуле №8

в знаменателе дроби стоит сумма квадратов. Но сумма квадратов x 2 +a 2 неразложима на более простые множители. Поэтому, как ни крути, в знаменателе так и останется один множитель. И коэффициент перед арктангенсом тоже будет 1/а.

А теперь для разнообразия проинтегрируем что-нибудь из тригонометрии.)

Пример 8

Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же радостно ответ пишет и… приехали. 🙂

Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!

Но!

Поскольку производные народ обычно худо-бедно помнит, то, чтобы не путаться в знаках, приём для запоминания интегралов тут очень простой:

Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.

Например, мы ещё со школы знаем, что производная синуса равна косинусу:

Тогда для интеграла от того же синуса будет справедливо:

И всё.) С косинусом то же самое.

Исправляем теперь наш пример:

Предварительные элементарные преобразования подынтегральной функции

До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)

Конечно, мы делали кое-какие простенькие преобразования — множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)

А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной. 🙂

Продолжим развлекаться с тригонометрией.

Пример 9

Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:

Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:

Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!

А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать — применять формулу производной сложной функции:

И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.

А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование — более творческий процесс, нежели дифференцирование. Искусство, я бы даже сказал. 🙂 И это ещё не самый сложный пример. То ли ещё будет!

Пример 10

Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно откопать весьма и весьма полезную формулу косинуса двойного угла:

Вот и применяем эту формулу к нашей подынтегральной функции. В роли «альфа» у нас х/2.

Эффект потрясающий, правда?

Эти два примера наглядно показывают, что предварительное преобразование функции перед интегрированием вполне допускается и порой колоссально облегчает жизнь! И в интегрировании эта процедура (преобразование подынтегральной функции) на порядок более оправдана, чем при дифференцировании. В дальнейшем всё увидите.)

Разберём ещё парочку типовых преобразований.

Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.

Обычные банальные школьные преобразования. Но порой только они и спасают, да.)

Пример 11

Если бы мы считали производную, то никаких проблем: формула производной произведения и — вперёд. Но стандартной формулы для интеграла от произведения не существует. И единственный выход здесь — раскрыть все скобки, чтобы под интегралом получился многочлен. А уж многочлен мы как-нибудь проинтегрируем.) Но скобки раскрывать тоже будем с умом: формулы сокращённого умножения — штука мощная!

(x 2 — 1) 2 (x 2 + 1) 2 = ((x 2 — 1)(x 2 + 1)) 2 = ((x 2 ) 2 — 1 2 ) 2 = (x 4 — 1) 2 = x 8 — 2x 4 + 1

А теперь считаем:

Пример 12

Опять же, стандартной формулы для интеграла от дроби не существует. Однако в знаменателе подынтегральной дроби стоит одинокий икс. Это в корне меняет ситуацию.) Поделим почленно числитель на знаменатель, сведя нашу жуткую дробь к безобидной сумме табличных степенных функций:

Особо комментировать процедуру интегрирования степеней не буду: не маленькие уже.)

Интегрируем сумму степенных функций. По табличке.)

Вот и все дела.) Кстати, если бы в знаменателе сидел не икс, а, скажем, х+1, вот так:

то этот фокус с почленным делением уже так просто не прошёл бы. Именно из-за наличия корня в числителе и единицы в знаменателе. Пришлось бы замену вводить и избавляться от корня. Но такие интегралы гораздо сложнее. О них — в других уроках.

Видите! Стоит только чуть-чуть видоизменить функцию — тут же меняется и подход к её интегрированию. Порой кардинально!) Нету чёткой стандартной схемы. К каждой функции — свой подход. Иногда даже уникальный.)

В некоторых случаях преобразования в дробях ещё более хитрые.

Пример 13

А здесь как можно свести интеграл к набору табличных? Здесь можно ловко извернуться добавлением и вычитанием выражения x 2 в числителе дроби с последующим почленным делением. Очень искусный приём в интегралах! Смотрите мастер-класс! 🙂

И теперь, если заменить исходную дробь на разность двух дробей, то наш интеграл распадается на два табличных — уже знакомую нам степенную функцию и арктангенс (формула 8):

Ну, что тут можно сказать? Вау!

Этот трюк с добавлением/вычитанием слагаемых в числителе — очень популярен в интегрировании рациональных дробей. Очень! Рекомендую взять на заметку.

Пример 14

Здесь тоже рулит эта же технология. Только добавлять/вычитать надо единичку, чтобы из числителя выделить выражение, стоящее в знаменателе:

Вообще говоря, рациональные дроби (с многочленами в числителе и знаменателе) — отдельная очень обширная тема. Дело всё в том, что рациональные дроби — один из очень немногих классов функций, для которых универсальный способ интегрирования существует. Метод разложения на простейшие дроби вкупе с методом неопределённых коэффициентов. Но способ этот очень трудоёмкий и обычно применяется как тяжёлая артиллерия. Ему будет посвящён не один урок. А пока что тренируемся и набиваем руку на простых функциях.

Подытожим сегодняшний урок.

Сегодня мы подробно рассмотрели, как именно пользоваться таблицей, со всеми нюансами, разобрали множество примеров (и не самых тривиальных) и познакомились с простейшими приёмами сведения интегралов к табличным. И так мы теперь будем поступать всегда. Какая бы страшная функция ни стояла под интегралом, с помощью самых разнообразных преобразований мы будем добиваться того, чтобы, рано или поздно, наш интеграл, так или иначе, свёлся к набору табличных.

Несколько практических советов.

1) Если под интегралом дробь, в числителе которой сумма степеней (корней), а в знаменателе — одинокая степень икса, то используем почленное деление числителя на знаменатель. Заменяем корни степенями с дробными показателями и работаем по формулам 1-2.

2) В тригонометрических конструкциях в первую очередь пробуем базовые формулы тригонометрии — двойного/тройного угла, основные тригонометрические тождества:

Может очень крупно повезти. А может и нет…

3) Где нужно (особенно в многочленах и дробях), применяем формулы сокращённого умножения:

(a+b) 2 = a 2 +2ab+b 2

4) При интегрировании дробей с многочленами пробуем искусственно выделить в числителе выражение(я), стоящее(щие) в знаменателе. Очень часто дробь упрощается и интеграл сводится к комбинации табличных.

Ну что, друзья? Я вижу, интегралы вам начинают нравиться. 🙂 Тогда набиваем руку и решаем примеры самостоятельно.) Сегодняшнего материала вполне достаточно, чтобы успешно с ними справиться.

Что? Не знаете, как интегрировать арксинус/арккосинус ? Да! Мы этого ещё не проходили.) Но здесь их напрямую интегрировать и не нужно. И да поможет вам школьный курс!)

Ответы (в беспорядке):

Для лучших результатов настоятельно рекомендую приобрести сборник задач по матану Г.Н. Бермана. Классная штука!

Видео:Как решают уравнения в России и СШАСкачать

Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница

Видео:Интеграл: Азы интегрирования. Высшая математикаСкачать

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

К сожалению, так сложилось, что многим (и мне) она, порой кажется, слишком сложной, недоступной, наукой для избранных. Между тем, так только кажется ! Безусловно, она требует интеллектуального напряжения, памяти, воображения и много чего ещё, как и многие другие интеллектуальные занятия.

Отличительными особенностями её являются:

использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),

логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),

последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),

высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин

Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы

Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)

Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук

Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными

Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее

Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Во введении к книге «Развитие понятия интеграла» известный историк математики профессор Фёдор Андреевич Медведев так охарактеризовал сущность интегрирования и процесс его развития в науке «. Интегрирование представляет собой абстрактное выражение разнообразнейших способов измерения величин, и по мере вовлечения в человеческое познание всё новых и новых объектов реальной действительности математики создают всё более и более общие схемы интеграционных процессов с тем, чтобы охватить всё расширяющийся круг объектов, подлежащих измерению» [1].

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

Видео:Простейшие интегральные уравненияСкачать

2. Геометрический и аналитико-алгебраический смысл интегрирования

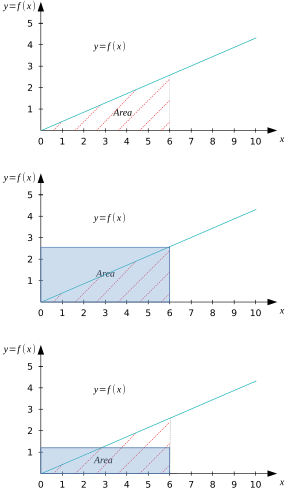
Естественным образом, возникает два вида задач, которые отражают два смысла интегрирования: — геометрический и аналитико-алгебраический. Первый — отыскание площади плоской фигуры под произвольной кривой (квадратура) и отыскание объёма (кубатура). Второй — подсчёт суммарного значения некой переменной величины [2], которая изменяется, принимает различные значения сообразно единицам времени, длины и т.д.

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].

В случае с вещественными числами.

Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.

Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.

В случае с отрицательными числами (-2,3 × 4,3), умножение — сумма произведений и разворот числовой оси или иными словами отражение суммарного значения произведения — в данном случае числа 9,89 относительно начала отсчёта, то есть числа ноль, в результате получаем -9,89.

В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».

Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

Видео:Зачем нужен ИНТЕГРАЛ. Объяснение смыслаСкачать

3. Интуитивные способы отыскания значения интеграла

Итак, каким же образом вычислить интегральную сумму ? Можно попробовать несколько способов:

Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).

Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение

Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).

Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

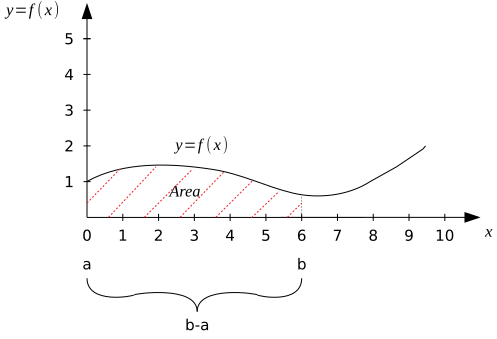
Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

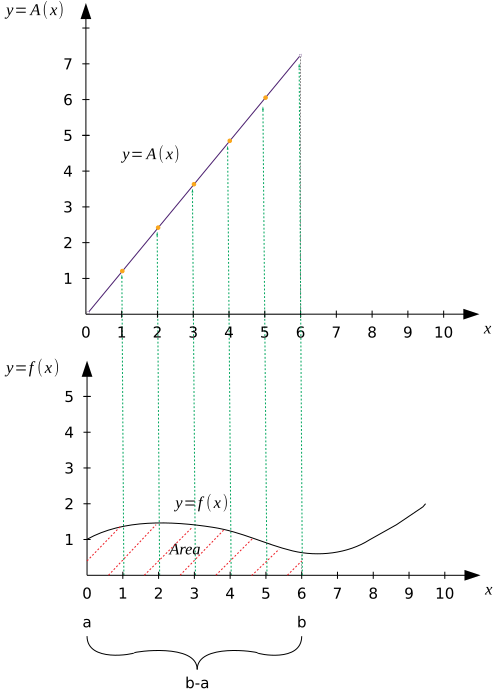
Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[1]. Медведев Ф.А. Развитие понятия интеграла. — М.: Наука, 1974. С. 4

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .

[7]. То есть . К примеру, пусть функция задана выражением . Тогда, при , , а значение . Если. Тогда, при , , а значение .

[8]. Пусть имеется точка, число 7 и 10, чтобы найти величину промежутка между этими значениями надо найти разность то есть 10 — 7 = 3.

📽️ Видео

Интегральные уравнения ВольтерраСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Определенный интеграл. 11 класс.Скачать

Как решать квадратные уравнения для чайниковСкачать

ИНТЕГРАЛ С НУЛЯ | определенный интеграл | ТАБЛИЦА ИНТЕГРАЛОВ | сумма РиманаСкачать

Решить интегральное уравнениеСкачать