Как решать графически уравнения синус (3 видео)

Решение тригонометрических уравнений графически

Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.

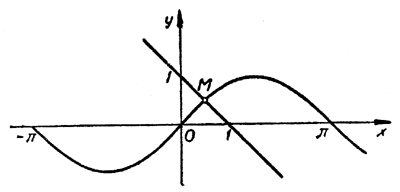
Пусть, например, нужно решить уравнение

На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х

Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:

Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5

следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x₀должен быть меньше, чем 0,6. Теперь уже мы знаем, что x₀ находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1

С помощью таблиц можно найти приближенное значение x₀ и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала

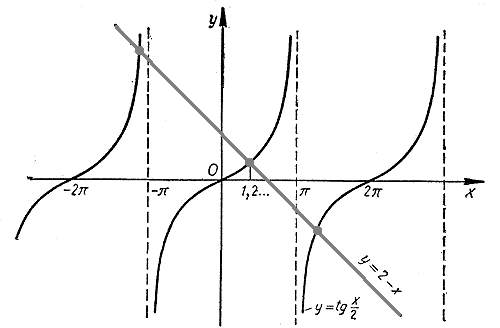
Графики функций у = tg x /₂ и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х₀. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.

Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /₂ и у = 2 — х в окрестности точки х = 1,2.

x	1,2	1,3
y=tg x/2	0,6841	0,7602
y=2-x	0,8000	0,7000
tg x/2-(2-x)	-0,1159	0,0602

Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /₂ — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х₀ ≈ 1,2 (с недостатком) или х₀ ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25

Содержание

Функция y = sin x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
п.2. Свойства функции y=sinx⁡
п.3. Примеры
Способы решения тригонометрических уравнений. 10-й класс
1 урок
2 урок (урок-лекция)
🔥 Видео

Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .
Часть синусоиды для 0≤x≤2π называют волной синусоиды .
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .

п.2. Свойства функции y=sinx⁡

1. Область определения (xinmathbb) — множество действительных чисел.

2. Функция ограничена сверху и снизу

Область значений (yin[-1;1])

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения (y_=1) достигаются в точках

Минимальные значения (y_=-1) достигаются в точках

Нули функции (y_=sinx_0=0) достигаются в точках (x_0=pi k)

6. Функция возрастает на отрезках

$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$

Функция убывает на отрезках

$$ fracpi2+2pi kleq xleqfrac+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:

a) (left[fracpi6; fracright]) $$ y_=sinleft(fracpi6right)=frac12, y_=sinleft(fracpi2right)=1 $$ б) (left[frac; fracright]) $$ y_=sinleft(fracright)=-1, y_=sinleft(fracright)=frac12 $$

Пример 2. Решите уравнение графически:
a) (sinx=3x)

Один корень: x = 0

б) (sinx=2x-2pi)

Один корень: x = π

в) (sinx-sqrt=0)
(sinx=sqrt)

Один корень: x = π

г*) (sinx=left(x-fracpi2right)^2-frac)
(y=left(x-fracpi2right)^2-frac) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -fracright)) (см. §29 справочника для 8 класса)

Два корня: (x_1=0, x_2=pi)

Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$

(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) — исходная функция поднимается вверх на 2. Область значений (yin[1;3]).

Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac $$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) — период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac) — период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Способы решения тригонометрических уравнений. 10-й класс

Разделы: Математика

Класс: 10

«Уравнения будут существовать вечно».

Цели урока:

Образовательные:
- углубление понимания методов решения тригонометрических уравнений;
- сформировать навыки различать, правильно отбирать способы решения тригонометрических уравнений.
Воспитательные:
- воспитание познавательного интереса к учебному процессу;
- формирование умения анализировать поставленную задачу;
- способствовать улучшению психологического климата в классе.
Развивающие:
- способствовать развитию навыка самостоятельного приобретения знаний;
- способствовать умению учащихся аргументировать свою точку зрения;

Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.

1 урок

I. Актуализация опорных знаний

Устно решить уравнения:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –;
6) sinx = ;
7) tgx = ;
8) cos 2 x – sin 2 x = 0

1) х = 2к;
2) х = ± + 2к;
3) х =± + 2к;
4) х = к;
5) х = (–1) + к;
6) х = (–1) + 2к;
7) х = + к;
8) х = + к; к Z.

II. Изучение нового материала

– Сегодня мы с вами рассмотрим более сложные тригонометрические уравнения. Рассмотрим 10 способов их решения. Далее будет два урока для закрепления, и на следующий урок будет проверочная работа. На стенде «К уроку» вывешены задания, аналогичные которым будут на проверочной работе, надо их прорешать до проверочной работы. (Накануне, перед проверочной работой, вывесить на стенде решения этих заданий).

Итак, переходим к рассмотрению способов решения тригонометрических уравнений. Одни из этих способов вам, наверное, покажутся трудными, а другие – лёгкими, т.к. некоторыми приёмами решения уравнений вы уже владеете.

Четверо учащихся класса получили индивидуальное задание: разобраться и показать вам 4 способа решения тригонометрических уравнений.

(Выступающие учащиеся заранее подготовили слайды. Остальные учащиеся класса записывают основные этапы решения уравнений в тетрадь.)

1 ученик: 1 способ. Решение уравнений разложением на множители

sin 4x = 3 cos 2x

Для решения уравнения воспользуемся формулой синуса двойного угла sin 2 = 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Произведение этих множителей равно нулю, если хотя бы один из множителей будет равен нулю.

2x = + к, к Z или sin 2x = 1,5 – нет решений, т.к | sin| 1
x = + к; к Z.
Ответ: x = + к , к Z.

2 ученик. 2 способ. Решение уравнений преобразованием суммы или разности тригонометрических функций в произведение

cos 3x + sin 2x – sin 4x = 0.

Для решения уравнения воспользуемся формулой sin– sin = 2 sin сos

cos 3x + 2 sin сos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. Полученное уравнение равносильно совокупности двух уравнений:

Множество решений второго уравнения полностью входит во множество решений первого уравнения. Значит

Ответ:

3 ученик. 3 способ. Решение уравнений преобразованием произведения тригонометрических функций в сумму

sin 5x cos 3x = sin 6x cos2x.

Для решения уравнения воспользуемся формулой

Ответ:

4 ученик. 4 способ. Решение уравнений, сводящихся к квадратным уравнениям

3 sin x – 2 cos 2 x = 0,
3 sin x – 2 (1 – sin 2 x ) = 0,
2 sin 2 x + 3 sin x – 2 = 0,

Пусть sin x = t, где | t |. Получим квадратное уравнение 2t 2 + 3t – 2 = 0,

. Таким образом . не удовлетворяет условию | t |.

Значит sin x = . Поэтому .

Ответ:

III. Закрепление изученного по учебнику А. Н. Колмогорова

1. № 164 (а), 167 (а) (квадратное уравнение)
2. № 168 (а) (разложение на множители)
3. № 174 (а) (преобразование суммы в произведение)
4. (преобразование произведения в сумму)

(В конце урока показать решение этих уравнений на экране для проверки)

№ 164 (а)

2 sin 2 x + sin x – 1 = 0.
Пусть sin x = t, | t | 1. Тогда
2 t 2 + t – 1 = 0, t = – 1, t= . Откуда

Ответ: –.

№ 167 (а)

3 tg 2 x + 2 tg x – 1 = 0.

Пусть tg x = 1, тогда получим уравнение 3 t 2 + 2 t – 1 = 0.

Ответ:

№ 168 (а )

Ответ:

№ 174 (а )

Ответ:

Решить уравнение:

Ответ:

2 урок (урок-лекция)

IV. Изучение нового материала (продолжение)

– Итак, продолжим изучение способов решения тригонометрических уравнений.

5 способ. Решение однородных тригонометрических уравнений

Уравнения вида a sin x + b cos x = 0, где a и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.

sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к. , если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству sin 2 x + cos 2 x = 1.

Получим tg x – 1 = 0.

Ответ:

Уравнения вида a sin 2 x + bcos 2 x + c sin x cos x = 0 , где a, b, c –некоторые числа, называются однородными уравнениями второй степени относительно sin x или cos x.

sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Разделим обе части уравнения на cos x, при этом потери корня не произойдёт, т.к. cos x = 0 не является корнем данного уравнения.

tg 2 x – 3tg x + 2 = 0.

Пусть tg x = t. D = 9 – 8 = 1.

тогда Отсюда tg x = 2 или tg x = 1.

В итоге x = arctg 2 + , x =

Ответ: arctg 2 + ,

Рассмотрим ещё одно уравнение: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Преобразуем правую часть уравнения в виде 2 = 2 · 1 = 2 · (sin 2 x + cos 2 x). Тогда получим:
3sin 2 x – 3sin x cos x + 4cos 2 x = 2 · (sin 2 x + cos 2 x),
3sin 2 x – 3sin x cos x + 4cos 2 x – 2sin 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (Получили 2 уравнение, которое уже разобрали).

Ответ: arctg 2 + k,

6 способ. Решение линейных тригонометрических уравнений

Линейным тригонометрическим уравнением называется уравнение вида a sin x + b cos x = с, где a, b, c – некоторые числа.

Рассмотрим уравнение sin x + cos x = – 1.
Перепишем уравнение в виде:

Учитывая, что и, получим:

Ответ:

7 способ. Введение дополнительного аргумента

Выражение a cos x + b sin x можно преобразовать:

(это преобразование мы уже ранее использовали при упрощении тригонометрических выражений)

Введём дополнительный аргумент – угол такой, что

Тогда

Рассмотрим уравнение: 3 sinx + 4 cosx = 1.

Учтём, что . Тогда получим

0,6 sin x + 0,8 cosx = 1. Введём дополнительный аргумент – угол такой, что , т.е. = arcsin 0,6. Далее получим

Ответ: – arcsin 0,8 + +

8 способ. Уравнения вида Р

Такого рода уравнения удобно решать при помощи введения вспомогательной переменной t = sin x ± cosx. Тогда 1 ± 2 sinx cosx = t 2 .

Решить уравнение: sinx + cosx + 4 sinx cosx – 1 = 0.

Введём новую переменную t = sinx + cosx, тогда t 2 = sin 2 x + 2sin x cos x + cos 2 = 1 + 2 sin x cos x Откуда sin x cos x = . Следовательно получим:

t + 2 (t 2 – 1) – 1 = 0.
2 t 2 + t – 2 – 1 = 0,
2 t 2 + t – 3 = 0..Решив уравнение, получим = 1, =.

sinx + cosx = 1 или sinx + cosx =

Ответ:

9 способ. Решение уравнений, содержащих тригонометрические функции под знаком радикала.

Решить уравнение:

В соответствии с общим правилом решения иррациональных уравнений вида, запишем систему, равносильную исходному уравнению:

Решим уравнение 1 – cos x = 1 – cos 2 x.

1 – cos x = 1 – cos 2 x,
1 – cos x – (1 – cos x) (1 + cos x) = 0,
(1 – cos x) (1 – 1 – cos x) = 0,
– (1 – cos x) cos x = 0.

Условию удовлетворяют только решения

Ответ:

10 способ. Решение уравнений с использованием ограниченности тригонометрических функций y = sin x и y = cos x.

Решить уравнение: sin x + sin 9x = 2.
Так как при любых значениях х sin x 1, то данное уравнение равносильно системе:

Решение системы

Ответ:

V. Итог урока

Таким образом мы сегодня рассмотрели 10 различных способов решения тригонометрических уравнений. Безусловно, многие из приведённых задач могут быть решены несколькими способами.

(Пятерым наиболее подготовленным учащимся , а также всем желающим дать индивидуальное творческое задание: найти различные способы решения тригонометрического уравнения sinx + cosx = 1 )

Домашнее задание: № 164 -170 (в, г).