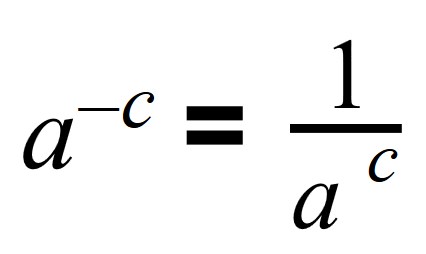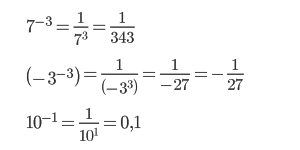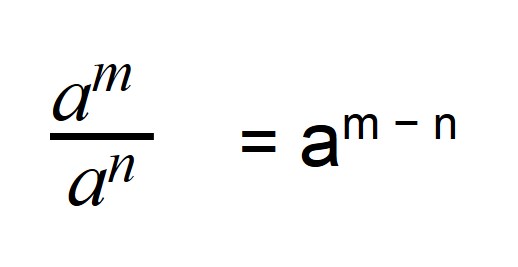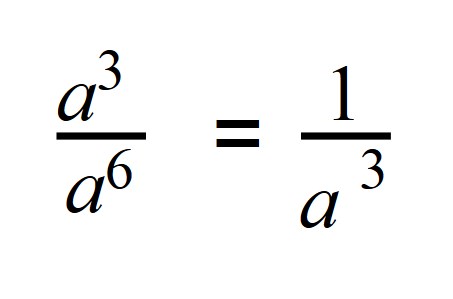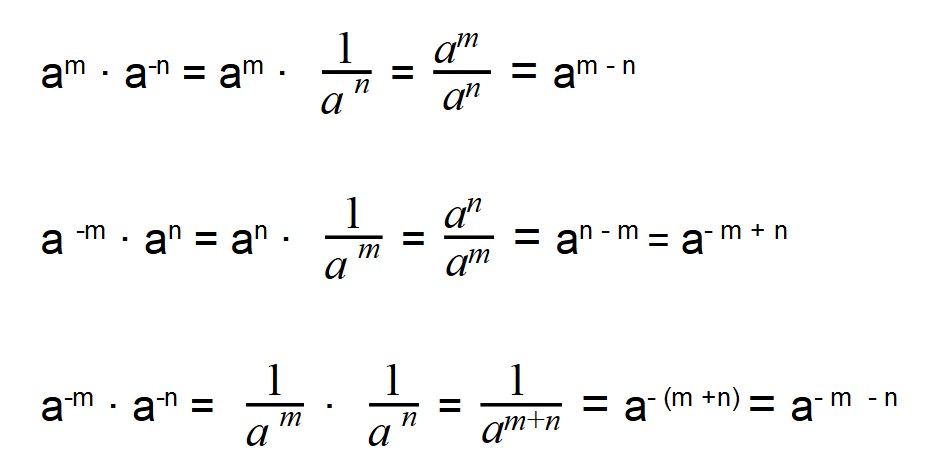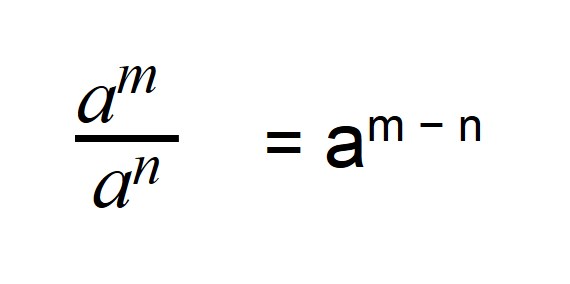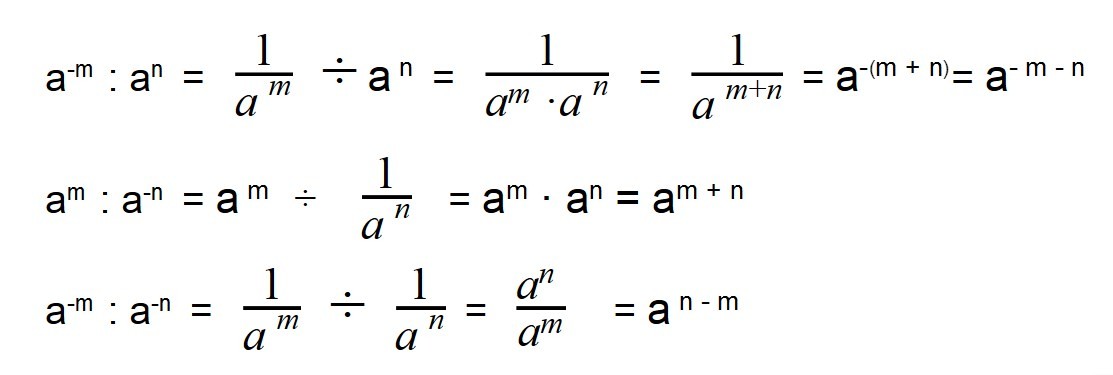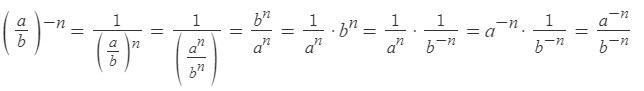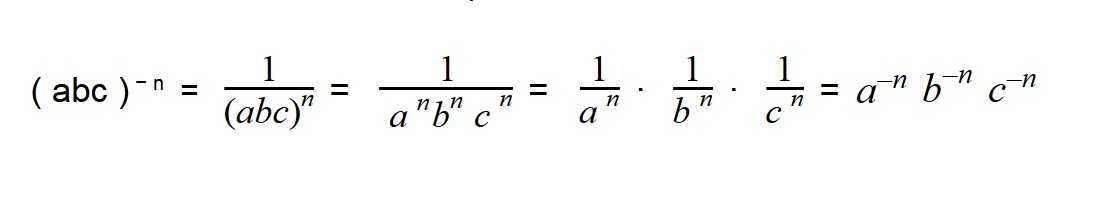Как решать дробные уравнения с отрицательной степенью

Видео:СтепениСкачать

Степень с отрицательным показателем

Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.

Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.

Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

Пример 1. Замените дробь степенью с отрицательным показателем:

Пример 2. Представьте в виде степени с отрицательным показателем:

Видео:ОТРИЦАТЕЛЬНЫЕ СТЕПЕНИ ЧИСЕЛ ДЛЯ ЕГЭ #shorts #егэ #огэ #математика #степени #отрицательныестепениСкачать

Действия над степенями с отрицательными показателями

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:

Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:

Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:

При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Рациональные уравнения с примерами решения

Содержание:

Видео:Степень с отрицательным дробным показателем. ПримерыСкачать

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Видео:ДРОБНЫЕ СТЕПЕНИ ЧАСТЬ I #shorts #математика #егэ #огэ #дробныестепениСкачать

Отрицательная степень

О чем эта статья:

7 класс, 8 класс

Видео:Как решать уравнения с дробной степеньюСкачать

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

Например, a n — степень, где:

• a — основание степени,
• n — показатель степени.

Читается такое выражение как a в степени n.

Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 3 = 2 · 2 · 2, где:

• 2 — основание степени,
• 3 — показатель степени.

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:8 класс, 6 урок, Степень с целым отрицательным показателемСкачать

Степень с отрицательным показателем

Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:

К примеру, 4 в минус 2 степени — это 1/4 2 , 2 в минус 3 степени — это 1/2 3 , 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 или 0,1.

Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины. Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10 -9 ). В школьной программе такие величины — редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.

Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.

Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.

Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:

a 3 : a 6 =a 3 — 6 = a -3

Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:

Видео:Как решать уравнения с дробью? #shortsСкачать

Действия с отрицательными степенями

Умножение отрицательных степеней

При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:

a m · a n = a m + n

Деление отрицательных степеней

При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:

Возведение дроби в отрицательную степень

Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:

Возведение произведения в отрицательную степень

Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:

🌟 Видео

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Алгебра 8 класс 15 октября Отрицательная степеньСкачать

Сокращаем дроби со степенями №2. Алгебра 8 класс.Скачать

Отрицательная степень числа - Разбор задания из ОГЭСкачать

Степень с дробным показателем. ВведениеСкачать

Как возводить в дробную степень?!🥵Скачать

СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМСкачать

Дробно рациональные уравнения. Алгебра, 9 классСкачать

Математика| СтепениСкачать

СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ | алгебра 7 | ПОКАЗАТЕЛЬ СТЕПЕНИ | свойства степенейСкачать

Решить уравнение. Степень с целым отрицательным показателемСкачать

Как решают уравнения в России и СШАСкачать