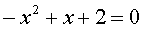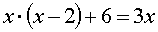Как решать дробные уравнения через дискриминант (2 видео)

Как решать квадратные уравнения? Дискриминант.

Поработаем с квадратными уравнениями. Это очень популярные уравнения! В самом общем виде квадратное уравнение выглядит так:

Как решать квадратные уравнения? Если перед вами квадратное уравнение именно в таком виде, дальше уже всё просто. Вспоминаем волшебное слово дискриминант. Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении. Итак, формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня – и есть тот самый дискриминант. Как видим, для нахождения икса, мы используем только a, b и с. Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в это формулу и считаем. Подставляем со своими знаками! Например, для первого уравнения а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Какие случаи возможны при использовании этой формулы? Всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас одно решение. Строго говоря, это не один корень, а два одинаковых. Но это играет роль в неравенствах, там мы поподробнее вопрос изучим.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…
Самые распространённые ошибки – путаница со знаками значений a, b и с. Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте!

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится. Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Итак, как решать квадратные уравнения через дискриминант мы вспомнили. Или научились, что тоже неплохо. Умеете правильно определять a, b и с. Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

Однако частенько квадратные уравнения выглядят слегка иначе. Например, вот так:

Это неполные квадратные уравнения. Их тоже можно решать через дискриминант. Надо только правильно сообразить, чему здесь равняются a, b и с.

Сообразили? В первом примере a = 1; b = -4; а c? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с, а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всякого дискриминанта. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х = 0, или х = 4

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем через дискриминант.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х = +3 и х = -3.

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый. Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1, проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком. Если не получилось – значит уже где-то накосячили. Ищите ошибку. Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b, который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в предыдущем разделе. При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно.

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Дробные уравнения. ОДЗ.

Продолжаем осваивать уравнения. Мы уже в курсе, как работать с линейными уравнениями и квадратными. Остался последний вид – дробные уравнения. Или их ещё называют гораздо солиднее – дробные рациональные уравнения. Это одно и то же.

Дробные уравнения.

Как ясно из названия, в этих уравнениях обязательно присутствуют дроби. Но не просто дроби, а дроби, у которых есть неизвестное в знаменателе. Хотя бы в одном. Например:

Напомню, если в знаменателях только числа, это линейные уравнения.

Как решать дробные уравнения? Прежде всего – избавиться от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы знаем, что делать… В некоторых случаях оно может превратиться в тождество, типа 5=5 или неверное выражение, типа 7=2. Но это редко случается. Ниже я про это упомяну.

Но как избавиться от дробей!? Очень просто. Применяя всё те же тождественные преобразования.

Нам надо умножить всё уравнение на одно и то же выражение. Так, чтобы все знаменатели посокращались! Всё сразу станет проще. Поясняю на примере. Пусть нам требуется решить уравнение:

Как учили в младших классах? Переносим все в одну сторону, приводим к общему знаменателю и т.д. Забудьте, как страшный сон! Так нужно делать, когда вы складываете или вычитаете дробные выражения. Или работаете с неравенствами. А в уравнениях мы сразу умножаем обе части на выражение, которое даст нам возможность сократить все знаменатели (т.е., в сущности, на общий знаменатель). И какое же это выражение?

В левой части для сокращения знаменателя требуется умножение на х+2 . А в правой требуется умножение на 2. Значит, уравнение надо умножать на 2(х+2). Умножаем:

Это обычное умножение дробей, но распишу подробно:

Обратите внимание, я пока не раскрываю скобку (х + 2)! Так, целиком, её и пишу:

В левой части сокращается целиком (х+2), а в правой 2. Что и требовалось! После сокращения получаем линейное уравнение:

А это уравнение уже решит всякий! х = 2.

Решим ещё один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2х = 2х/1, можно записать:

И опять избавляемся от того, что нам не очень нравится – от дробей.

Видим, что для сокращения знаменателя с иксом, надо умножить дробь на (х – 2). А единицы нам не помеха. Ну и умножаем. Всю левую часть и всю правую часть:

Опять скобки (х – 2) я не раскрываю. Работаю со скобкой в целом, как будто это одно число! Так надо делать всегда, иначе ничего не сократится.

С чувством глубокого удовлетворения сокращаем (х – 2) и получаем уравнение безо всяких дробей, в линеечку!

А вот теперь уже раскрываем скобки:

Приводим подобные, переносим всё в левую часть и получаем:

Классическое квадратное уравнение. Но минус впереди – нехорош. От него можно всегда избавиться, умножением или делением на -1. Но если присмотреться к примеру, можно заметить, что лучше всего это уравнение разделить на -2! Одним махом и минус исчезнет, и коэффициенты посимпатичнее станут! Делим на -2. В левой части – почленно, а в правой – просто ноль делим на -2, ноль и получим:

Решаем через дискриминант и проверяем по теореме Виета. Получаем х = 1 и х = 3. Два корня.

Как видим, в первом случае уравнение после преобразования стало линейным, а здесь – квадратным. Бывает так, что после избавления от дробей, все иксы сокращаются. Остаётся что-нибудь, типа 5=5. Это означает, что икс может быть любым. Каким бы он не был, всё равно сократится. И получится чистая правда, 5=5. Но, после избавления от дробей, может получиться и совсем неправда, типа 2=7. А это означает, что решений нет! При любом иксе получается неправда.

Осознали главный способ решения дробных уравнений? Он прост и логичен. Мы меняем исходное выражение так, чтобы исчезло всё то, что нам не нравится. Или мешает. В данном случае это – дроби. Точно так же мы будем поступать и со всякими сложными примерами с логарифмами, синусами и прочими ужасами. Мы всегда будем от всего этого избавляться.

Однако менять исходное выражение в нужную нам сторону надо по правилам, да… Освоение которых и есть подготовка к ЕГЭ по математике. Вот и осваиваем.

Сейчас мы с вами научимся обходить одну из главных засад на ЕГЭ! Но для начала посмотрим, попадаете вы в неё, или нет?

Разберём простой пример:

Дело уже знакомое, умножаем обе части на (х – 2), получаем:

Напоминаю, со скобками (х – 2) работаем как с одним, цельным выражением!

Здесь я уже не писал единичку в знаменателях, несолидно… И скобки в знаменателях рисовать не стал, там кроме х – 2 ничего нет, можно и не рисовать. Сокращаем:

Раскрываем скобки, переносим всё влево, приводим подобные:

Решаем, проверяем, получаем два корня. х = 2 и х = 3. Отлично.

Предположим в задании сказано записать корень, или их сумму, если корней больше одного. Что писать будем?

Если решите, что ответ 5, – вы попали в засаду. И задание вам не засчитают. Зря трудились… Правильный ответ 3.

В чём дело?! А вы попробуйте проверку сделать. Подставить значения неизвестного в исходный пример. И если при х = 3 у нас всё чудненько срастётся, получим 9 = 9, то при х = 2 получится деление на ноль! Чего делать нельзя категорически. Значит х = 2 решением не является, и в ответе никак не учитывается. Это так называемый посторонний или лишний корень. Мы его просто отбрасываем. Окончательный корень один. х = 3.

Как так?! – слышу возмущённые возгласы. Нас учили, что уравнение можно умножать на выражение! Это тождественное преобразование!

Да, тождественное. При маленьком условии – выражение, на которое умножаем (делим) – отлично от нуля. А х – 2 при х = 2 равно нулю! Так что всё честно.

И что теперь делать?! Не умножать на выражение? Каждый раз проверку делать? Опять непонятно!

Спокойно! Без паники!

В этой тяжелой ситуации нас спасут три магических буквы. Я знаю, о чем вы подумали. Правильно! Это ОДЗ. Область Допустимых Значений.

Содержание

Решение дробных уравнений с преобразованием в квадратные уравнения
Решение уравнений с дробями
Понятие дроби
Основные свойства дробей
Понятие уравнения
Понятие дробного уравнения
Как решать уравнения с дробями
1. Метод пропорции
2. Метод избавления от дробей
Что еще важно учитывать при решении
Универсальный алгоритм решения
Примеры решения дробных уравнений
🎬 Видео

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Решение дробных уравнений с преобразованием в квадратные уравнения

Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение .

Решать дробные уравнения удобно в следующем порядке:

найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
решить получившееся целое уравнение,
исключить из его корней те, которые обращают в нуль общий знаменатель.

Пример 1. Решить дробное уравнение:

Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:

Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.

Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение

Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение

Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.

Пример 2. Решить дробное уравнение:

Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —

Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:

Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению

Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:

то же самое, если x = 3 .

Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.

Пример 3. Решить дробное уравнение:

Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:

Общий знаменатель — выражение

Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:

Выполнив преобразования, придём к квадратному уравнению

Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.

Пример 4. Решить дробное уравнение:

Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y :

Корни этого уравнения:

или .

Из уравнения находим, что

Итак, данное уравнение имеет четыре корня:

, .

Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:Дробно рациональное уравнение. ОГЭ математика задача 4 (тип 4) 🔴Скачать

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = −b : а; если а равно нулю, а b не равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = −b : а;
если а равно нулю, а b не равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Квадратное уравнение выглядит так:

ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Видео:ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка;
умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение;
делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2.
Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
Избавимся от знаменателя. Умножим каждый член уравнения на х.