Как решать биквадратное уравнение без замены

Биквадратное уравнение — уравнение, которое можно привести к виду:

Для решения биквадратных уравнений x 2 заменяется на любую другую букву, например, на y, то есть:

Следовательно, относительно y, уравнение является квадратным и решается по формуле корней квадратного уравнения, а затем вычисляются корни биквадратного уравнения, если они есть.

Пример. Решить уравнение:

Решение: Заменяем x 2 на y, чтобы получить квадратное уравнение:

D = b 2 — 4ac = (-10) 2 — 4 · 1 · 9 = 100 — 36 = 64, D > 0.

Видео:Биквадратные уравнения. 8 класс алгебра.Скачать

Биквадратные уравнения: решение уравнений, примеры

Содержание:

В самом начале напомним, что в математике принято называть уравнением. Уравнение представляет собой равенство, содержащее одну или более неизвестных величин. Решить уравнение означает найти значение неизвестной величины (или нескольких неизвестных) таким образом, чтобы их подстановка в исходное выражение давала истинное математическое равенство.

Далее подробно расскажем о биквадратных уравнениях и способах их решения. Небольшой урок по этой теме – основа, которая может оказаться неплохим подспорьем, в тот момент, когда настанет время сдавать тест по алгебре. Таким образом не приходя в школьный класс, вы сможете вполне уверенно находить решение любого биквадратного уравнения.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Формула биквадратного уравнения

ax 4 +bx 2 +c = 0, где

a и b – числовые коэффициенты,

с – свободный член.

При этом коэффициент «a» не должен равняться нулю.

Видео:5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать

Решение биквадратных уравнений

Для полной ясности рассмотрим, как решается биквадратное уравнение на примерах.

Видео:Биквадратное уравнениеСкачать

Биквадратные уравнения: примеры для решения

Сначала выполним замену переменной x2 = t и запишем новое квадратное уравнение:

Находим дискриминант для квадратного уравнения по известной формуле:

D = b 2 – 4ac = (-5) 2 – 4 ∙ 1 ∙ 4 = 9.

Напомним о том, что в случае, когда дискриминант оказывается меньше нуля, то уравнение не будет иметь корней, а когда он равен нулю, то корень будет один.

Так как полученный дискриминант D>0, то уравнение будет иметь два корня, которые найдем по формулам: t₁ = -b+D2a и -b-D2a.

Теперь задача состоит в подстановке найденных корней в формулу, по которой мы ранее изменили переменную:

x 2 = 1 и x 2 = 4.

Корни этих уравнений очевидны, но все-таки найдем их традиционным для математики способом. Для этого занесем обе части полученных равенств под знак квадратного корня:

x 2 = 1, тогда x₁ = 1 и x₂ = –1.

x 2 = 4, тогда x₃ = 2 и x₄ = –2.

Ответ. Таким образом мы получили четыре искомых корня биквадратного уравнения

Теперь рассмотрим другой пример, в котором корни биквадратного уравнения будем находить без вычисления дискриминанта. Задание будет состоять в решении уравнения:

В этом случае будет вполне логично вынести переменную x 2 за скобки, тогда получим выражение: x 2 (–9x 2 +81) = 0.

Теперь можно приравнять к нулю каждый из сомножителей уравнения.

x 2 = 0, соответственно один из корней нашего уравнения x₁ = 0.

Второе равенство решаем следующим путем:

Заносим под знак радикала обе части полученного равенства

x 2 = 9, тогда x₂ = 3 и x₃ = –3.

Ответ. Получено три корня заданного биквадратного уравнения: x₁ = 0, x₂ = 3 и x₃ = –3.

Таким образом на примерах из школьной программы мы продемонстрировали как решать биквадратные уравнения различными способами. Надеемся, что приведенная информация будет полезной при сдаче теста.

Видео:МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать

Биквадратное уравнение. Алгоритм решения и примеры.

Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.

Видео:Уравнения, сводящиеся к квадратным. Биквадратное уравнениеСкачать

Формула биквадратного уравнения:

Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.

ax 4 +bx 2 +c=0, где a≠0

Видео:Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать

Как решаются биквадратные уравнения?

Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю

Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.

(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:

Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.

Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)

Возвращаемся в замену, подставим вместо переменной t полученное число:

Можно не во всех случаях делать замену. Рассмотрим пример.

Пример №3:
Решить биквадратное уравнение.

Выносим переменную x 2 за скобку,

Приравниваем каждый множитель к нулю

Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)

Пример №4:
Решите биквадратное уравнение.
(x^-16=0)

Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)

Ответ: решения нет.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

🔍 Видео

Решение биквадратных уравнений. Практическая часть. 1ч. 8 класс.Скачать

Урок 1. №20 ОГЭ. Биквадратные уравнения. Как делать замену, чтобы не запутаться?Скачать

ЗАДАНИЕ 18 ПАРАМЕТРЫ ЕГЭ ПРОФИЛЬ ПУТЬ К 90+ БАЛЛАМ С НУЛЯ 2024[6]| ЧАСТЬ - 19Скачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

ОГЭ 2019 ЗАДАНИЕ 21. Биквадратное уравнение.Скачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

БИКВАДРАТНОЕ УРАВНЕНИЕ класс математикаСкачать

Биквадратное уравнениеСкачать

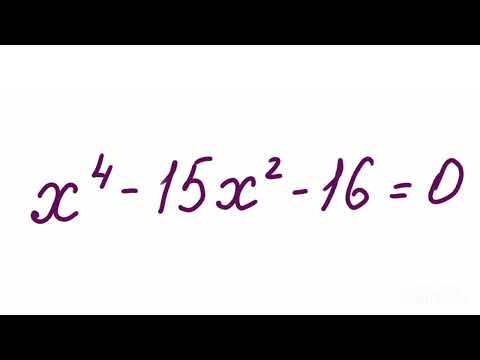
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Биквадратное уравнениеСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать