Как расположены между собой сфера заданная уравнением и плоскость заданная уравнением

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Мы продолжаем знакомство со сферой.

На прошлом занятии вы узнали, что в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Рассмотрим взаимное расположение плоскости и сферы в зависимости от соотношения между расстоянием от её центра до плоскости и радиусом сферы.

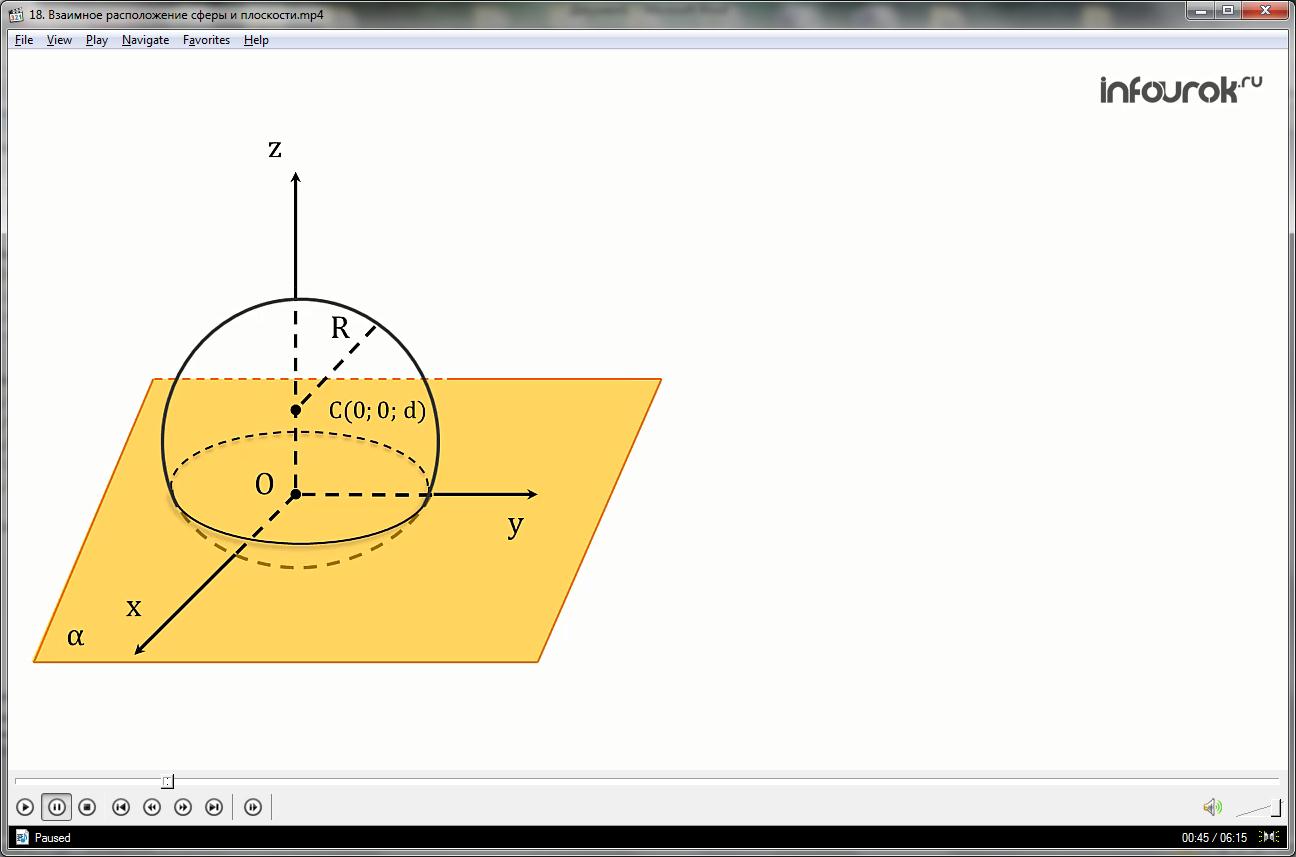
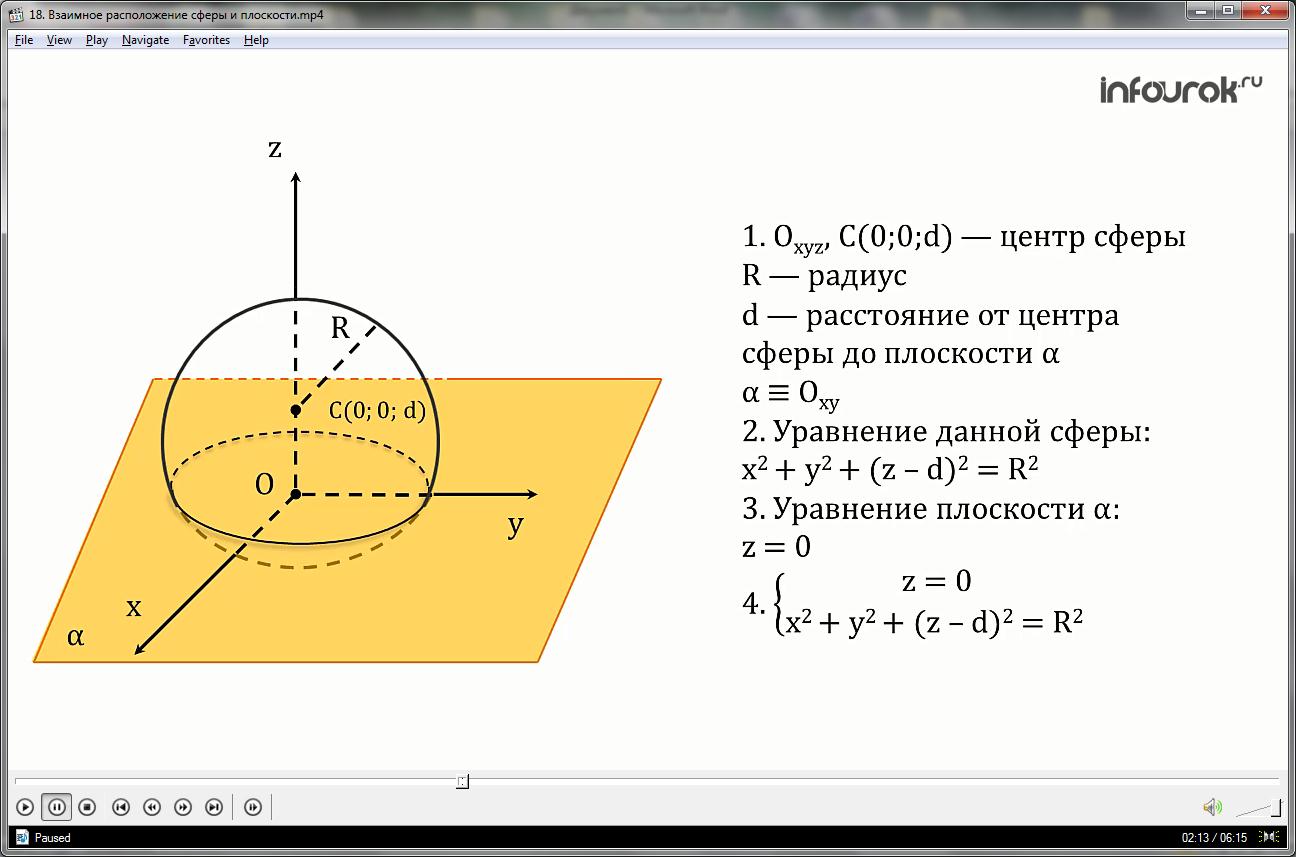
1.Выберем прямоугольную систему координат Оxyz так, что центр сферы радиуса R имеет координаты С (0;0;d), где d-расстояние от центра сферы до данной плоскости α, а сама плоскость α совпадает с координатной плоскостью Оxy.

2.Запишем уравнение данной сферы:

3.Очевидно, что аппликата z любой точки плоскости Оxy равна нулю, то есть координаты любой точки плоскости Оxy удовлетворяют уравнению z=0, а координаты любой точки, не принадлежащей плоскости Оxy, этому уравнению не удовлетворяют, так как аппликаты таких точек не равны нулю.

Тем самым в соответствии с понятием уравнения поверхности, уравнение z=0 является уравнением координатной плоскости Оxy, таким образом, уравнение плоскости α имеет вид:

4.Взаимное расположение сферы и плоскости зависит от решения системы уравнений:

При z=0 второе уравнение примет вид:

Рассмотрим возможные три случая:

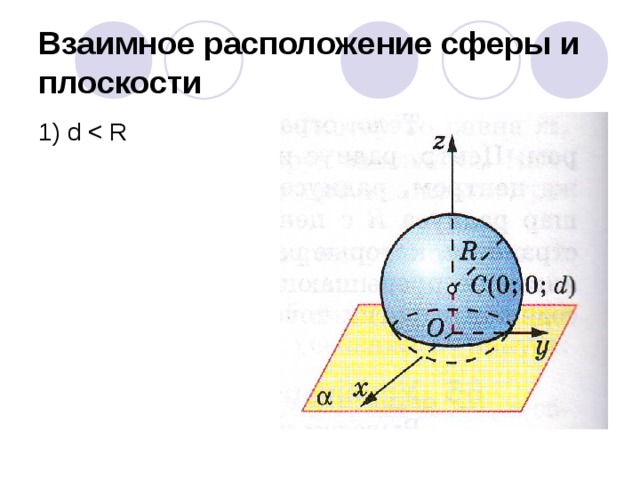
1) Расстояние от центра сферы до плоскости меньше радиуса сферы

d R. Тогда R2- d2 0 и уравнение x2+y2 = R2- d2 является уравнением окружности радиуса

r=√ R2- d2 , все точки этой окружности принадлежат одновременно и сфере и плоскости.

Итак, плоскость и сфера пересекаются по окружности.

Таким образом, если расстояние от центра до плоскости меньше радиуса сферы, то сечение сферы данной плоскостью является окружностью.

Очевидно, что сечение шара плоскостью является кругом, причем:

если секущая плоскость проходит через центр шара, то в сечении получается круг, радиус которого равен радиусу шара;

если секущая плоскость не проходит через центр, то в сечении получается круг, радиус которого меньше радиуса шара.

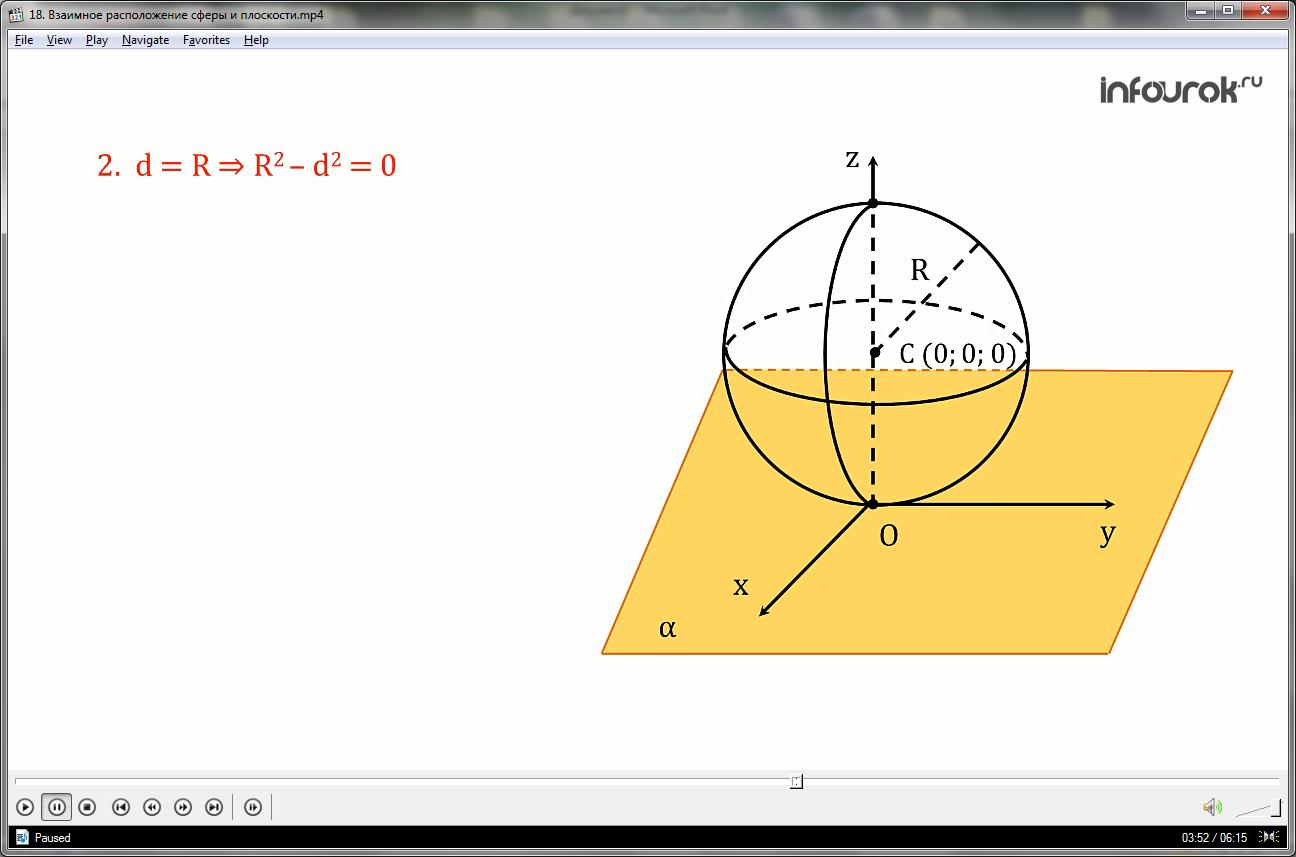
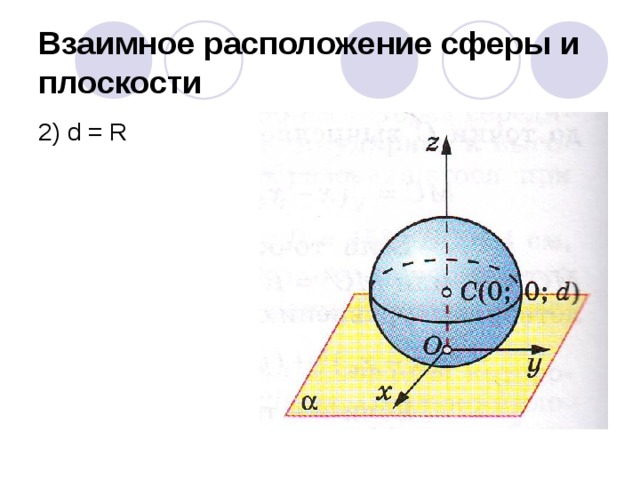
2). Расстояние от центра сферы до плоскости равно радиусу сферы

d=R, тогда R2- d2=0 и уравнению

x2+y2 = R2- d2 удовлетворяют только значения

x=0, y=0. Поэтому только координаты точки О (0;0;0) удовлетворяют обоим уравнениям, итак точка О — единственная общая точка плоскости и сферы.

Таким образом, если расстояние до плоскости равно радиусу сферы, то плоскость и сфера имеют единственную общую точку.

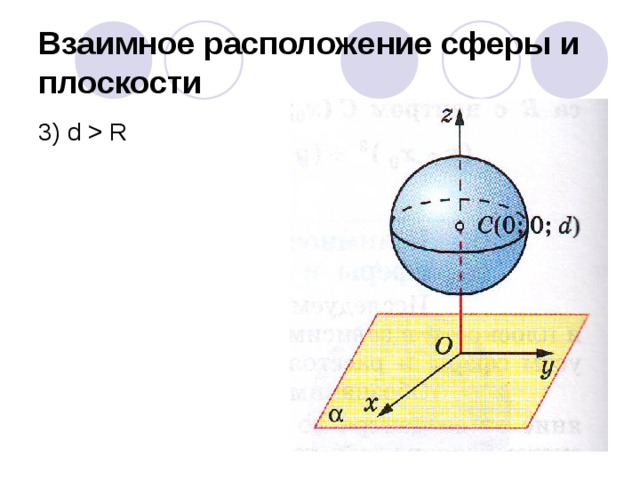
3) Расстояние от центра сферы до плоскости больше радиуса сферы

d R, в этом случае R2- d2 0 и уравнение

x2+y2 = R2- d2 не имеет решения.

Таким образом, если расстояние от центра сферы до плоскости больше радиуса сферы, то плоскость и сфера не имеют общих точек.

Применим полученные знания при решении задач.

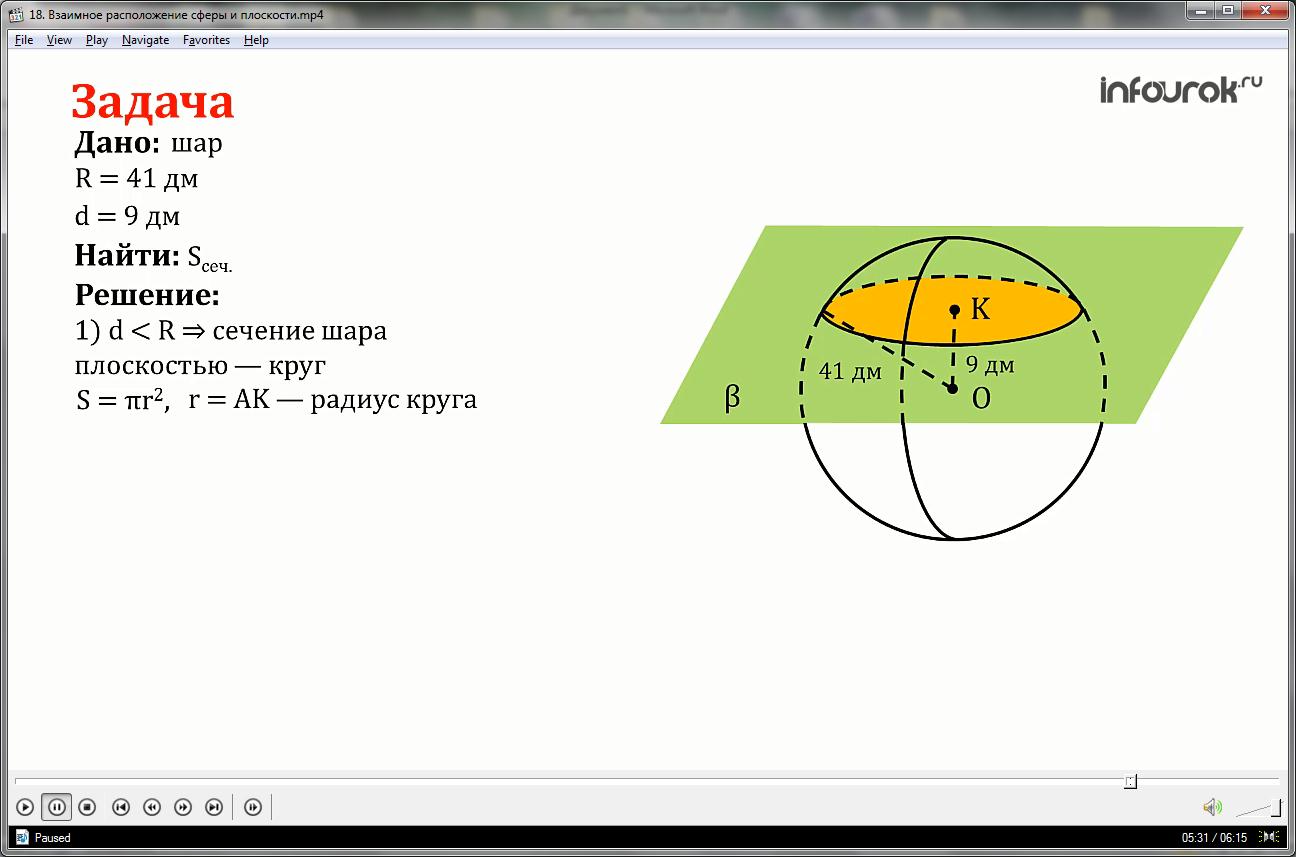
Шар с радиусом 41 дм пересечён плоскостью, проходящей на расстоянии 9 дм от центра. Найти площадь сечения.

1.Расстояние от центра шара до секущей плоскости меньше радиуса, значит сечением шара плоскостью, является круг.

Площадь круга вычислим по формуле:

S=πr2, где r = АК — радиус круга.

2.Найдём АК из прямоугольного треугольника

АОК по теореме Пифагора:

3. Sсеч= r2= *402=1600 (дм2).

Таким образом, площадь сечения равна 1600 дм2.

Сегодня мы рассмотрели возможные случаи взаимного расположения сферы и плоскости, применили свои знания при решении задач.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Презентация по геометрии «Взаимное расположение сферы и плоскости»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Взаимное расположение сферы и плоскости

Устный опрос: Определение сферы? Определение шара? Общий вид уравнения сферы? Являются ли заданные уравнения уравнениями сферы? Если да, найдите координаты центра сферы и радиус сферы.

Математический диктант Вариант 1Вариант 2 1. Найдите координаты центра и радиус сферы, заданной уравнением1. Найдите координаты центра и радиус сферы, заданной уравнением 2. Напишите уравнение сферы радиуса R с центром в точке А, если А (2; 0; –1), R=72. Напишите уравнение сферы радиуса R с центром в точке А, если А (–2; 1; 0), R=6 3. Проверьте, лежит ли точка А на сфере, заданной уравнением, если А(–2; 1; 4)3. Проверьте, лежит ли точка А на сфере, заданной уравнением, если А(5; –1; 4) 4. Докажите, что данное уравнение является уравнением сферы: 4. Докажите, что данное уравнение является уравнением сферы:

Возможны три случая взаимного расположения сферы и плоскости: 1) В данном случае сфера и плоскость пересекаются по окружности. Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность. Пусть R – радиус сферы, d – расстояние от сферы до плоскости α

2) Уравнение сферы и плоскость имеют единственную общую точку. Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.

3) Уравнение сферы и плоскость не имеют общих точек. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Задание на дом п.66, повторить п. 64, 65 №№ 579 (в, г), 582

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 710 человек из 76 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 859 человек из 77 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 48 человек из 21 региона

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 848 860 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 14.04.2016
• 1484
• 8

• 14.04.2016
• 5438
• 9

• 14.04.2016
• 2699
• 5

• 14.04.2016
• 1251
• 0

• 14.04.2016
• 3085
• 37

• 14.04.2016
• 1110
• 23

• 14.04.2016
• 1682
• 16

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 14.04.2016 2161
• PPTX 217.5 кбайт
• 64 скачивания
• Рейтинг: 1 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Гайдарова Хадижат Гайдаровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 7 месяцев
• Подписчики: 0
• Всего просмотров: 9220
• Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:11 класс, 21 урок, Взаимное расположение сферы и плоскостиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения предлагает изменить форму для проведения ВОШ

Время чтения: 1 минута

В России выросло число детей с ОВЗ, поступающих в колледжи

Время чтения: 1 минута

В каждом округе Москвы появятся школьные службы примирения

Время чтения: 3 минуты

25% школ выбрали компьютерный формат проведения ВПР

Время чтения: 1 минута

В Госдуму внесли законопроект о возможности повторной сдачи ЕГЭ

Время чтения: 1 минута

Минобрнауки РФ откроет центр по сбору учебников для школьников и студентов из ЛНР и ДНР

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости

Урок геометрии в 11 классе

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости

Просмотр содержимого документа
«Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости»

Сфера. Уравнение сферы. Взаимное расположение сферы и плоскости.

• Окружность – множество точек плоскости, равноудаленных от данной точки
• Точка О – центр окружности
• ОА — радиус

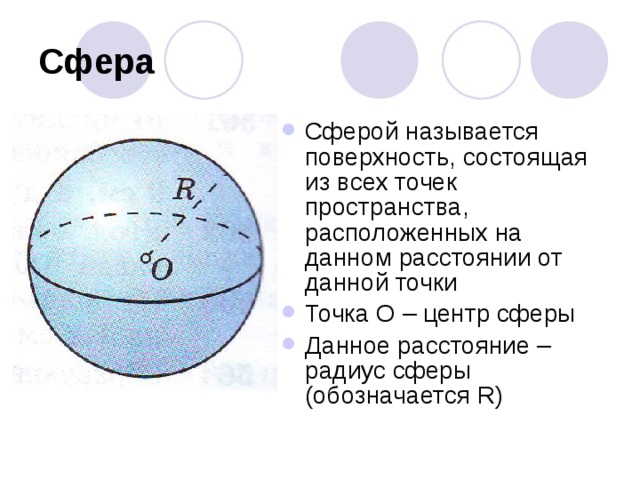
• Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки
• Точка О – центр сферы
• Данное расстояние – радиус сферы (обозначается R)

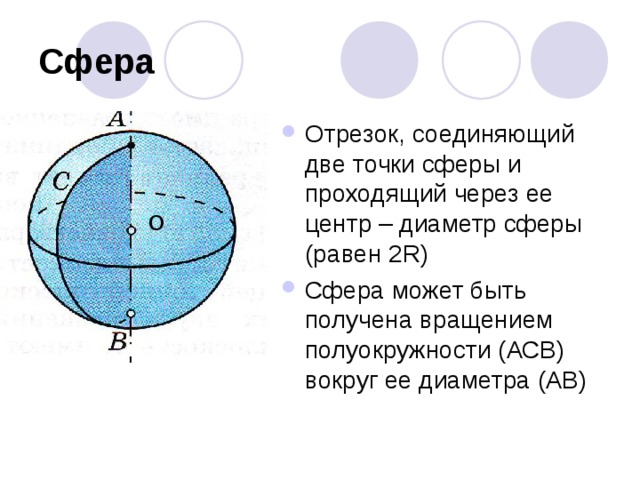
• Отрезок, соединяющий две точки сферы и проходящий через ее центр – диаметр сферы (равен 2 R )
• Сфера может быть получена вращением полуокружности (АСВ) вокруг ее диаметра (АВ)

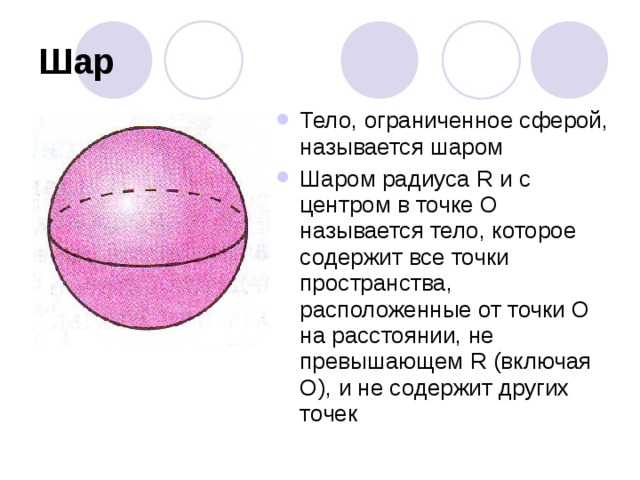
• Тело, ограниченное сферой, называется шаром
• Шаром радиуса R и с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек

• Пусть R – радиус сферы
• С(х˳,у˳, z ˳) – центр окружности
• Расстояние от произвольной

точки М(х,у, z ) до точки С найдем

Если точка М лежит на данной сфере,

Координаты точки М удовлетворяют

• № 574(а)
• № 576 (а)
• № 577 (а)
• № 578 (устно)

Взаимное расположение сферы и плоскости

• R – радиус сферы
• d – расстояние от центра до плоскости α
• Плоскость Оху совпадает с плоскостью α , поэтому ее уравнение имеет вид z=0
• Центр сферы С лежит на положительной полуоси О z , т.е. имеет координаты С(0;0; d)
• Уравнение сферы

Взаимное расположение сферы и плоскости

Если координаты произвольной точки М (х;у; z) удовлетворяют обоим уравнениям, то М лежит как в плоскости α , так и на сфере.

Вопрос о взаимном расположении сводится к исследованию системы уравнений

Подставив z = 0 во второе уравнение, получим

Взаимное расположение сферы и плоскости

1) d

Взаимное расположение сферы и плоскости

R » width=»640″

Взаимное расположение сферы и плоскости

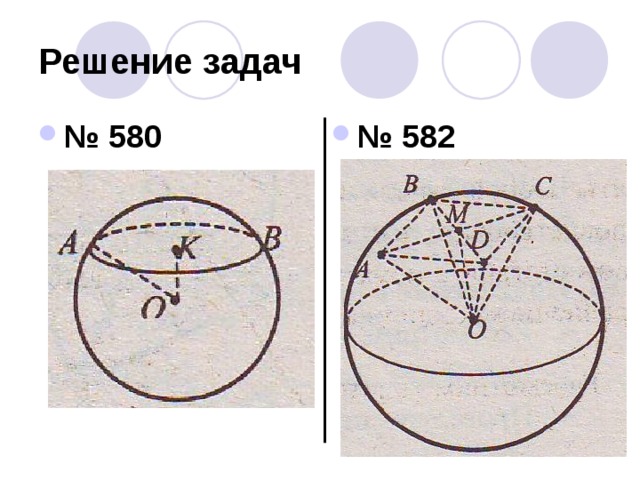
• №580

• №582

📽️ Видео

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

11 класс, 20 урок, Уравнение сферыСкачать

11 класс, 24 урок, Взаимное расположение сферы и прямойСкачать

11 класс, 19 урок, Сфера и шарСкачать

11 класс, 22 урок, Касательная плоскость к сфереСкачать

Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Шар и сфера Взаимное расположение сферы и плоскости Касательная плоскость к сфереСкачать

11. Прямая в пространстве и ее уравненияСкачать

Уравнение прямой, сферы и плоскостиСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

№579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координатыСкачать

11 класс, 23 урок, Площадь сферыСкачать