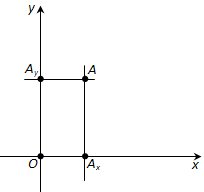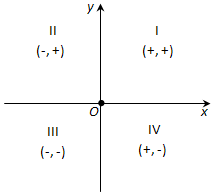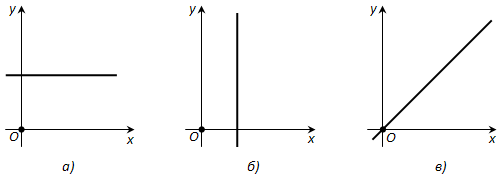Вопрос 1. Объясните, как определяются координаты точки.
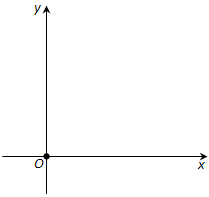
Ответ. Проведём на плоскости через точку O две взаимно перпендикулярные прямые x и y – оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось y – осью ординат. Точкой пересечения O – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая её стрелкой, а другую – отрицательной.
Каждой точке A плоскости мы сопоставим пару чисел – координаты точки – абсциссу (x) и ординату (y) по такому правилу.
Через точку A проведём прямую, параллельную оси ординат (рис. 171). Она пересечёт ось абсцисс x в некоторой точке Ax. Абсциссой точки A мы будем называть число x, абсолютная величина которого равна расстоянию от точки O до точки Ax. Это число будет положительным, если Ax принадлежит положительной полуоси и отрицательным, если Axпринадлежит отрицательной полуоси. Если точка A лежит на оси ординат y, то полагаем x равным нулю.
Ордината (y) точки A определяется аналогично. Через точку A проведём прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечёт ось ординат y в некоторой точке Ay. Ординатой точки A мы будем называть число y, абсолютная величина которого равна расстоянию от точки O до точки Ay. Это число будет положительным, если Ay принадлежит положительной полуоси и отрицательным, если Ay принадлежит отрицательной полуоси. Если точка A лежит на оси абсцисс x, то полагаем y равным нулю.
Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: A (x; y) (на первом месте абсцисса, на втором – ордината).
Вопрос 2. Какие знаки у координат точки, если она принадлежит первой (второй, третьей, четвёртой) четверти?
Ответ. Оси координат разбивают плоскость на четыре части – четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения.
Если точка принадлежит первой четверти, то её абсцисса и ордината будут положительными.
Если точка принадлежит второй четверти, то её абсцисса будет отрицательной, а ордината будет положительной.
Если точка принадлежит третьей четверти, то её абсцисса и ордината будут отрицательными.
Если точка принадлежит четвёртой четверти, то её абсцисса будет положительной, а ордината будет отрицательной.
Вопрос 3. Чему равны абсциссы точек, лежащих на оси ординат?
Чему равны ординаты точек, лежащих на оси абсцисс?
Чему равны координаты начала координат?
Ответ. Точки оси x (оси абсцисс) имеют равные нулю ординаты (y = 0), а точки оси y (оси ординат) имеют равные нулю абсциссы (x = 0).
Если какая-либо точка лежит на оси ординат y, то абсцисса данной точки равна нулю.
Если какая-либо точка лежит на оси абсцисс x, то ордината данной точки равна нулю.
У начала координат абсцисса и ордината равны нулю.
Вопрос 4. Выведите формулы для координат середины отрезка.
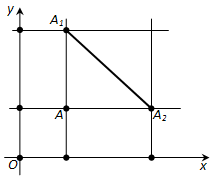
Ответ. Пусть A (x1; y1) и B (x2;y2) – две произвольные точки и C (x; y) – середина отрезка AB. Найдём координаты x, y точки C.
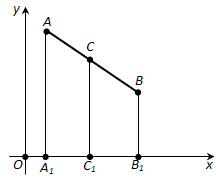
Рассмотрим сначала случай, когда отрезок AB не параллелен оси y, т.е. (x_1 neq x_2). Проведём через точки A, B, C прямые, параллельные оси y (рис. 173). Они пересекут ось x в точках A1 ((x_1); 0), B1 ((x_2); 0), C ((x); 0). По теореме Фалеса точка (C_1) будет серединой отрезка (A_1B_1).
Так как точка (C_1) – середина отрезка (A_1B_1), то (A_1C_1 = B_1C_1), а значит, (|x – x_1| = |x – x_2|). Отсюда следует, что либо (x – x_1 = -(x – x_2)). Первое равенство невозможно, так как (x_1 neq x_2). Поэтому верно второе. А из него получается формула
Если (x_1 = x_2), т.е. отрезок AB параллелен оси y, то все три точки (A_1, B_1, C_1) имеют одну и ту же абсциссу. Значит, формула остаётся верной и в этом случае.
Ордината точки C находится аналогично. Через точки A, B, C проводятся прямые, параллельные оси x. Получается формула
Вопрос 5. Выведите формулу для расстояния между точками.
Ответ. Пусть на плоскости xy даны две точки: (A_1) с координатами (x_1, y_1) и (A_2) с координатами (x_2, y_2). Выразим расстояние между точками (A_2) и (A_2) через координаты этих точек.
Рассмотрим сначала случай, когда (x_1 neq x_2) и (y_1 neq y_2). Проведём через точки (A_1) и (A_2) прямые, параллельные осям координат, и обозначим через A точку их пересечения (рис. 174). Расстояние между точками (A) и (A_1) равно (|y_1 – y_2|), а расстояние между точками (A) и (A_2) равно (|x_1 – x_2|). Применяя к прямоугольному треугольнику (AA_1A_2) теорему Пифагора, получим:
(d^2 = (x_1 — x_2)^2+ (y_1 — y_2)^2), (*)
где d –расстояние между точками (A_1) и (A).
Хотя формула (*) для расстояния между точками выведена нами в предположении (x_1 neq x_2), (y_1 neq y_2), она остаётся верной и в других случаях. Действительно, если (x_1 = x_2), (y_1 neq y_2), то d равно (|y_2 — y_2|). Тот же результат даёт и формула (*). Аналогично рассматривается случай, когда (x_1 neq x_2, y_1 = y_2). При (x_1 = x_2, y_1 = y_2) точки (A_1) и (A_2) совпадают и формула (*) даёт d = 0.
Вопрос 6. Что такое уравнение фигуры в декартовых координатах?
Ответ. Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными x и y, которому удовлетворяют координаты любой точки фигуры. И обратно: любые два числа, удовлетворяющие этому уравнению, являются координатами некоторой точки фигуры.
Вопрос 7. Выведите уравнение окружности.
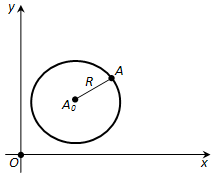
Ответ. Составим уравнение окружности с центром в точке AO (a; b) и радиусом R (рис. 175). Возьмём произвольную точку A (x; y) на окружности. Расстояние от неё до центра AO равен ((x – a)^2 + (y – b)^2). Таким образом, координаты x, y каждой точки A окружности удовлетворяют уравнению
Обратно: любая точка A, координаты которой удовлетворяют уравнению (*), принадлежит окружности, так как расстояние от неё до точки AO равно R. Отсюда следует, что уравнение (*) действительно является уравнением окружности с центром AOи радиусом R. Заметим, что если центром окружности является начало координат, то уравнение окружности имеет вид:
Вопрос 8. Докажите, что прямая в декартовых координатах имеет уравнение вида ax + by + c = 0.
Ответ. Докажем, что любая прямая в декартовых координатах x, y имеет уравнение вида
где a, b, c – некоторые числа.
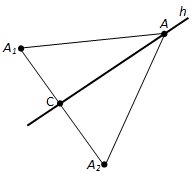
Пусть h – произвольная прямая на плоскости xy. Проведём какую-нибудь прямую, перпендикулярную прямой h, и отложим на ней от точки пересечения C с прямой h равные отрезки CA1 и CA2(рис. 176).
Пусть a1, b1 – координаты точки A1 и a2, b2 – координаты точки A2. Как мы знаем, любая точка A (x; y) прямой h равноудалена от точек A1 и A2. Поэтому координаты её удовлетворяют уравнению
((x – a_1)^2 + (y — b_1)^2 = (x – a_2)^2 + (y — b_2)^2). (**)
Обратно: если координаты x и y какой-нибудь точки удовлетворяют уравнению (**), то эта точка равноудалена от точек A1 и A2, а значит, принадлежит прямой h. Таким образом, уравнение (**) является уравнением прямой h. Если в этом уравнении раскрыть скобки и перенести все члены уравнения в левую его часть, то оно примет вид:
(2(a_2 — a_1)x + 2(b_2 — b_1)y + (a_1^2 + b^2_1 — a^2_2 — b^2_2) = 0.)
Обозначая (2(a_2 — a_1) = a), (2(b_2 — b_1) = b), (a^2_1 + b^2_1 — a^2_2 — b^2_2 = c), получаем уравнение (*). Утверждение доказано.
Вопрос 9. Как найти координаты точки пересечения двух прямых, если заданы уравнения этих прямых?
Ответ. Пусть заданы уравнения двух прямых:
Найдём координаты их точки пересечения.
Так как точка пересечения (x; y) принадлежит каждой из прямых, то её координаты удовлетворяют и первому и второму уравнению. Поэтому координаты точки пересечения являются решением системы уравнений, задающих прямые. Рассмотрим пример.
Пусть уравнениями данных прямых будут:
Решая эту систему уравнений, находим x = -3, y = -7. Точка пересечения прямых (-3; -7).
Вопрос 10. Как расположена прямая, если в её уравнении коэффициент a = 0 (b = 0; c = 0)?
Ответ. Выясним, как расположена прямая относительно осей координат, если её уравнение ax + by + c = 0 имеет тот или иной частный вид.
1. a = 0, b (neq) 0. В этом случае уравнение прямой можно переписать так:
Таким образом, все точки прямой имеют одну и ту же ординату ((-frac)); следовательно, прямая параллельна оси x (рис. 177, а). В частности, если c = 0, то прямая совпадает с осью x.
2. b = 0, a (neq) 0. Этот случай рассматривается аналогично. Прямая параллельна оси y (рис. 177, б) и совпадает с ней, если c = 0.
3. c = 0. Прямая проходит через начало координат, так как его координаты (0; 0) удовлетворяют уравнению прямой (рис. 177, в).
- Общее уравнение прямой на плоскости. Неполные уравнения прямой
- Общее уравнение прямой: описание, примеры, решение задач
- Общее уравнение прямой: основные сведения
- Неполное уравнение общей прямой
- Общее уравнение прямой, проходящей через заданную точку плоскости
- Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
- Составление общего уравнения прямой
- 🎥 Видео
Видео:Угловой коэффициент прямойСкачать

Общее уравнение прямой на плоскости. Неполные уравнения прямой
Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.
Уравнение Ax + By + C = 0 называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.
Если коэффициент B = 0, A ≠ 0 ≠ C , то из уравнения Ax + By + C = 0 следует x = — C / A = a. Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а.
Если коэффициент A = 0, B ≠ 0 ≠ C то из уравнения Ax + By + C = 0 следует y = — C / B = b. Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b.
Если C = 0, то уравнение Ax + By + C = 0 принимает вид Ax + By = 0. Ясно, что эта прямая проходит через начало координат.
Если в уравнении Ax + By = 0 коэффициент B ≠ 0 , то отсюда получаем y = — 
k = — 
Если в уравнении Ax + By = 0 A ≠ B = 0, то Ax = 0 и, сокращая на А, получаем уравнение оси Оу: x = 0.
Если в уравнении Ax + By = 0 B ≠ A = 0, то By = 0 и, сокращая на В, получаем уравнение оси Ох: y = 0.
Подведем итог исследования общего уравнения прямой Ax + By + C = 0:
1) Если A ≠ 0, B ≠ 0, C ≠ 0 , то уравнение Ax + By + C = 0 может быть записано в виде уравнения прямой в отрезках: x /a + y / b = 1 – прямая, отсекающая от осей координат отрезки величиной а и b соответственно.
2) Если A = 0, B ≠ 0, C ≠ 0, то уравнение может быть записано в виде: y = b – прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b.
3) Если A ≠ 0, B = 0, C ≠ 0, то уравнение может быть записано в виде: x = a – прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а.
4) Если A = 0, B ≠ 0, C = 0, то уравнение прямой имеет вид: y = 0 – прямая совпадает с осью Ох.
5) Если A ≠ 0, B = 0, C = 0, то уравнение прямой имеет вид: x = 0 – прямая совпадает с осью Оу.
6) Если A ≠ 0, B ≠ 0, C = 0, то уравнение может быть записано в виде: y = k * x – уравнение прямой с угловым коэффициентом.
17. Общее уравнение прямой на плоскости. Уравнение прямой в «отрезках» (с выводом)
Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.
Уравнение прямой в отрезках: 

Пусть ни один из коэффициентов А, В, С общего уравнения прямой Ax + By + C = 0, не равен нулю. Перенесем свободный член С в правую часть уравнения и разделим обе части уравнения на (– С):
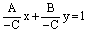
Обозначим 


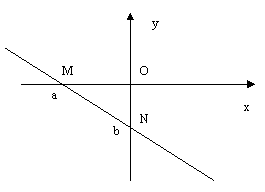
Для построения прямой достаточно взять две точки на этой прямой. Для построения прямой в отрезках удобно найти ее точки пересечения с координатными осями:
М(а, 0) – точка пересечения прямой : 

N(0, b) – точка пересечения прямой : 

Говорят, что прямая отсекает от координатных осей отрезки ОМ и ОN величина которых равна числам а и b соответственно. Под величиной отрезка ОА здесь понимается не его длина 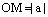
Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Видео:Занятие 1. График линейной функции y=kx+bСкачать

Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
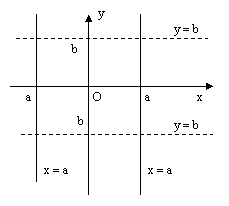
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Видео:Угловой коэффициент прямой. Решение задач.Скачать

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Видео:Составляем уравнение прямой по точкамСкачать

Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
🎥 Видео
Вариант 51, № 7. Нахождение k и b линейной функции y=kx+b. Пример 1Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Коэффициент угла наклона прямойСкачать
№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Уравнение прямой ax плюс by плюс c равно 0. Доказательство теоремы. Урок 1. Геометрия 8 класс.Скачать

Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

[ОГЭ] На рисунках изображены графики функций вида у = кх + ЬСкачать
![[ОГЭ] На рисунках изображены графики функций вида у = кх + Ь](https://i.ytimg.com/vi/YiHEVLltWDk/0.jpg)
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать