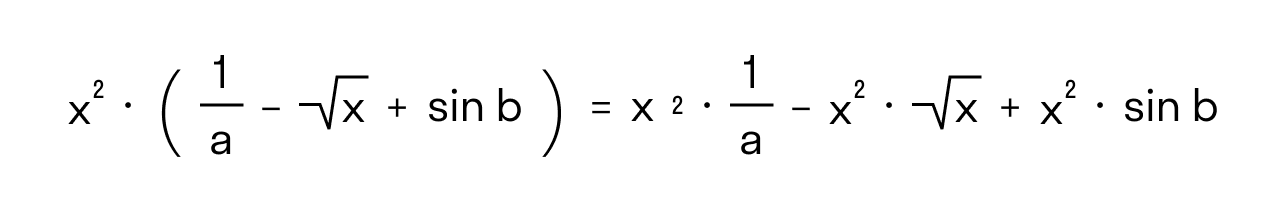О чем эта статья:
- Понятие раскрытия скобок
- Первое правило раскрытия скобок
- Второе правило раскрытия скобок
- Другие правила раскрытия скобок
- Таблица с формулами раскрытия скобок
- Скобка в скобке
- Порядок раскрытия скобок
- Задачи для самостоятельного решения
- Раскрытие скобок: правила и примеры (7 класс)
- Правила раскрытия скобок
- Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря:
- Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:
- Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть:
- При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
- Скобка в скобке
- Раскрытие скобок: правила, примеры, решения
- Что называется раскрытием скобок?
- Правила раскрытия скобок, примеры
- У одиночных чисел в скобках
- В произведениях двух чисел
- В произведениях трех и большего количества чисел
- Раскрытие скобок, перед которыми стоит знак «+»
- Как раскрываются скобки, перед которыми стоит знак минус
- Раскрытие скобок при умножении числа на скобку, выражения на скобку
- Умножение скобки на скобку
- Раскрытие скобок в произведениях нескольких скобок и выражений
- Скобка в натуральной степени
- Деление скобки на число и скобки на скобку
- Порядок раскрытия скобок
- 🎦 Видео
Видео:Раскрытие скобок. 6 класс.Скачать

Понятие раскрытия скобок
В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.
Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.
Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:
Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.
Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.
В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:
- знаки плюс или минус перед скобками, которые заключают сумму или разность, например, (a + 7) и -(-3 + 2a — 12 — b);
- произведение числа, одной или нескольких букв и суммы или разности в скобках, например, 3(2 — 7), (3 — a + 8c)(-b) или -2a(b + 2c — 3m).
Раскрытие скобок также можно рассматривать шире.
Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:
Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:
Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.
Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:
- 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1
Видео:КАК РАСКРЫТЬ СКОБКИ?Скачать

Первое правило раскрытия скобок
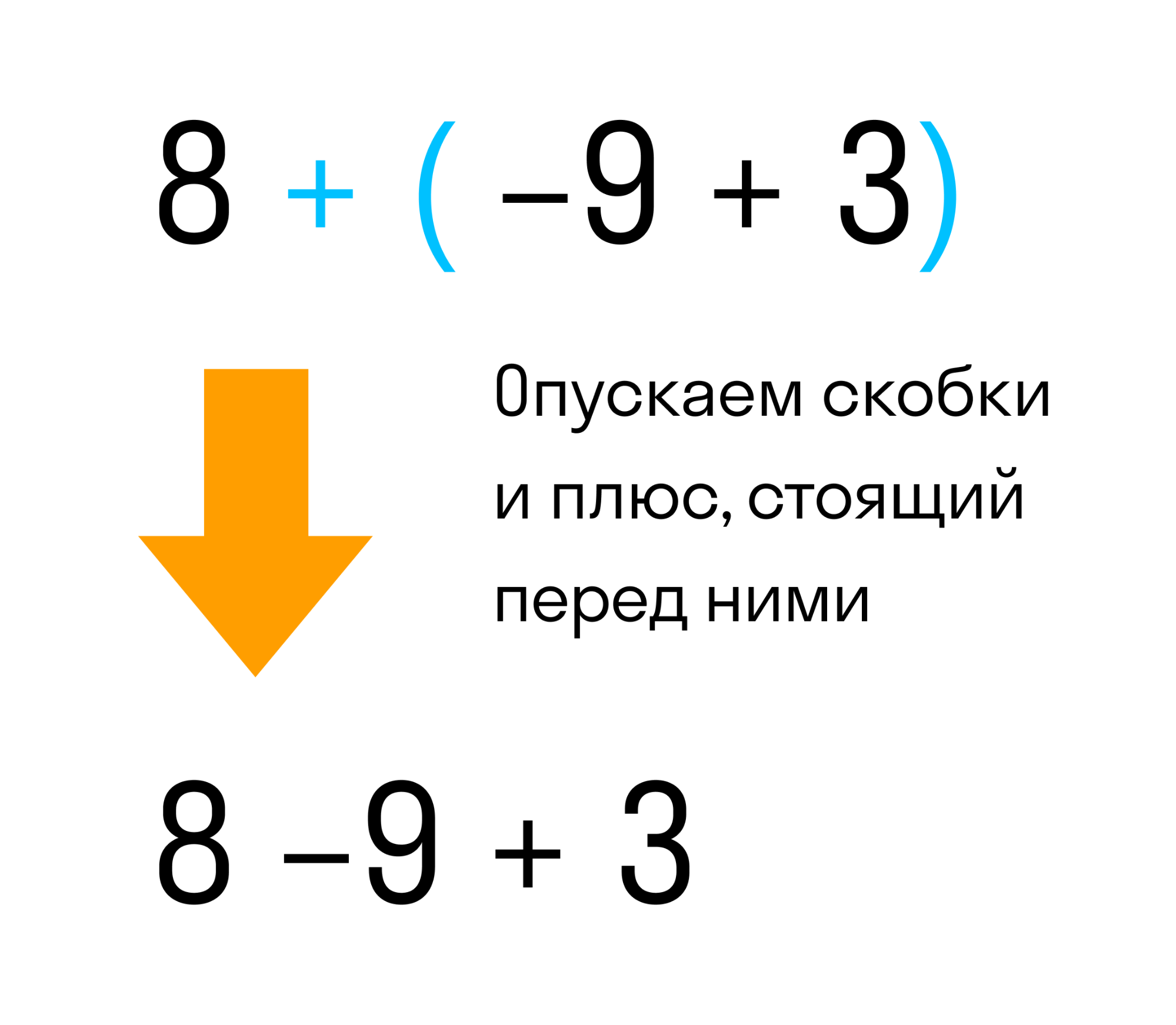
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.
Первое правило раскрытия скобок
Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.
Формула раскрытия скобок
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.
Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
Потренируемся применять правило на примерах.
Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)
Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:
Пример 2. Раскрыть скобки в выражении 6 + (−2)
Перед скобками стоит плюс, значит применим то же правило:
Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.
В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.
Идем дальше. Теперь упростим выражение 2a + a − 5b + b.
Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
- 2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)
Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.
Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.
После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:
Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:
- 2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3. Раскрыть скобки 6 + (−3) + (−2)
В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:
Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.
Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
- 1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4. Раскрыть скобки в выражении (−7)
Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:
Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)
Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Ставим правильно знаки при раскрытии скобок.Скачать

Второе правило раскрытия скобок
Здесь рассмотрим второе правило раскрытия скобок. Звучит так:
Второе правило раскрытия скобок
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.
Формула раскрытия скобок
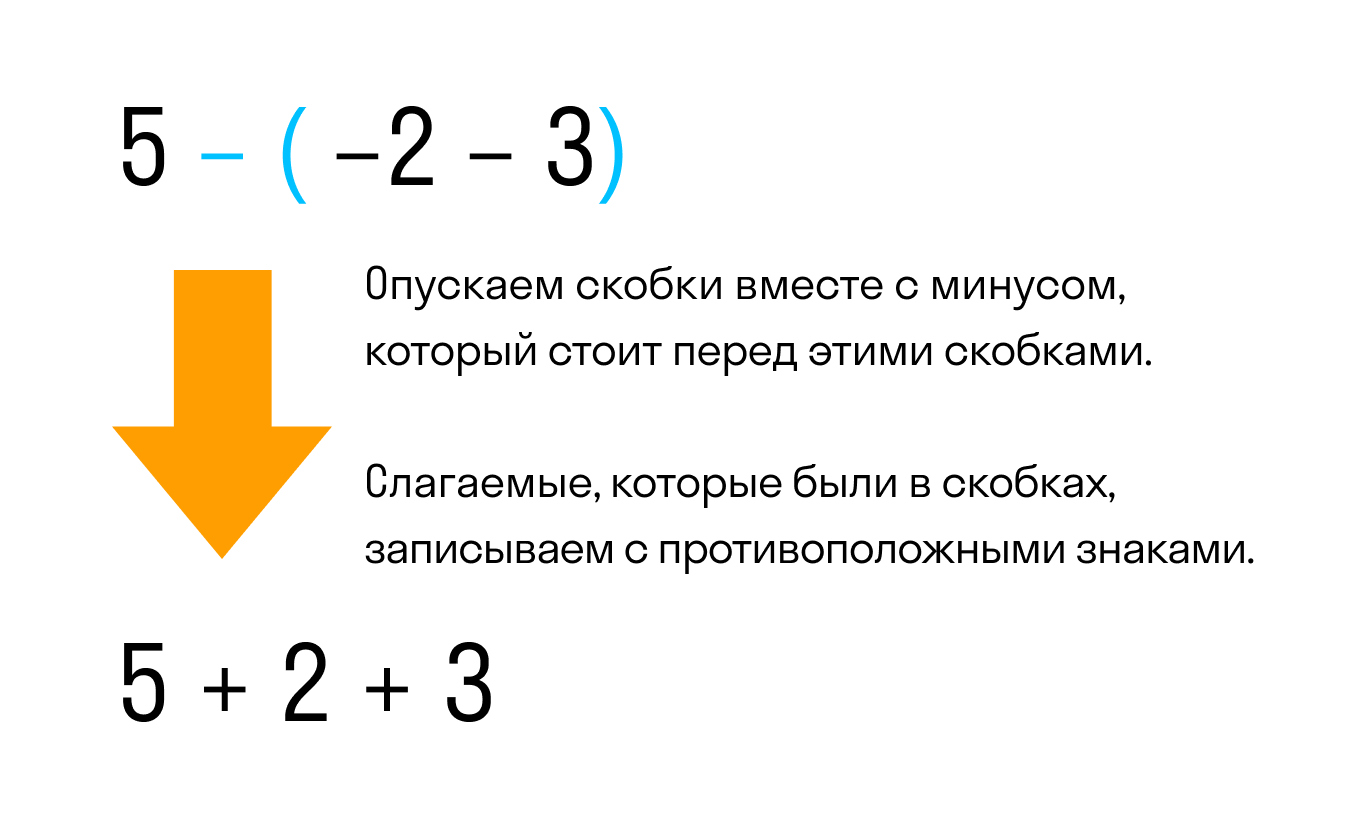
Например, раскроем скобки в выражении 5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:
Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.
Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:
Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
18 − (−1 − 5) = 18 + 1 + 5
Пример 2. Раскрыть скобки −(−6 + 7)
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)
Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:
−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2
Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
a − (3b + 3) + 10 = a − 3b − 3 + 10
Видео:Видеоурок по теме РАСКРЫТИЕ СКОБОКСкачать

Другие правила раскрытия скобок
Правило раскрытия скобок при делении
Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.
Формула раскрытия скобок
(a + b) : c = a/c + b/c.
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:
Далее умножим скобку на число:
- (x + 2) * 3/2 = x * 3/2 + 2 * 3/2.
| (=7x+2(5) (-3x-y) ()=) Теперь раскрываем вторую скобку, внешнюю. Упрощаем получившееся выражение… Пример. Раскройте скобки и приведите подобные слагаемые (-(x+3(2x-1+(x-5)))). Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается. Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке. Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него. И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные. Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме. Видео:КАК РАСКРЫТЬ СКОБКИ И УПРОСТИТЬ ВЫРАЖЕНИЕ? Примеры | МАТЕМАТИКА 5 классСкачать  Раскрытие скобок: правила, примеры, решенияРаскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач. Видео:Уравнения со скобками - 5 класс (примеры)Скачать  Что называется раскрытием скобок?Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2 · ( 3 + 4 ) на выражение вида 2 · 3 + 2 · 4 без скобок. Этот прием носит название раскрытия скобок. Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:
Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5 + ( − 3 ) − ( − 7 ) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок. Точно также мы можем заменить произведение выражений в скобках вида ( a + b ) · ( c + d ) на сумму a · c + a · d + b · c + b · d . Такой прием также не противоречит смыслу раскрытия скобок. Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x 2 · 1 a — x + sin ( b ) будет соответствовать выражение без скобок вида x 2 · 1 a — x 2 · x + x 2 · sin ( b ) . Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3 − ( 5 − 7 ) мы получаем выражение 3 − 5 + 7 . Оба этих выражения мы можем записать в виде равенства 3 − ( 5 − 7 ) = 3 − 5 + 7 . Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5 − ( 3 − ( 2 − 1 ) ) = 5 − ( 3 − 2 + 1 ) = 5 − 3 + 2 − 1 или 5 − ( 3 − ( 2 − 1 ) ) = 5 − 3 + ( 2 − 1 ) = 5 − 3 + 2 − 1 . Видео:Сложные уравнения. Как решить сложное уравнение?Скачать  Правила раскрытия скобок, примерыПриступим к рассмотрению правил раскрытия скобок. У одиночных чисел в скобкахОтрицательные числа в скобках часто встречаются в выражениях. Например, ( − 4 ) и 3 + ( − 4 ) . Положительные числа в скобках тоже имеют место быть. Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а , + ( а ) на + а , — ( а ) на – а . Если вместо а взять конкретное число, то согласно правилу: число ( 5 ) запишется как 5 , выражение 3 + ( 5 ) без скобок примет вид 3 + 5 , так как + ( 5 ) заменяется на + 5 , а выражение 3 + ( − 5 ) эквивалентно выражению 3 − 5 , так как + ( − 5 ) заменяется на − 5 . Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни. Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. + ( − a ) мы заменяем на − a , − ( − a ) заменяется на + a . Если выражение начинается с отрицательного числа ( − a ) , которое записано в скобках, то скобки опускаются и вместо ( − a ) остается − a . Приведем примеры: ( − 5 ) можно записать как − 5 , ( − 3 ) + 0 , 5 принимает вид − 3 + 0 , 5 , 4 + ( − 3 ) превращается в 4 − 3 , а − ( − 4 ) − ( − 3 ) после раскрытия скобок принимает вид 4 + 3 , так как − ( − 4 ) и − ( − 3 ) заменяется на + 4 и + 3 . Следует понимать, что записать выражение 3 · ( − 5 ) как 3 · − 5 нельзя. Об этом речь пойдет в следующих пунктах. Давайте посмотрим, на чем основываются правила раскрытия скобок. Согласно правилу разность a − b равна a + ( − b ) . На основе свойств действий с числами мы можем составить цепочку равенств ( a + ( − b ) ) + b = a + ( ( − b ) + b ) = a + 0 = a , которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + ( − b ) — это разность a − b . Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что − ( − a ) = a , a − ( − b ) = a + b . Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть − ( − ( ( − ( 5 ) ) ) ) . Раскроем скобки, продвигаясь изнутри наружу: − ( − ( ( − ( 5 ) ) ) ) = − ( − ( ( − 5 ) ) ) = − ( − ( − 5 ) ) = − ( 5 ) = − 5 . Также этот пример можно разобрать и в обратном направлении: − ( − ( ( − ( 5 ) ) ) ) = ( ( − ( 5 ) ) ) = ( − ( 5 ) ) = − ( 5 ) = − 5 . Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком « + » впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках. К примеру, после раскрытия скобок выражение − ( − 2 · x ) − ( x 2 ) + ( − 1 x ) − ( 2 · x · y 2 : z ) примет вид 2 · x − x 2 − 1 x − 2 · x · y 2 : z . Как мы это сделали? Мы знаем, что − ( − 2 · x ) есть + 2 · x , а так как это выражение стоит вначале, то + 2 · x можно записать как 2 · x , − ( x 2 ) = − x 2 , + ( − 1 x ) = − 1 x и − ( 2 · x · y 2 : z ) = − 2 · x · y 2 : z . В произведениях двух чиселНачнем с правила раскрытия скобок в произведении двух чисел. Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел − a и − b вида ( − a ) · ( − b ) мы можем заменить на ( a · b ) , а произведения двух чисел с противоположными знаками вида ( − a ) · b и a · ( − b ) заменить на ( − a · b ) . Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус. Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками. Рассмотрим несколько примеров. Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел — 4 3 5 и — 2 , вида ( — 2 ) · — 4 3 5 . Для этого заменим исходное выражение на 2 · 4 3 5 . Раскроем скобки и получим 2 · 4 3 5 . А если мы возьмем частное отрицательных чисел ( − 4 ) : ( − 2 ) , то запись после раскрытия скобок будет иметь вид 4 : 2 На месте отрицательных чисел − a и − b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п. Раскроем скобки в выражении — 3 · x x 2 + 1 · x · ( ln 5 ) . Согласно правилу, мы можем произвести следующие преобразования: — 3 · x x 2 + 1 · x · ( ln 5 ) = — 3 · x x 2 + 1 · x · ln 5 = 3 · x x 2 + 1 · x · ln 5 . Выражение ( − 3 ) · 2 можно преобразовать в выражение ( − 3 · 2 ) . После этого можно раскрыть скобки: − 3 · 2 . 2 3 · — 4 5 = — 2 3 · 4 5 = — 2 3 · 4 5 Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок: ( − 5 ) : 2 = ( − 5 : 2 ) = − 5 : 2 и 2 3 4 : ( — 3 , 5 ) = — 2 3 4 : 3 , 5 = — 2 3 4 : 3 , 5 . Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера. — 1 x + 1 : x — 3 = — 1 x + 1 : x — 3 = — 1 x + 1 : x — 3 sin ( x ) · ( — x 2 ) = ( — sin ( x ) · x 2 ) = — sin ( x ) · x 2 В произведениях трех и большего количества чиселПерейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус. Для примера, возьмем выражение 5 · ( − 3 ) · ( − 2 ) , которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как ( 5 · 3 · 2 ) и затем окончательно раскрыть скобки, получив выражение 5 · 3 · 2 . В произведении ( − 2 , 5 ) · ( − 3 ) : ( − 2 ) · 4 : ( − 1 , 25 ) : ( − 1 ) пять чисел являются отрицательными. поэтому ( − 2 , 5 ) · ( − 3 ) : ( − 2 ) · 4 : ( − 1 , 25 ) : ( − 1 ) = ( − 2 , 5 · 3 : 2 · 4 : 1 , 25 : 1 ) . Окончательно раскрыв скобки, получаем −2,5·3:2·4:1,25:1. Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и — 1 или — 1 заменяем на ( − 1 ) · a . Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные − 1 , в начало выражения. Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус. Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении — 2 3 : ( — 2 ) · 4 : — 6 7 выглядела бы следующим образом: — 2 3 : ( — 2 ) · 4 : — 6 7 = — 2 3 · — 1 2 · 4 · — 7 6 = = ( — 1 ) · 2 3 · ( — 1 ) · 1 2 · 4 · ( — 1 ) · 7 6 = = ( — 1 ) · ( — 1 ) · ( — 1 ) · 2 3 · 1 2 · 4 · 7 6 = ( — 1 ) · 2 3 · 1 2 · 4 · 7 6 = = — 2 3 · 1 2 · 4 · 7 6 Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение x 2 · ( — x ) : ( — 1 x ) · x — 3 : 2 . Его можно привести к выражению без скобок x 2 · x : 1 x · x — 3 : 2 . Раскрытие скобок, перед которыми стоит знак «+»Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение. Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс. Для примера приведем выражение ( 12 − 3 , 5 ) − 7 . Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид ( 12 − 3 , 5 ) − 7 = + 12 − 3 , 5 − 7 . В приведенном примере знак перед первым слагаемым ставить не обязательно, так как + 12 − 3 , 5 − 7 = 12 − 3 , 5 − 7 . Рассмотрим еще один пример. Возьмем выражение x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x и проведем с ним действия x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x = = x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x Вот еще один пример раскрытия скобок: 2 + x 2 + 1 x — x · y · z + 2 · x — 1 + ( — 1 + x — x 2 ) = = 2 + x 2 + 1 x — x · y · z + 2 · x — 1 — 1 + x + x 2 Как раскрываются скобки, перед которыми стоит знак минусРассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение. Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные. — — 1 2 = 1 2 , — 1 x + 1 = — 1 x + 1 , — ( — x 2 ) = x 2 Выражения с переменными могут быть преобразованы с использованием того же правила: — — x + x 3 — 3 — — 2 · x 2 + 3 · x 3 · x + 1 x — 1 — x + 2 , получаем x — x 3 — 3 + 2 · x 2 — 3 · x 3 · x + 1 x — 1 — x + 2 . Раскрытие скобок при умножении числа на скобку, выражения на скобкуЗдесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида ( a 1 ± a 2 ± … ± a n ) · b = ( a 1 · b ± a 2 · b ± … ± a n · b ) или b · ( a 1 ± a 2 ± … ± a n ) = ( b · a 1 ± b · a 2 ± … ± b · a n ) , где a 1 , a 2 , … , a n и b – некоторые числа или выражения. Например, проведем раскрытие скобок в выражении ( 3 − 7 ) · 2 . Согласно правилу, мы можем провести следующие преобразования: ( 3 − 7 ) · 2 = ( 3 · 2 − 7 · 2 ) . Получаем 3 · 2 − 7 · 2 . Раскрыв скобки в выражении 3 · x 2 · 1 — x + 1 x + 2 , получаем 3 x 2 · 1 — 3 · x 2 · x + 3 · x 2 · 1 x + 2 . Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать  Умножение скобки на скобкуРассмотрим произведение двух скобок вида ( a 1 + a 2 ) · ( b 1 + b 2 ) . Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку. Для того, чтобы решить приведенный пример, обозначим выражение ( b 1 + b 2 ) как b . Это позволит нам использовать правило умножения скобки на выражение. Получим ( a 1 + a 2 ) · ( b 1 + b 2 ) = ( a 1 + a 2 ) · b = ( a 1 · b + a 2 · b ) = a 1 · b + a 2 · b . Выполнив обратную замену b на ( b 1 + b 2 ) , снова применим правило умножения выражения на скобку: a 1 · b + a 2 · b = = a 1 · ( b 1 + b 2 ) + a 2 · ( b 1 + b 2 ) = = ( a 1 · b 1 + a 1 · b 2 ) + ( a 2 · b 1 + a 2 · b 2 ) = = a 1 · b 1 + a 1 · b 2 + a 2 · b 1 + a 2 · b 2 Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок. Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты. Формула будет иметь вид: ( a 1 + a 2 + . . . + a m ) · ( b 1 + b 2 + . . . + b n ) = = a 1 b 1 + a 1 b 2 + . . . + a 1 b n + + a 2 b 1 + a 2 b 2 + . . . + a 2 b n + + . . . + + a m b 1 + a m b 1 + . . . a m b n Проведем раскрытие скобок в выражении ( 1 + x ) · ( x 2 + x + 6 ) Оно представляет собой произведение двух сумм. Запишем решение: ( 1 + x ) · ( x 2 + x + 6 ) = = ( 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6 ) = = 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6 Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение ( 1 − x ) · ( 3 · x · y − 2 · x · y 3 ) . Сначала представим выражения в скобках в виде сумм: ( 1 + ( − x ) ) · ( 3 · x · y + ( − 2 · x · y 3 ) ) . Теперь мы можем применить правило: ( 1 + ( − x ) ) · ( 3 · x · y + ( − 2 · x · y 3 ) ) = = ( 1 · 3 · x · y + 1 · ( − 2 · x · y 3 ) + ( − x ) · 3 · x · y + ( − x ) · ( − 2 · x · y 3 ) ) Раскроем скобки: 1 · 3 · x · y − 1 · 2 · x · y 3 − x · 3 · x · y + x · 2 · x · y 3 . Видео:Раскрытие скобок. Преобразование буквенных выраженийСкачать  Раскрытие скобок в произведениях нескольких скобок и выраженийПри наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении ( 2 + 4 ) · 3 · ( 5 + 7 · 8 ) . В выражении содержится сразу три множителя ( 2 + 4 ) , 3 и ( 5 + 7 · 8 ) . Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: ( 2 + 4 ) · 3 · ( 5 + 7 · 8 ) = ( ( 2 + 4 ) · 3 ) · ( 5 + 7 · 8 ) . В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ( ( 2 + 4 ) · 3 ) · ( 5 + 7 · 8 ) = ( 2 · 3 + 4 · 3 ) · ( 5 + 7 · 8 ) . Умножаем скобку на скобку: ( 2 · 3 + 4 · 3 ) · ( 5 + 7 · 8 ) = 2 · 3 · 5 + 2 · 3 · 7 · 8 + 4 · 3 · 5 + 4 · 3 · 7 · 8 . Видео:Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать  Скобка в натуральной степениСтепени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок. Рассмотрим процесс преобразования выражения ( a + b + c ) 2 . Его можно записать в виде произведения двух скобок ( a + b + c ) · ( a + b + c ) . Произведем умножение скобки на скобку и получим a · a + a · b + a · c + b · a + b · b + b · c + c · a + c · b + c · c . Разберем еще один пример: 1 x + 2 3 = 1 x + 2 · 1 x + 2 · 1 x + 2 = = 1 x · 1 x + 1 x · 2 + 2 · 1 x + 2 · 2 · 1 x + 2 = = 1 x · 1 x · 1 x + 1 x · 2 · 1 x + 2 · 1 x · 1 x + 2 · 2 · 1 x + 1 x · 1 x · 2 + + 1 x 2 · 2 + 2 · 1 x · 2 + 2 · 2 · 2 Видео:Как быстро раскрывать скобкиСкачать  Деление скобки на число и скобки на скобкуДеление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, ( x 2 — x ) : 4 = x 2 : 4 — x : 4 . Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку. Например, нам необходимо раскрыть скобки в выражении ( x + 2 ) : 2 3 . Для этого сначала заменим деление умножением на обратное число ( x + 2 ) : 2 3 = ( x + 2 ) · 2 3 . Умножим скобку на число ( x + 2 ) · 2 3 = x · 2 3 + 2 · 2 3 . Вот еще один пример деления на скобку: 1 x + x + 1 : ( x + 2 ) . Заменим деление умножением: 1 x + x + 1 · 1 x + 2 . Выполним умножение: 1 x + x + 1 · 1 x + 2 = 1 x · 1 x + 2 + x · 1 x + 2 + 1 · 1 x + 2 . Видео:РАСКРЫТИЕ СКОБОК В УРАВНЕНИИ. Примеры | МАТЕМАТИКА 6 классСкачать  Порядок раскрытия скобокТеперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени. Порядок выполнения действий:
Рассмотрим порядок выполнения действий на примере выражения ( − 5 ) + 3 · ( − 2 ) : ( − 4 ) − 6 · ( − 7 ) . Намнем преобразование с выражений 3 · ( − 2 ) : ( − 4 ) и 6 · ( − 7 ) , которые должны принять вид ( 3 · 2 : 4 ) и ( − 6 · 7 ) . При подстановке полученных результатов в исходное выражение получаем: ( − 5 ) + 3 · ( − 2 ) : ( − 4 ) − 6 · ( − 7 ) = ( − 5 ) + ( 3 · 2 : 4 ) − ( − 6 · 7 ) . Раскрываем скобки: − 5 + 3 · 2 : 4 + 6 · 7 . Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу. 🎦 ВидеоРаскрытие скобок и приведение подобных слагаемых. 6 класс.Скачать  |