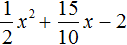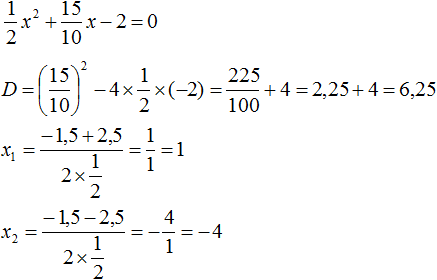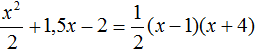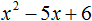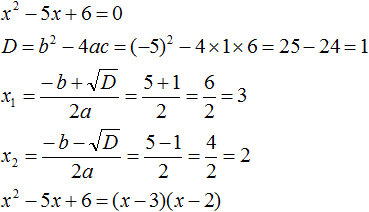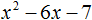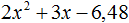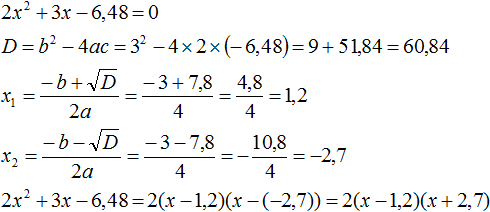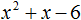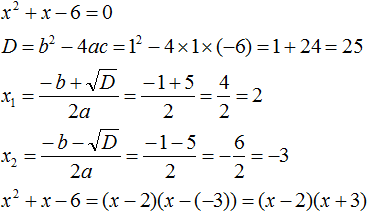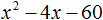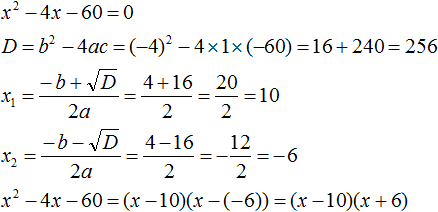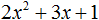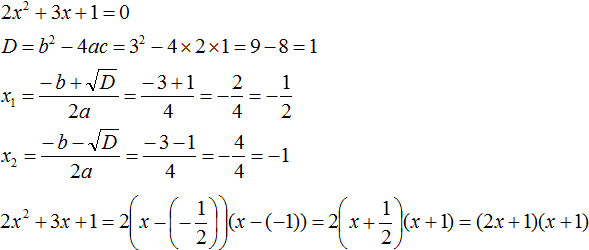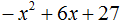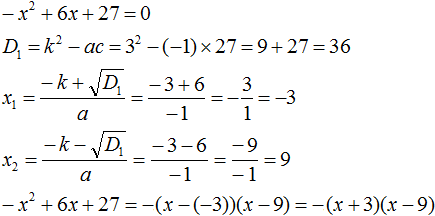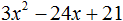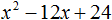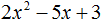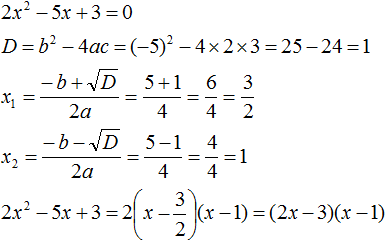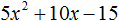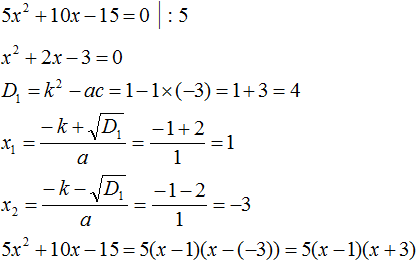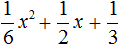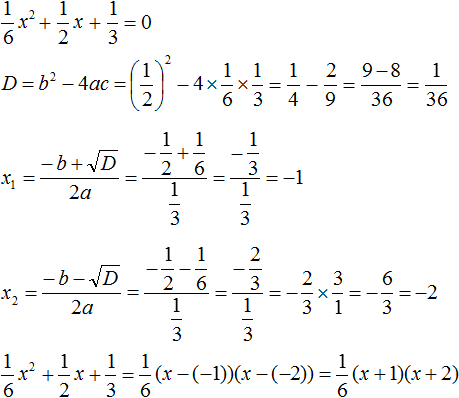Неполное квадратное уравнение – это уравнение вида
в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид:
| ax 2 + bx = 0, | если c = 0; |
| ax 2 + c = 0, | если b = 0; |
| ax 2 = 0, | если b = 0 и c = 0. |
- Решение неполных квадратных уравнений
- Неполные квадратные уравнения
- Основные понятия
- Решение неполных квадратных уравнений
- Как решить уравнение ax² = 0
- Как решить уравнение ax² + с = 0
- В двух словах
- Как решить уравнение ax² + bx = 0
- Разложение квадратного трёхчлена на множители
- Как разложить на множители квадратный трёхчлен
- Как это работает
- Примеры разложений
- Задания для самостоятельного решения
- 📸 Видео
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Решение неполных квадратных уравнений
Чтобы решить уравнение вида ax 2 + bx = 0 , надо разложить левую часть уравнения на множители, вынеся x за скобки:
Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит:
Чтобы ax + b было равно нулю, нужно, чтобы
| x = — | b | . |
| a |
Следовательно, уравнение ax 2 + bx = 0 имеет два корня:
| x1 = 0 и x2 = — | b | . |
| a |
Неполные квадратные уравнения вида ax 2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю.
Пример 1. Решите уравнение:
| a 2 — 12a = 0 | |
| a(a — 12) = 0 | |
| a1 = 0 | a — 12 = 0 |
| a2 = 12 | |
Пример 2. Решите уравнение:
| 7x 2 = x | |
| 7x 2 — x = 0 | |
| x(7x — 1) = 0 |
| x1 = 0 | 7x — 1 = 0 | ||
| 7x = 1 | |||
|
Чтобы решить уравнение вида ax 2 + c = 0 , надо перенести свободный член уравнения c в правую часть:
| ax 2 = —c, следовательно, x 2 = — | c | . |
| a |
В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа.
Если данное неполное уравнение будет иметь вид x 2 — c = 0 , то сначала опять переносим свободный член в правую часть и получаем:
В этом случае уравнение будет иметь два противоположных корня:
Неполное квадратное уравнение вида ax 2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами.
Пример 1. Решите уравнение:
| 24 = 2y 2 | |
| 24 — 2y 2 = 0 | |
| -2y 2 = -24 | |
| y 2 = 12 | |
| y1 = +√ 12 | y2 = -√ 12 |
Пример 2. Решите уравнение:
| b 2 — 16 = 0 | |
| b 2 = 16 | |
| b1 = 4 | b2 = -4 |
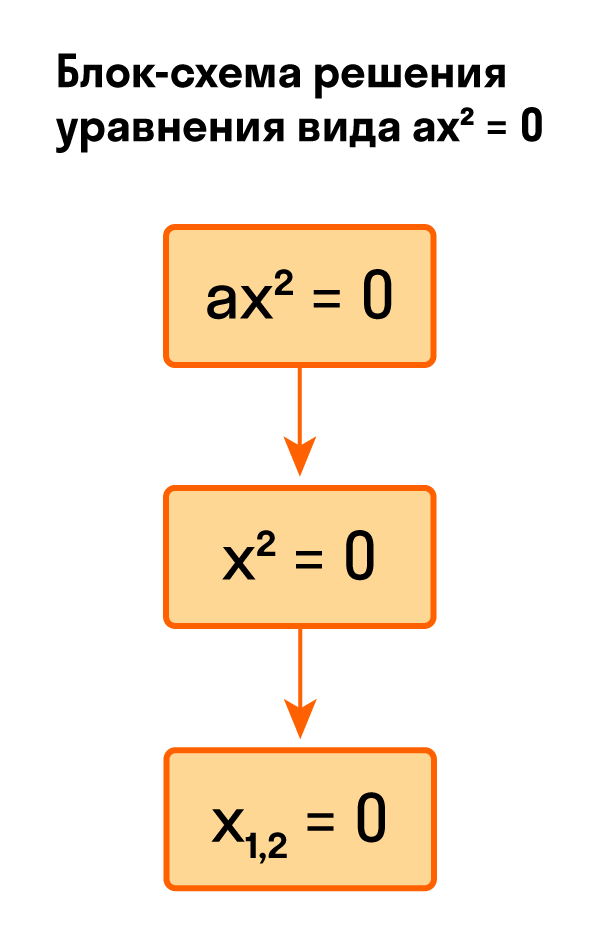
Уравнение вида ax 2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax 2 = 0 следует, что x 2 = 0, значит, и x = 0. Любое другое значение x не будет являться корнем данного уравнения.
Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать
Неполные квадратные уравнения
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать
Основные понятия
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
Неполные квадратные уравнения бывают трех видов:
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать  Решение неполных квадратных уравненийКак мы уже знаем, есть три формулы неполных квадратных уравнений:
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль). Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать  Как решить уравнение ax² = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0. Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0. Пример 1. Решить −5x² = 0.
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса! Видео:АЛГЕБРА 8 класс : Решение неполных квадратных уравнений | ВидеоурокСкачать  Как решить уравнение ax² + с = 0Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней. В двух словахНеполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
Пример 1. Найти решение уравнения 9x² + 4 = 0.
Разделим обе части на 9: Ответ: уравнение 9x² + 4 = 0 не имеет корней. Пример 2. Решить -x² + 9 = 0.
Разделим обе части на -1: Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3. Видео:Математика| Разложение квадратного трехчлена на множители.Скачать  Как решить уравнение ax² + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника. Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: Пример 1. Решить уравнение 2x² — 32x = 0
Ответ: х = 0 и х = 16. Пример 2. Решить уравнение 3x² — 12x = 0 Разложить левую часть уравнения на множители и найти корни: Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать  Разложение квадратного трёхчлена на множителиВидео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать  Как разложить на множители квадратный трёхчленКвадратный трёхчлен — это многочлен вида ax 2 + bx + c . В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так: Левая часть этого уравнения является квадратным трёхчленом. Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена. Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением: Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой: Где левая часть — исходный квадратный трёхчлен. Пример 1. Разложить на множители следующий квадратный трёхчлен: Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение: В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Итак, x1 = 6 , x2 = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x1)(x − x2). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x1 = 6, x2 = 2 Если a равно единице (как в данном примере), то решение можно записать покороче: Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства. Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12 Пример 2. Разложить на множители следующий квадратный трёхчлен: Приравняем данный квадратный трёхчлен к нулю и решим уравнение: Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Итак, x1 = 4 , x2 = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x1)(x − x2) , где вместо переменных a , x1 и x2 подстáвим соответствующие значения. В данном случае a = 2 Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24 Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать  Как это работаетРазложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования. Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице: Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x1 + x2 = −b . Для этого можно умножить обе его части на −1
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x2
Далее замечаем, что выражение ( x − x1 ) является общим множителем. Вынесем его за скобки:
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить. Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1
Теперь из второго равенства выразим c . Для этого умножим обе его части на a
Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:
Здесь вместо переменных b и c были подставлены выражения −ax1 − ax2 и ax1x2 , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax2
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:
Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x1)(x − x2) вместо переменных x1 и x2 . Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x1 и x2 . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2
Тогда значение −2 в процессе разложения на множители будет подставлено вместо x1 и x2 . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Видео:Неполные квадратные уравненияСкачать  Примеры разложенийПример 1. Разложить на множители следующий квадратный трёхчлен: Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x1)(x − x2) , где вместо a , x1 и x2 подстáвим соответствующие значения:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен: Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим: Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен: Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2) Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x1
Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета. В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Теперь из второго равенства выразим k . Так мы найдём его значение.
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Видео:РЕШЕНИЕ НЕПОЛНОГО КВАДРАТНОГО УРАВНЕНИЯ ЗА 5 СЕКУНДСкачать  Задания для самостоятельного решения
Понравился урок? Возникло желание поддержать проект? 📸 ВидеоНЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ 8 классСкачать  8 кл. Решение неполных квадратных уравнений.Скачать  Алгебра 8 класс (Урок№27 - Квадратные уравнения. Неполные квадратные уравнения.)Скачать  Как решать неполное квадратное уравнение? 😎Скачать  КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать  5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать  Метод выделения полного квадрата. 8 класс.Скачать  Квадратные уравнения #shorts Как решать квадратные уравненияСкачать  |
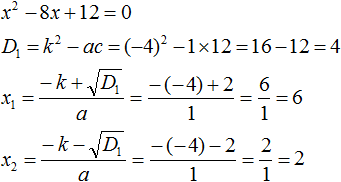
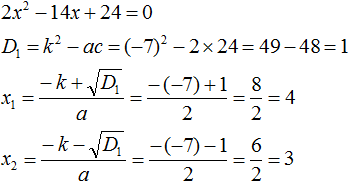
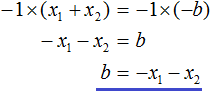
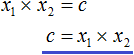
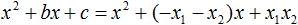
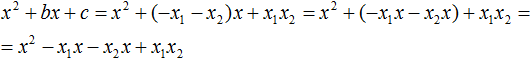
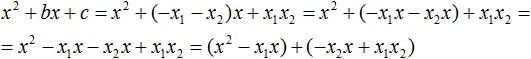
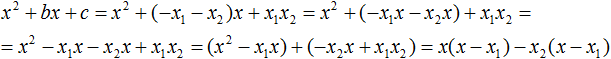
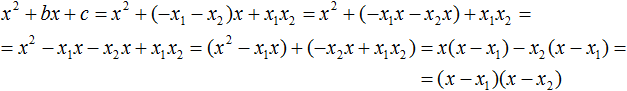
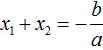и 
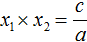
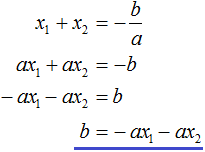
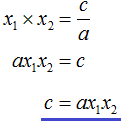
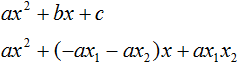
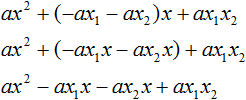
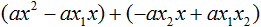
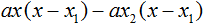
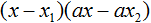
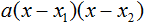
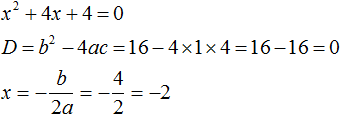
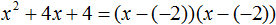
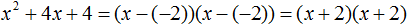
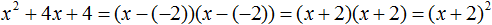
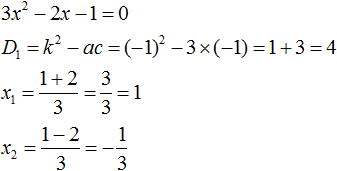
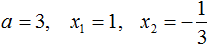
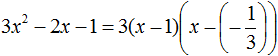
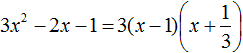
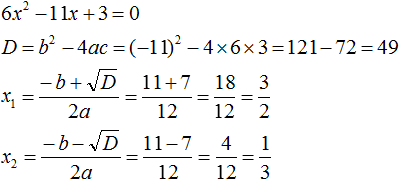
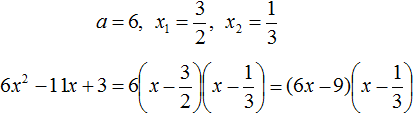
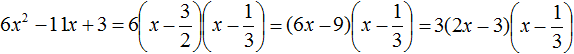
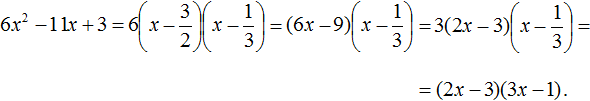
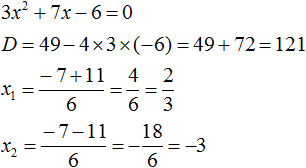
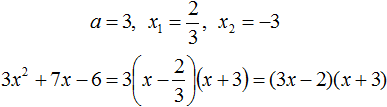
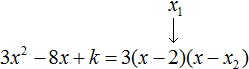
, а произведение корней — дроби 
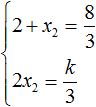
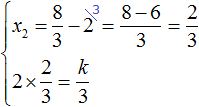
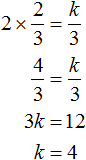
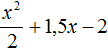
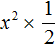. Если поменять местами сомножители, то получится 
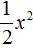. То есть коэффициент a станет равным 
