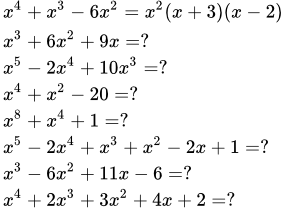Как раскладывать на множители биквадратное уравнение (3 видео)

Решение уравнений, сводящихся к квадратным

Содержание

Биквадратные уравнения
Метод разложения на множители
Метод замены переменной
Выделение полного квадрата
Примеры
Примеры разложения многочленов на множители
Примеры с решением квадратного уравнения
Пример 1.1
Пример 1.2
Пример 1.3
Примеры разложения многочленов на множители с помощью формул
Примеры с биквадратными многочленами
Пример 2.1
Пример 2.2
Пример 2.3 с возвратным многочленом
Примеры разложения многочленов на множители с целыми корнями
Пример 3.1
Пример 3.2
Биквадратное уравнение. Алгоритм решения и примеры.
Формула биквадратного уравнения:
Как решаются биквадратные уравнения?
📹 Видео

Биквадратные уравнения

Биквадратным уравнением называется уравнение вида:

$$ ax^4+bx^2+c = 0, a neq 0 $$

Алгоритм решения биквадратного уравнения

Шаг 1. Ввести новую переменную: $z = x^2 ge 0$.

Переписать уравнение для новой переменной: $az^2+bz+c = 0$

Шаг 2. Решить полученное квадратное уравнение.

Если $D gt 0$, $z_ = frac<-b pm sqrt> $. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.

Если D = 0,$z_0 = -frac$. Проверить условие $z ge 0$, если корень отрицательный, решений нет, переход на шаг 4.

Если $D lt 0$, решений нет, переход на шаг 4.

Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = pm sqrt$.

Шаг 4. Работа завершена.

Шаг 1. $z = x^2 ge 0, z^2+7z-30 = 0$

$z_1 = -10 lt 0, z_2 = 3 gt 0 $

Шаг 3. Находим корни из положительного $z: x_ = pm sqrt$

Метод разложения на множители

Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.

Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.

Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.

Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.

Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.

При разложении многочлена

множители вида (x-a) называют линейными множителями ;
множители вида $ (x^2+bx+c)$, для которых $D lt 0$, называют неприводимыми квадратичными множителями .

Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.

Причём, такое представление единственно с точностью до порядка множителей.

Для разложения многочленов на множители применяются разные методы:

вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
группировка (см. §20 справочника для 7 класса);
формулы сокращенного умножения (см. §25 справочника для 7 класса);
метод неопределённых коэффициентов;
выделение полного квадрата и т.п.

Решим уравнение $2x^3-x^2-8x+4 = 0$.

Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$

$$ (x^2-4)(2x-1) = 0 Rightarrow (x-2)(x+2)(2x-1) = 0 $$

Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = frac$

Метод замены переменной

Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:

$Исходное quad сложное quad уравнение iff <left< begin Новая quad переменная quad (урав. quad связи quad со quad старой quad переменной \ Исходное quad урав. quad в quad «упрощ.» quad виде end right.>$

Например, для биквадратных уравнений:

$$ ax^4+bx^2+c = 0 iff <left< begin z = x^2 ge 0 \ az^2+bz+c = 0 end right.> $$

Можно предложить аналогичные схемы для других уравнений:

$$ ax+b sqrt+c = 0 iff <left< begin z = sqrt ge 0 \ az^2+bz+c = 0 end right.> $$

И, в общем виде, для любой рациональной степени n:

$$ ax^+bx^n+c = 0 iff <left< begin z = x^n \ az^2+bz+c = 0 end right.> , n in Bbb Q $$

В других случаях замена переменной не настолько очевидна.

Но при удачном выборе, этот метод очень упрощает задачу.

Раскроем скобки:$ x^2-x = frac$. Сделаем замену:

$$ z = frac Rightarrow z(z-2) = 24 Rightarrow z^2-2z-24 = 0 Rightarrow (z-6)(z+4) = 0 Rightarrow left[ begin z_1 = -4 \ z_2 = 6 end right.$$

Возвращаемся к исходной переменной x:

$$ left[ begin x^2-x = -4 \ x^2-x = 6 end right. Rightarrow left[ begin x^2-x+4 = 0 \ x^2-x-6 = 0 end right. Rightarrow left[ begin D lt 0, x in varnothing \ (x-3)(x+2) = 0 end right. Rightarrow left[ begin x_1 = -2 \ x_2 = 3 end right. $$

При использовании метода замены переменной не забывайте возвращаться к исходной переменной.

Выделение полного квадрата

Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:

$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$

Такое разложение не всегда возможно.

Рассмотрим выделение полного квадрата для квадратного трёхчлена:

$$ = a Biggl(x+frac Biggr)^2 — frac = a Biggl(x+ frac Biggr)^2- frac, D = b^2-4ac $$

Нами выделен полный квадрат $(x+frac)^2$.

Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).

А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D ge 0$.

Решить уравнение $x^4+4x^2-1 = 0$

Выделим полный квадрат и разложим на множители:

$$ left[ begin x^2+2-sqrt = 0 \ x^2+2+sqrt = 0 end right. Rightarrow left[ begin x^2 = sqrt -2 gt 0 \ x^2 = -(2+sqrt) lt 0 end right. Rightarrow x_1,2 = pm sqrt<sqrt-2> $$

Примеры

Пример 1. Решите биквадратные уравнения:

Делаем замену: $2x^4+7x^2-4 = 0 iff <left< begin z = x^2 ge 0 \ 2z^2+7z-4 = 0 end right.>$

Решаем квадратное уравнение: $D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2$

$$ z = frac = left[ begin z_1 = -4 lt 0 \ z_2 = frac gt 0 end right. $$

Выбираем положительный z и возвращаемся к исходной переменной x:

Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 iff <left< begin z = (x+3)^2 ge 0 \ z^2-10z+24 = 0 end right.>$

Решаем квадратное уравнение: $z^2-10z+24 = 0 Rightarrow (z-4)(z-6) = 0 Rightarrow left[ begin z_1 = 4 \ z_2 = 6 end right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ left[ begin (x+3)^2 = 4 \ (x+3)^2 = 6 end right. Rightarrow left[ begin x+3 = pm sqrt \ x+3 = pm sqrt end right. Rightarrow left[ begin x_ = -3 pm 2 \ x_ = -3 pm sqrt end right. Rightarrow left[ begin x_1 = -5 \ x_2 = -1 \ x_ = -3 pm sqrt end right. $$

Пример 2. Решите уравнения аналогичные биквадратным:

Делаем замену: $x+4 sqrt-60 = 0 iff <left< begin z = sqrt ge 0 \ z^2+4z-60 = 0 end right.>$

Решаем квадратное уравнение: $ z^2+4z-60 = 0 Rightarrow (z+10)(z-6) = 0 Rightarrow left[ begin z_1 = -10 \ z_2 = 6 end right.$

Выбираем положительный корень и возвращаемся к исходной переменной:

Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 iff <left< begin z = (x-1)^3 \ z^2-7z-8 = 0 end right.>$

Решаем квадратное уравнение: $ z^2-7z-8 = 0 Rightarrow (z+1)(z-8) = 0 Rightarrow left[ begin z_1 = -1 \ z_2 = 8 end right.$

При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.

$$ left[ begin (x-1)^3 = -1 \ (x-1)^3 = 8 end right. Rightarrow left[ begin x-1 = -1 \ x-1 = 2 end right. Rightarrow left[ begin x_1 = 0 \ x_2 = 3 end right. $$

Пример 3. Решите уравнения с помощью замены переменной:

Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:

$$ (x^2+6x)^2-(x^2+6x+9) = 33 Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$

Решаем квадратное уравнение: $ z^2-z-42 = 0 Rightarrow (z+6)(z-7) = 0 Rightarrow left[ begin z_1 = -6 \ z_2 = 7 end right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ left[ begin x^2+6x = -6 \ x^2+6x = 7 end right. Rightarrow left[ begin x^2+6x+6 = 0 \ x^2+6x-7=0 end right. Rightarrow left[ begin D = 12, x = frac<-6 pm 2 sqrt> \ (x+7)(x-1) = 0 end right. Rightarrow left[ begin x_ = -3 pm sqrt \ x_3 = -7 \ x_4 = 1 end right. $$

Делаем замену: $ frac + frac = 2 iff left[ begin z = x^2+3 ge 3 \ frac + frac = 2 end right.$

Решаем уравнение относительно z:

$$ frac + frac = 2 Rightarrow frac = frac Rightarrow 4(z+1)+5z = 2z(z+1) $$

$$ 2z^2+2z-9z-4 = 0 Rightarrow 2z^2-7z-4 = 0 $$

$$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $$

$$ z = frac = left[ begin z_1 = — frac lt 3 \ z_2 = 4 gt 3 end right. $$

Выбираем корень больше 3 и возвращаемся к исходной переменной:

$$ x^2+3 = 4 Rightarrow x^2 = 1 Rightarrow x_ = pm 1$$

Пример 4*. Решите уравнения:

Приведём это уравнение к биквадратному.

В линейных множителях (x+a) выберем все a =

Найдем их среднее арифметическое (см. §52 справочника для 7 класса)

Замена переменных $z = x+a_$:

Упрощаем уравнение, используя формулу разности квадратов:

$$ (z^2-9)(z^2-1) = 945 Rightarrow z^4-10z^2+9 = 945 Rightarrow z^4-10z^2-936 = 0 $$

Получили биквадратное уравнение.

Делаем замену: $z^4-10z^2-936 = 0 iff <left< begin t = z^2 ge 0 \ t^2-10t-936 = 0 end right.> $

Решаем квадратное уравнение:

$$ D = 100+4 cdot 936 = 3844 = 62^2, t = frac = left[ begin t_1 = -26 lt 0 \ t_2 = 36 gt 0 end right. $$

Выбираем положительный корень и возвращаемся к переменной z:

$$ z = pm sqrt = pm sqrt = pm 6 $$

Возвращаемся к исходной переменной x:

$$ x = z-4 = pm 6-4 = left[ begin x_1 = -10 \ x_2 = 2 end right. $$

$$ z- frac =2,1 |times z (z neq 0) $$

$$ z^2-2,1z-1 = 0 Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = frac = left[ begin z_1 = -0,4 \ z_2 = 2,5 end right. $$

Берём оба корня и возвращаемся к исходной переменной.

$$ left[ begin frac = -0,4 \ frac = 2,5 end right. Rightarrow left[ begin x^2+1 = -0,4x \x^2+1 = 2,5x end right. Rightarrow left[ begin x^2+0,4x+1 = 0 \ x^2-2,5x+1 = 0 end right. $$

В первом уравнении $D = 0,4^2-4 lt 0$, решений нет.

Во втором уравнении (x-2)(x-1/2) = 0 $Rightarrow left[ begin x_1 = frac \ x_2 = 2 end right.$

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Примеры разложения многочленов на множители

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Примеры с решением квадратного уравнения

Пример 1.1

Разложить многочлен на множители:
x 4 + x 3 – 6 x 2 .

Выносим x 2 за скобки:
.
Решаем квадратное уравнение x 2 + x – 6 = 0 :
.
Корни уравнения:
, .

Отсюда получаем разложение многочлена на множители:
.

Пример 1.2

Разложить на множители многочлен третьей степени:
x 3 + 6 x 2 + 9 x .

Выносим x за скобки:
.
Решаем квадратное уравнение x 2 + 6 x + 9 = 0 :
Его дискриминант: .
Поскольку дискриминант равен нулю, то корни уравнения кратные: ;
.

Отсюда получаем разложение многочлена на множители:
.

Пример 1.3

Разложить на множители многочлен пятой степени:
x 5 – 2 x 4 + 10 x 3 .

Выносим x 3 за скобки:
.
Решаем квадратное уравнение x 2 – 2 x + 10 = 0 .
Его дискриминант: .
Поскольку дискриминант меньше нуля, то корни уравнения комплексные: ;
, .

Разложение многочлена на множители имеет вид:
.

Если нас интересует разложение на множители с действительными коэффициентами, то:
.

Видео:Разложение кубических выражений на множителиСкачать

Примеры разложения многочленов на множители с помощью формул

Примеры с биквадратными многочленами

Пример 2.1

Разложить биквадратный многочлен на множители:
x 4 + x 2 – 20 .

Применим формулы:
a 2 + 2 ab + b 2 = ( a + b ) 2 ;
a 2 – b 2 = ( a – b )( a + b ) .

;
.

Пример 2.2

Разложить на множители многочлен, сводящийся к биквадратному:
x 8 + x 4 + 1 .

Применим формулы:
a 2 + 2 ab + b 2 = ( a + b ) 2 ;
a 2 – b 2 = ( a – b )( a + b ) :

;

;
.

Пример 2.3 с возвратным многочленом

Разложить на множители возвратный многочлен:
.

Возвратный многочлен имеет нечетную степень. Поэтому он имеет корень x = – 1 . Делим многочлен на x – (–1) = x + 1 . В результате получаем:
.
Делаем подстановку:
, ;
;

;
.

Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Примеры разложения многочленов на множители с целыми корнями

Пример 3.1

Разложить многочлен на множители:
.

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x ). То есть целый корень может быть одним из чисел:
–6, –3, –2, –1, 1, 2, 3, 6 .
Подставляем поочередно эти значения:
(–6) 3 – 6·(–6) 2 + 11·(–6) – 6 = –504 ;
(–3) 3 – 6·(–3) 2 + 11·(–3) – 6 = –120 ;
(–2) 3 – 6·(–2) 2 + 11·(–2) – 6 = –60 ;
(–1) 3 – 6·(–1) 2 + 11·(–1) – 6 = –24 ;
1 3 – 6·1 2 + 11·1 – 6 = 0 ;
2 3 – 6·2 2 + 11·2 – 6 = 0 ;
3 3 – 6·3 2 + 11·3 – 6 = 0 ;
6 3 – 6·6 2 + 11·6 – 6 = 60 .

Итак, мы нашли три корня:
x ₁ = 1 , x ₂ = 2 , x ₃ = 3 .
Поскольку исходный многочлен – третьей степени, то он имеет не более трех корней. Поскольку мы нашли три корня, то они простые. Тогда
.

Пример 3.2

Разложить многочлен на множители:
.

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
–2, –1, 1, 2 .
Подставляем поочередно эти значения:
(–2) 4 + 2·(–2) 3 + 3·(–2) 3 + 4·(–2) + 2 = 6 ;
(–1) 4 + 2·(–1) 3 + 3·(–1) 3 + 4·(–1) + 2 = 0 ;
1 4 + 2·1 3 + 3·1 3 + 4·1 + 2 = 12 ;
2 4 + 2·2 3 + 3·2 3 + 4·2 + 2 = 54 .

Итак, мы нашли один корень:
x ₁ = –1 .
Делим многочлен на x – x ₁ = x – (–1) = x + 1 :

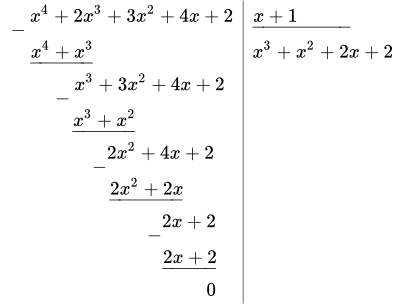
Тогда,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, –1, –2 .
Подставим x = –1 :
.

Итак, мы нашли еще один корень x ₂ = –1 . Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.

Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то разложение многочлена на множители имеет вид:
.

Автор: Олег Одинцов . Опубликовано: 18-06-2015

Видео:Схема Горнера. 10 класс.Скачать

Биквадратное уравнение. Алгоритм решения и примеры.

Биквадратные уравнения относятся к разделу школьной алгебры. Метод решения таких уравнений довольно простой, нужно использовать замену переменной.
Рассмотрим алгоритм решения:
-Что такое биквадратное уравнение?
-Как решить биквадратное уравнение?
-Метод замены переменной.
-Примеры биквадратного уравнения.
-Нахождение корней биквадратного уравнения.

Видео:Теорема Безу и разложение многочлена на множителиСкачать

Формула биквадратного уравнения:

Формулы биквадратного уравнения отличается от квадратного уравнения тем, что у переменной х степени повышатся в два раза.

ax 4 +bx 2 +c=0, где a≠0

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Как решаются биквадратные уравнения?

Решение биквадратных уравнений сводится сначала к замене, а потом решению квадратного уравнения:
(x^=t,;tgeq0)
t должно быть положительным числом или равным нулю

Получаем квадратное уравнение и решаем его:
at 2 +bt+c=0,
где x и t — переменная,
a, b, c -числовые коэффициенты.

(t^-5t+6=0)
Получилось полное квадратное уравнение, решаем его через дискриминант:
(D=b^-4ac=(-5)^-4times1times6=25-24=1)
Дискриминант больше нуля, следовательно, два корня, найдем их:

Возвращаемся в замену, подставим вместо переменной t полученные числа: (x^=3)
Чтобы решить такого вида уравнение, необходимо обе части уравнения занести под квадратный корень.

Получилось полное квадратное уравнение, решаем через дискриминант:
(D=b^-4ac=(-4)^-4times1times4=16-16=0)
Дискриминант равен нулю, следовательно, один корень, найдем его:
(t=frac=frac=2)

Возвращаемся в замену, подставим вместо переменной t полученное число:

Можно не во всех случаях делать замену. Рассмотрим пример.

Пример №3:
Решить биквадратное уравнение.

Выносим переменную x 2 за скобку,

Приравниваем каждый множитель к нулю

Делим всё уравнение на -4:
Чтобы решить (x^=4) такое уравнение, необходимо, обе части уравнения занести под квадратный корень.
(begin
&x^=4\
&x_=2\
&x_=-2\
end)

Пример №4:
Решите биквадратное уравнение.
(x^-16=0)

Возвращаемся в замену, подставим вместо переменной t полученное число:
(begin
&x^=4\
&x_=2\
&x_=-2
end)

Ответ: решения нет.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.